passons à une première expression de

avec trois fonctions de
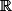
vers
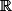
inconnues

,

et

Un petit calcul d'une dérivée (dérivée d'une fonction racine carrée donc du niveau première) (voir avant dernier post : les deux dernières équations avec les réels
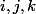
selon
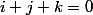
)
permet une première écriture de
)
en utilisant trois fonctions

,

et

et ici
=-i(x)-j(x))
donc
)
et
)
qui resteront à écrire pour conclure
ici la variable réelle

correspond à l'angle orienté

de la figure du post précédent
et ces trois fonctions correspondent aux trois réels
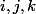
de l'avant dernier post
alors l'expression de

écriture sur trois lignes
=3-\frac {3}{2}.<br />\frac {b^2\begin {pmatrix}j(x)+3k(x) \end {pmatrix}+c^2\begin {pmatrix}3j(x)+k(x) \end {pmatrix}-a^2\begin {pmatrix} j(x)+k(x)\end {pmatrix}}{\sqrt {2b^2+2c^2-a^2}})
+3k(x) \end {pmatrix}+c^2\begin {pmatrix}3i(x)+k(x) \end {pmatrix}-b^2\begin {pmatrix} i(x)+k(x)\end {pmatrix}}{\sqrt {2a^2+2c^2-b^2}})
+3j(x) \end {pmatrix}+b^2\begin {pmatrix}3i(x)+j(x) \end {pmatrix}-c^2\begin {pmatrix} i(x)+j(x)\end {pmatrix}}{\sqrt {2a^2+2b^2-c^2}})
il ne reste plus qu'à écrire les fonctions

et

elles ne seront pas très jolies car le point

donné au second post n'est pas joli
Cordialement
yavlory



