Fonction continue sur les rationnels
11 messages
- Page 1 sur 1
fonction continue sur les rationnels
Bonjour, petit exo pour la route, existe-t-il une fonction continue sur  et discontinue sur
et discontinue sur 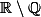 ?
?
Re: fonction continue sur les rationnels
Non, l'ensemble des points de continuité d'une fonction est toujours un 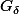 et
et  n'est pas un
n'est pas un 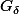 (
(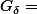 intersection dénombrable d'ouverts).
intersection dénombrable d'ouverts).
Re: fonction continue sur les rationnels
Montrons que l'ensemble des points de continuité d'une fonction est toujours une intersection dénombrable d'ouverts.
Soit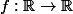 . Pour
. Pour 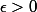 , on pose
, on pose
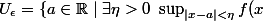 -\inf_{|x-a|<\eta}f(x) <\epsilon\})
(où les sup et inf sont pris dans la droite numérique achevée). Alors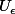 est ouvert pour tout
est ouvert pour tout 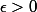 , et l'ensemble des points de continuité de
, et l'ensemble des points de continuité de  est l'intersection des
est l'intersection des 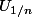 pour
pour  entier
entier 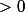 .
.
Supposons que soit l'ensemble des points de continuité d'une fonction. D'après ce qui précède,
soit l'ensemble des points de continuité d'une fonction. D'après ce qui précède,  devrait être une intersection dénombrable d'ouverts, et ces ouverts seraient tous denses puisqu'ils contiennent
devrait être une intersection dénombrable d'ouverts, et ces ouverts seraient tous denses puisqu'ils contiennent  . Par ailleurs
. Par ailleurs 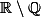 est une intersection d'ouverts denses (tous les
est une intersection d'ouverts denses (tous les 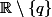 pour
pour 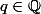 ). Donc on devrait avoir
). Donc on devrait avoir 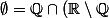) intersection dénombrable d'ouverts denses. Monsieur Baire se retourne dans sa tombe !
intersection dénombrable d'ouverts denses. Monsieur Baire se retourne dans sa tombe !
[C'est en général assez désopilant de regarder le forum Dlz9, par exemple ici. Le petit clown qui écrit dans ce message devrait apprendre à lire et à ne pas faire des citations fausses.
PS. Notre petit clown persiste. Il est victime d'hallucinations, il voit des "dense" qui n'y sont pas. Il est coutumier du fait, lire de travers est une habitude chez lui.
Ce qui est aussi une habitude chez lui, c'est d'être incapable de comprendre une démonstration, comme celle ci-dessus (d'ailleurs très classique, on peut en retrouver les éléments dans les pages wikipedia)]
Soit
(où les sup et inf sont pris dans la droite numérique achevée). Alors
Supposons que
[C'est en général assez désopilant de regarder le forum Dlz9, par exemple ici. Le petit clown qui écrit dans ce message devrait apprendre à lire et à ne pas faire des citations fausses.
PS. Notre petit clown persiste. Il est victime d'hallucinations, il voit des "dense" qui n'y sont pas. Il est coutumier du fait, lire de travers est une habitude chez lui.
Ce qui est aussi une habitude chez lui, c'est d'être incapable de comprendre une démonstration, comme celle ci-dessus (d'ailleurs très classique, on peut en retrouver les éléments dans les pages wikipedia)]
Modifié en dernier par GaBuZoMeu le 16 Aoû 2019, 17:42, modifié 1 fois.
Re: fonction continue sur les rationnels
Merci pour la démo du fait que l'ensemble des points de continuité est un 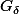 , curieusement ça fait partie de ces propriétés que je connais mais que j'ai toujours un mal fou à redémontrer. Je saurai où regarder la prochaine fois que j'oublie !
, curieusement ça fait partie de ces propriétés que je connais mais que j'ai toujours un mal fou à redémontrer. Je saurai où regarder la prochaine fois que j'oublie !
Re: fonction continue sur les rationnels
Le petit clown insiste. Puisqu'il ne comprend pas la démonstration, il fait maintenant semblant de croire que l'énigme posée par Tuvasbien est "existe-t-il une fonction dont la restriction à  est continue et la restriction à
est continue et la restriction à 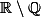 est discontinue ". Ce n'est bien sûr pas du tout ce que Tuvasbien demande, et il suffit de voir ce qu'il écrit d'habitude pour comprendre qu'il ne poserait une question aussi bêbête.
est discontinue ". Ce n'est bien sûr pas du tout ce que Tuvasbien demande, et il suffit de voir ce qu'il écrit d'habitude pour comprendre qu'il ne poserait une question aussi bêbête. 
Re: fonction continue sur les rationnels
Je confirme que la réponse est non et que GaBuZoMeu a bien compris la question contrairement à Dattier (désolé il ne pouvait y avoir qu'une seule bonne réponse sur ce coup-là). Pour ma part j'ai également utilisé le lemme de Baire et mon argument est identique au sien : si une telle fonction existait alors 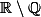 serait une réunion dénombrable de fermés et par suite
serait une réunion dénombrable de fermés et par suite  également (
également (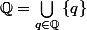 ), le lemme de Baire assurerait alors que
), le lemme de Baire assurerait alors que 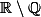 ou
ou  ne serait pas d'intérieur vide ce qui n'est pas.
ne serait pas d'intérieur vide ce qui n'est pas.
Modifié en dernier par Tuvasbien le 16 Aoû 2019, 21:09, modifié 1 fois.
Re: fonction continue sur les rationnels
Notons aussi que le contre-exemple 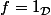 avec
avec ) n'en est pas un, le fait que
n'en est pas un, le fait que  soit constante sur
soit constante sur  ne montre pas qu'elle y est continue pour autant, le contre-exemple mentionné plus haut :
ne montre pas qu'elle y est continue pour autant, le contre-exemple mentionné plus haut : 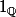 en est la preuve même,
en est la preuve même, 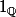 est constante sur
est constante sur  mais est continue nulle part ! Conclusion la fonction
mais est continue nulle part ! Conclusion la fonction 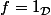 n'est continue nulle part et n'est pas un contre exemple, on peut le montrer de la même façon que pour
n'est continue nulle part et n'est pas un contre exemple, on peut le montrer de la même façon que pour 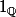 en utilisant la densité de
en utilisant la densité de 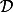 dans
dans 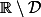 .
.
Re: fonction continue sur les rationnels
Ça me rappelle le fameux (?) "une fonction est toujours constante en un point donc sa dérivée y est forcément nulle".
Sinon, plus sérieusement, je trouve un peu dommage de réagir ici aux messages trollesques/ad hominem postés ailleurs. Autant j'admire le soin dont GaBuZoMeu arrive à faire preuve dans ses réponses à toutes les attaques contre lui, autant je ne suis pas bien sûr que l'effet global soit positif. J'ai l'impression qu'au final ça donne de l'attention à des choses qui ne le méritent pas, et que ça ramène ici des toxines dont il n'a déjà pas été très aisé de se débarrasser...
Enfin ce n'est que mon avis. Bon courage cela dit !
Sinon, plus sérieusement, je trouve un peu dommage de réagir ici aux messages trollesques/ad hominem postés ailleurs. Autant j'admire le soin dont GaBuZoMeu arrive à faire preuve dans ses réponses à toutes les attaques contre lui, autant je ne suis pas bien sûr que l'effet global soit positif. J'ai l'impression qu'au final ça donne de l'attention à des choses qui ne le méritent pas, et que ça ramène ici des toxines dont il n'a déjà pas été très aisé de se débarrasser...
Enfin ce n'est que mon avis. Bon courage cela dit !
Re: fonction continue sur les rationnels
Je suis d'accord avec toi Skullkid.
GaBuZoMeu tu sembles avoir un très bon niveau sur le forum et tu es toujours disponible pour aider tout le monde, pourquoi as-tu sans cesse besoin de revenir sur les propos d'autres individus bannis de ce forum qui semblent toujours avoir quelque chose à dire sur tes propos ? Je te conseille de ne même plus lire et de focus sur l'aide, déjà très remarquable, que tu apportes sur le forum (:
GaBuZoMeu tu sembles avoir un très bon niveau sur le forum et tu es toujours disponible pour aider tout le monde, pourquoi as-tu sans cesse besoin de revenir sur les propos d'autres individus bannis de ce forum qui semblent toujours avoir quelque chose à dire sur tes propos ? Je te conseille de ne même plus lire et de focus sur l'aide, déjà très remarquable, que tu apportes sur le forum (:
Re: fonction continue sur les rationnels
Bonjour,
Si un petit clown lançait un fil "les bourdes de Skullkid/Yezu" en faisant la preuve qu'il lit de travers ce que vous avez écrit et qu'il ne comprend pas les arguments donnés, refuseriez-vous de vous payer sa tête ?
Si les zozos du forum Dlz9 m'en veulent à ce point, c'est parce que ça fait longtemps que je dégonfle leurs baudruches, sur les forums qu'ils fréquentaient avant de se faire exclure. On peut faire une différence entre les deux, les interventions de Dattier avaient quelquefois un contenu mathématique pas inintéressant, mais qui demandait à être retravaillé. Mais ces derniers temps, ça s'est nettement gâté.
Maintenant, j'accorde peut-être trop d'attention au forum de Dlzlogic. Son contenu fait qu'il n'en mérite aucune, je suis d'accord. N'en parlons plus.
Si un petit clown lançait un fil "les bourdes de Skullkid/Yezu" en faisant la preuve qu'il lit de travers ce que vous avez écrit et qu'il ne comprend pas les arguments donnés, refuseriez-vous de vous payer sa tête ?
Si les zozos du forum Dlz9 m'en veulent à ce point, c'est parce que ça fait longtemps que je dégonfle leurs baudruches, sur les forums qu'ils fréquentaient avant de se faire exclure. On peut faire une différence entre les deux, les interventions de Dattier avaient quelquefois un contenu mathématique pas inintéressant, mais qui demandait à être retravaillé. Mais ces derniers temps, ça s'est nettement gâté.
Maintenant, j'accorde peut-être trop d'attention au forum de Dlzlogic. Son contenu fait qu'il n'en mérite aucune, je suis d'accord. N'en parlons plus.
Re: fonction continue sur les rationnels
Skullkid a écrit:, et que ça ramène ici des toxines dont il n'a déjà pas été très aisé de se débarrasser...
Pas du tout aisé je confirme !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
