Image inverse des rationnels

par **Imod** » 06 Juil 2009, 07:48

Bonjour :we:

Soit

un polynôme à coefficients rationnels .

Il est clair que

. Quelle condition faut-il imposer à

pour que

?

Bon courage :zen:

Imod

par **yos** » 08 Juil 2009, 17:53

degré de P < 2

par **Imod** » 08 Juil 2009, 18:10

Il y a de l'idée mais il me semble qu'il y a un problème avec l'image réciproque d'un polynôme constant à valeur rationnelle :zen:

Imod

par **Imod** » 17 Juil 2009, 22:31

Peu de réponse à part l'intervention minimaliste de yos :cry:

Je propose le lemme suivant :

Pour tout polynôme

unitaire à coefficients dans

et de degré supérieur à 1 , il existe un irrationnel

tel que

.

Bon courage :we:

Imod

par **leon1789** » 18 Juil 2009, 14:08

Imod a écrit:Pour tout polynôme unitaire à coefficients dans et de degré supérieur à 1 , il existe un irrationnel tel que .

Ok, pas trop difficile avec un coup de TVI (...et aussi Z intégralement clos).

par **Imod** » 18 Juil 2009, 23:46

leon1789 a écrit:Ok, pas trop difficile avec un coup de TVI

D'accord :++:

leon1789 a écrit:...et aussi Z intégralement clos

Oupss... mes souvenirs d'algèbre datent un peu mais Z intégralement clos je n'y crois pas trop :triste:

PS : après vérification , c'est bon , je confondais avec algébriquement clos :briques:

Imod

par **ffpower** » 19 Juil 2009, 00:00

Doit falloir plutot utiliser que l ensemble des rationnels envoyés sur un entier ont un dénominateur majoré(par le coeff dominant)

par **skilveg** » 19 Juil 2009, 07:29

Allez, je me lance.

Preuve du lemme: on prend

de degré >1, unitaire et à coefficients dans

. Pour

assez grand, on a

; par ailleurs, il existe des valeurs arbitrairement grandes s'envoyant sur un entier; prenons-en une, disons

. Alors

, et par les valeurs intermédiaires il existe

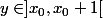
tel que

. Mais comme

n'est pas entier, par un résultat classique (équivalent au fait que

est intégralement clos),

est irrationnel.

Preuve du résultat: "si

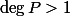
avec

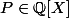
, alors il existe

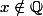
tel que

. En particulier, si

, alors

."

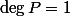
On note

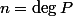
et on prend

un ppcm des dénominateurs des coefficients de

; alors

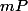
est à coefficients entiers et a un coefficient dominant entier

. On pose

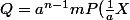, qui est encore à coefficients entiers, unitaire et de degré

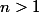
. Par le lemme, il existe

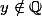
tel que

, donc

, cqfd.

par **Imod** » 19 Juil 2009, 10:00

Oui skilveg , il n'y a plus qu'à conclure :zen:

Imod

Image inverse des rationnels

Image inverse des rationnels

Qui est en ligne