Facile et simple ne sont pas confondus
Facile et simple ne sont pas confondus
Bonjour,
Le but de ce fil est de montrer que ce n'est pas parce que c'est simple (compréhensible du plus grand nombre) que c'est facile à trouver.
Ici des exemples de tels énoncés pour savoir de quoi il retourne :
http://www.les-mathematiques.net/phorum ... 43,1198849
Donc pour cela je vais proposer des énoncés dont la solution fait moins d'une dizaine de ligne, en me basant sur le programme de l'agreg (maximum).
Pour la solution proposée par, me semble-t-il, Guy Casale :
Les détails sont ici, je précise que je ne savais pas que cette formule avait un nom particulier :
https://fr.wikipedia.org/wiki/Formule_de_Legendre
Bonne journée.
Le but de ce fil est de montrer que ce n'est pas parce que c'est simple (compréhensible du plus grand nombre) que c'est facile à trouver.
Ici des exemples de tels énoncés pour savoir de quoi il retourne :
http://www.les-mathematiques.net/phorum ... 43,1198849
Donc pour cela je vais proposer des énoncés dont la solution fait moins d'une dizaine de ligne, en me basant sur le programme de l'agreg (maximum).
Pour la solution proposée par, me semble-t-il, Guy Casale :
Les détails sont ici, je précise que je ne savais pas que cette formule avait un nom particulier :
https://fr.wikipedia.org/wiki/Formule_de_Legendre
Bonne journée.
Re: Facile et simple ne sont pas confondus
Salut,
Ca commence mal, rien que l'énoncé 1 du lien, je comprend que dalle :
Pour tout j de {1..n}, vu que r(E)=E, on a r(Aj)=Ak pour un certain k.
Sauf que d(Ai,O)=i pour tout i de {1..n} (*) et en particulier k=d(Ak,O)=d(r(Aj),r(O))=d(Aj,O)=j vu que r est une isométrie.
Donc r(Aj)=Aj et comme le seul point fixe de r est O, c'est que Aj=O (pour tout j) ce qui est clairement contradictoire avec le d(O,Aj)=j...
(*) Là, le "pour tout i de {1..n}", je l'invente vu qu'il n'y a rien de précisé dans l'énoncé, mais je vois pas comment rendre l'énoncé cohérent autrement qu'en sous entendant ce "pour tout i".
Pour l'énoncé 2, est-ce que C([0,1]) c'est l'ensemble des applications continues de [0,1] dans [0,1] muni de la distance\!=\!\mathop{\max}\limits_{x\in[0,1]}|f(x)\!-\!g(x)|) ? (Usuellement, pour un compact K, C(K), ça désigne l'espace de Banach des fonctions continues de K dans R (ou C) muni de la norme sup, mais là, ça peut clairement pas être ça vu que c'est pas contenu dans F([0,1])))
? (Usuellement, pour un compact K, C(K), ça désigne l'espace de Banach des fonctions continues de K dans R (ou C) muni de la norme sup, mais là, ça peut clairement pas être ça vu que c'est pas contenu dans F([0,1])))
Si c'est bien ça C alors le résultat est NON pour une simple raison de cardinalité.
Ca commence mal, rien que l'énoncé 1 du lien, je comprend que dalle :
Pour tout j de {1..n}, vu que r(E)=E, on a r(Aj)=Ak pour un certain k.
Sauf que d(Ai,O)=i pour tout i de {1..n} (*) et en particulier k=d(Ak,O)=d(r(Aj),r(O))=d(Aj,O)=j vu que r est une isométrie.
Donc r(Aj)=Aj et comme le seul point fixe de r est O, c'est que Aj=O (pour tout j) ce qui est clairement contradictoire avec le d(O,Aj)=j...
(*) Là, le "pour tout i de {1..n}", je l'invente vu qu'il n'y a rien de précisé dans l'énoncé, mais je vois pas comment rendre l'énoncé cohérent autrement qu'en sous entendant ce "pour tout i".
Pour l'énoncé 2, est-ce que C([0,1]) c'est l'ensemble des applications continues de [0,1] dans [0,1] muni de la distance
Si c'est bien ça C alors le résultat est NON pour une simple raison de cardinalité.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Facile et simple ne sont pas confondus
Arbre a écrit:Le but de ce fil est de montrer que ce n'est pas parce que c'est simple (compréhensible du plus grand nombre) que c'est facile à trouver.
Ici des exemples de tels énoncés pour savoir de quoi il retourne :
http://www.les-mathematiques.net/phorum ... 43,1198849
Bonjour Un_homme,
Et faut-il venir sur un forum pour mettre le lien d'une discussion d'un autre forum?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Facile et simple ne sont pas confondus
Salut,
@Ben : effectivement l'énoncé 1 est bugguer.
L'énoncé 2 :) est l'ensemble des fonctions continues de [0,1] dans lui même,
est l'ensemble des fonctions continues de [0,1] dans lui même, ) l'ensemble des fonctions de [0,1] dans lui même.
l'ensemble des fonctions de [0,1] dans lui même.
Bravo, c'est bien un argument de cardinal, qui permet de conclure.
@Lostounet : oui, je vais reproduire ici les énoncés qui me semble le plus intéressant, en guise d'entrainement...
Entrainement 1 :
On pose=x^2+1) dans
dans 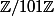 . Calculer la dérivée 101e de
. Calculer la dérivée 101e de 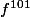 en 2.
en 2.
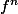 est la composée de
est la composée de  n fois.
n fois.
Entrainement 2 :
On pose=x^2+1) dans
dans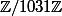 . Calculer la dérivée 101 e de
. Calculer la dérivée 101 e de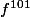 en 2.
en 2.
Entrainement 3 :
Soit fonction de
fonction de  dans lui même, de norme
dans lui même, de norme 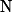 , continue tel que :
, continue tel que :
pour tout de
de  on suppose :
on suppose :  \leq \text{N}(f(x)-f(y)))
Prouver que a un point fixe.
a un point fixe.
Entrainement 4 :
Existe-t-il de [0,1] dans lui même tel que :
de [0,1] dans lui même tel que :
+f(1-x)+x=3f(x)) pour tout
pour tout  dans [0,1] ?
dans [0,1] ?
Entrainement 5 :
Calculer à la main, pour tout ,
, ) .
.
On rappelle que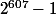 est premier.
est premier.
Entrainement 6 :
Calculer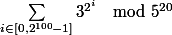 .
.
Entrainement 7 + :
Montrer que pour tout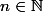 , si
, si =n^2+1) alors
alors 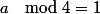 .
.
Entrainement 8 :
Soit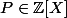 de degré
de degré  tel qu'il existe
tel qu'il existe 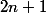 valeurs entières pour lesquelles
valeurs entières pour lesquelles  vaut un nombre premier, peut-on dire qu'alors
vaut un nombre premier, peut-on dire qu'alors  est irréductible sur
est irréductible sur  ?
?
Entrainement 9 :
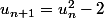 trouver l'expression générale de
trouver l'expression générale de  en fonction de
en fonction de  ?
?
Entrainement 10 ++ :
 fonction continue de
fonction continue de  dans
dans=\R) . Montrer que pour tout
. Montrer que pour tout 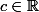 ,
, =c\}) est de cardinal
est de cardinal  .
.
Entrainement 11 :
Soit un polynôme de
un polynôme de 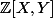 tel que
tel que =P(2,4)=P(4,4)=P(1,2)=c) et
et =3+c) .
.
Montrer que pour tout\neq R(X)+Q(Y))
Entrainement 12 :
On note_2) la factorielle de
la factorielle de  alléger de 2, qui est le produit des nombres entre
alléger de 2, qui est le produit des nombres entre  et
et  , à l'exception des nombres pairs.
, à l'exception des nombres pairs.
Calculer :_2\mod 2^{101})
A suivre...
Bonne soirée.
@Ben : effectivement l'énoncé 1 est bugguer.
L'énoncé 2 :
Bravo, c'est bien un argument de cardinal, qui permet de conclure.
@Lostounet : oui, je vais reproduire ici les énoncés qui me semble le plus intéressant, en guise d'entrainement...
Entrainement 1 :
On pose
Entrainement 2 :
On pose
Entrainement 3 :
Soit
pour tout
Prouver que
Entrainement 4 :
Existe-t-il
Entrainement 5 :
Calculer à la main, pour tout
On rappelle que
Entrainement 6 :
Calculer
Entrainement 7 + :
Montrer que pour tout
Entrainement 8 :
Soit
Entrainement 9 :
Entrainement 10 ++ :
Entrainement 11 :
Soit
Montrer que pour tout
Entrainement 12 :
On note
Calculer :
A suivre...
Bonne soirée.
Re: Facile et simple ne sont pas confondus
Entrainement 13 + :
B l'ensemble des fonctions de [0,1] dans [0,1], muni de la métrique=\sup\limits_{x\in[0,1]} |f(x)-g(x)|) .
.
Le sous-ensemble des fonctions continues en 0, y-est-il dense ?
Entrainement 14 :
Soit une fonction
une fonction  de
de  dans lui même tel que
dans lui même tel que \neq 0) , montrer qu'alors
, montrer qu'alors  admet une valeur propre entière (càd il existe
admet une valeur propre entière (càd il existe  entier et
entier et 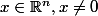 tel que
tel que =k.x)) .
.
Entrainement 15 :
Calculer^2-1} \mod(2^{607}-1))
Entrainement 16 :
Déterminer le terme générale de la suite) avec
avec 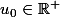 et
et 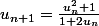
Entrainement 17 :
Soit continue de
continue de  dans lui même, avec
dans lui même, avec  compact connexe de
compact connexe de  . A-t-on alors
. A-t-on alors  admet un point fixe ?
admet un point fixe ?
Entrainement 18 + :
On note_p) est la factorielle allégée de
est la factorielle allégée de  , c'est le plus grand entier, premier avec
, c'est le plus grand entier, premier avec  et qui divise
et qui divise 
Montrer que pour tout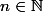 tel que
tel que 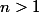 et
et  entier premier :
entier premier :
_p|(p-1)...(p^n-1))
Entrainement 19 :
Soient un entier premier impair,
un entier premier impair, [x]) tel que
tel que <p) et
et =a_0+...+a_{p-1}x^{p-1})
Montrer que si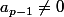 alors la fonction polynôme associé à
alors la fonction polynôme associé à  n'est pas une permutation de
n'est pas une permutation de 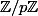 .
.
Entrainement 20 :
La série suivante converge-t-elle :
})}{\ln(2)}+\frac{\sin(2+\frac{1}{\ln(3)})}{\ln(3)}+...+\frac{\sin(n+\frac{1}{\ln(n+1)})}{\ln(n+1)})
Entrainement 21 +++ :
Soit nombre entier plus grand que 5,
nombre entier plus grand que 5,  un sous-groupe de
un sous-groupe de 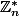 .
.
Montrer que si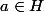 avec
avec 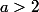 alors
alors |\sum \limits_{h \in H} n(-\frac{h}{n} \mod a)) .
.
Entrainement 22 :
A-t-on
\in (\N,>0)^k} \frac{1}{(n_1+...+n_k)^a}<+\infty \text{ ssi } a>k)
?
Entrainement 23 + :
On note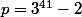 , on prend
, on prend _n) la suite récurrente de
la suite récurrente de 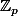 tel que
tel que 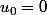 et
et 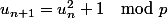 .
.
Existe-t-il un rang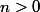 tel que
tel que  ?
?
Entrainement 24 :
Soit un nombre premier et
un nombre premier et  un élément primitif du groupe multiplicatif de
un élément primitif du groupe multiplicatif de 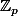 .
.
Montrer que (on notera la fonction partie entière ) :
la fonction partie entière ) :
+...+E(\frac{b^{p-1}}{p})=\frac{b^p-b}{p(b-1)}-\frac{(p-1)}{2})
B l'ensemble des fonctions de [0,1] dans [0,1], muni de la métrique
Le sous-ensemble des fonctions continues en 0, y-est-il dense ?
Entrainement 14 :
Soit
Entrainement 15 :
Calculer
Entrainement 16 :
Déterminer le terme générale de la suite
Entrainement 17 :
Soit
Entrainement 18 + :
On note
Montrer que pour tout
Entrainement 19 :
Soient
Montrer que si
Entrainement 20 :
La série suivante converge-t-elle :
Entrainement 21 +++ :
Soit
Montrer que si
Entrainement 22 :
A-t-on
?
Entrainement 23 + :
On note
Existe-t-il un rang
Entrainement 24 :
Soit
Montrer que (on notera
Re: Facile et simple ne sont pas confondus
Salut,
énoncé 1 : critère nécessaire de groupitude ?
a/ Soit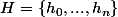 un sous-groupe multiplicatif de
un sous-groupe multiplicatif de 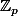 (
( premier), avec
premier), avec 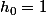 et les
et les 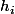 distincts, différent de
distincts, différent de  .
.
A-t-on\times...\times(h_n-1)\mod p=o(H)) ?
?
b/ On suppose que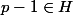 .
.
A-t-on\times...\times(h_n-1)\mod p=p-o(H)) ?
?
énoncé 2 : plein les sinus
Calculer, modulo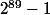 , la dérivée 100-iem en 0 de
, la dérivée 100-iem en 0 de 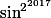 (fonction composée de
(fonction composée de 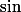 ) ?
) ?
inutile de faire le calcul :
Comment calculer, en moins de 10 minutes avec un pc récent, la dérivée 100-iem en 0 de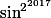 (fonction composée de
(fonction composée de 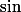 ) ?
) ?
Bonne journée.
énoncé 1 : critère nécessaire de groupitude ?
a/ Soit
A-t-on
b/ On suppose que
A-t-on
énoncé 2 : plein les sinus
Calculer, modulo
inutile de faire le calcul :
Comment calculer, en moins de 10 minutes avec un pc récent, la dérivée 100-iem en 0 de
Bonne journée.
Modifié en dernier par Arbre le 05 Jan 2017, 12:19, modifié 2 fois.
Re: Facile et simple ne sont pas confondus
Je comprend rien à tes notations :
Déjà, le "mod p", placé où il est, il ne veut rien dire : la syntaxe normale étant "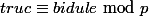 " : "truc est congru à bidule modulo p" avec un congru et pas un égal.
" : "truc est congru à bidule modulo p" avec un congru et pas un égal.
Ensuite, le o(H), tout ce que ça évoque pour moi, c'est les notation de Landeau pour des Comparaison_asymptotique et je vois vraiment pas ce que ça viendrait f.. ici.
Sinon, si H est un sous groupe multiplicatif de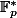 , il est forcément cyclique et on a
, il est forcément cyclique et on a  divise
divise 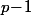 .
.
Et réciproquement, pour tout qui divise
qui divise 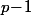 , il existe un unique sous groupe multiplicatif de
, il existe un unique sous groupe multiplicatif de 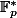 qui soit de cardinal
qui soit de cardinal  et ces éléments sont exactement les solutions de
et ces éléments sont exactement les solutions de 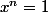 (donc
(donc 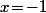 est dans H ssi
est dans H ssi  est pair)
est pair)
Il en résulte que) donc que
donc que \!:=\!\!\!\prod_{h\in H\backslash\{1\}}\!\!\!\!(X\!-\!h)=\dfrac{X^n\!-\!1}{X\!-\!1}=1\!+\!X\!+\!X^2...+\!X ^{n-1}) .
.
On a donc=(-1)^{n-1}P(1)=(-1)^{n-1}n)
Le truc en rouge, il est sensé vouloir dire quoi ?Arbre a écrit:
Déjà, le "mod p", placé où il est, il ne veut rien dire : la syntaxe normale étant "
Ensuite, le o(H), tout ce que ça évoque pour moi, c'est les notation de Landeau pour des Comparaison_asymptotique et je vois vraiment pas ce que ça viendrait f.. ici.
Sinon, si H est un sous groupe multiplicatif de
Et réciproquement, pour tout
Il en résulte que
On a donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Facile et simple ne sont pas confondus
Ici o(H) c'est l'ordre du groupe H, c'est une notation, que je crois, standard que j'ai vu lors de mes études, ensuite 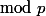 il a bien le sens de la congruence (c'est le reste par la division euclidienne).
il a bien le sens de la congruence (c'est le reste par la division euclidienne).
Bravo.
Bonne journée.
Bravo.
Bonne journée.
Modifié en dernier par Arbre le 05 Jan 2017, 12:34, modifié 2 fois.
Re: Facile et simple ne sont pas confondus
énoncé 3 : équations fonctionnelles
Soient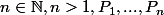 polynômes complexes.
polynômes complexes.
Si=a_0+...+a_nX^n) ,
,  une fonction de
une fonction de 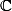 dans
dans 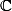 , on note
, on note ) la fonction :
la fonction : =a_0id+a_1f+...+a_nf^n) avec
avec =f(f(x))) .
.
Trouver une condition nécessaire et suffisante (sur les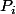 ) pour qu'il existe une fonction
) pour qu'il existe une fonction  de
de 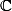 dans
dans 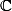 tel que :
tel que : =0)
énoncé 4 : Diffie-Helmann par les polynômes
Soit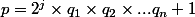 un nombre premier, avec les
un nombre premier, avec les 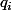 premiers entre eux et impairs soit
premiers entre eux et impairs soit  un polynôme de deux variable dans
un polynôme de deux variable dans 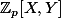 avec
avec  un générateur de
un générateur de 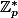 , tel que pour tout
, tel que pour tout \mod p) .
.
Alors) .
.
Bonne journée.
Soient
Si
Trouver une condition nécessaire et suffisante (sur les
énoncé 4 : Diffie-Helmann par les polynômes
Soit
Alors
Bonne journée.
Modifié en dernier par Arbre le 05 Jan 2017, 19:27, modifié 2 fois.
Re: Facile et simple ne sont pas confondus
Je ne donnerais la solution que si l'ensemble des participants à ce fil, reconnaisse que ce n'est pas parce qu'une solution est simple (compréhensible du plus grand nombre) qu'elle est facile à trouver.
Je considérerais avoir perdu mon défi, si au moins 3 énoncés sur 4 sont résolus (déjà 1 de tomber).
A bientôt.
Je considérerais avoir perdu mon défi, si au moins 3 énoncés sur 4 sont résolus (déjà 1 de tomber).
A bientôt.
Re: Facile et simple ne sont pas confondus
Arbre a écrit:Je ne donnerais la solution que si l'ensemble des participants à ce fil, reconnaisse que ce n'est pas parce qu'une solution est simple (compréhensible du plus grand nombre) qu'elle est facile à trouver.
Je considérerais avoir perdu mon défi, si au moins 3 énoncés sur 4 sont résolus (déjà 1 de tomber).
A bientôt.
cela n' a pas de sens, la résolution par Ben314 ou par moi -même n' a pas la même valeur de démonstration.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Facile et simple ne sont pas confondus
"reconnaisse que ce n'est pas parce qu'une solution est simple (compréhensible du plus grand nombre) qu'elle est facile à trouver."
mais ceci est une évidence, donc je le reconnais
en voilà 1.
mais ceci est une évidence, donc je le reconnais
en voilà 1.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Facile et simple ne sont pas confondus
Exactement la même chose pour moi et je suis persuadé qu'absolument toutes les personnes qui ont fait un tant soit peu de math dans leur vie en sont tout aussi convaincus.beagle a écrit:"reconnaisse que ce n'est pas parce qu'une solution est simple (compréhensible du plus grand nombre) qu'elle est facile à trouver."
mais ceci est une évidence, donc je le reconnais
en voilà 1.
De plus, perso., si je devait trouver des exemples de "trucs simples dont le preuve est difficile à trouver", ben j'irais surement pas chercher dans des domaines aussi complexes que les congruence ou les groupes finis, mais bien plus simplement en géométrie où on trouve très facilement des problèmes dont la preuve est extrêmement difficile à trouver alors qu'elle est très courte est tout à fait compréhensible pour un collégien (par exemple le fameux problème de Langley).
Enfin, bref, je trouve ça très bien (*) de mettre des énigmes/défis quelque soit le niveau (surtout vu qu'en ce moment on peut pas dire qu'il y ait foule), mais le coté "je vais vous prouver qu'il y a des trucs simple et court mais difficile à trouver", je trouve ça passablement con vu que tout le monde le sait depuis longtemps.
(*) Encore que 24+4 problèmes dans un même thread et en moins de 48h, je sais pas si c'est bien futé comme technique : si on se met à répondre à tous en même temps, je te dit pas la lisibilité du thread...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Facile et simple ne sont pas confondus
SoientArbre a écrit:énoncé 3 : équations fonctionnelles
Soientpolynômes complexes.
Si,
une fonction de
dans
, on note
la fonction :
avec
.
Trouver une condition nécessaire et suffisante (sur les) pour qu'il existe une fonction
de
dans
tel que :
[/tex]
- Si
- Si
Et on en déduit via l'algo. d'Euclide que, si
C'est évidement impossible si le
Et si ça n'est pas le cas, alors les
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Facile et simple ne sont pas confondus
Et là, je comprend toujours que dalle :Arbre a écrit:[énoncé 4 : Diffie-Helmann par les polynômes
Soitun nombre premier, avec les
premiers entre eux et impairs soit
un polynôme de deux variable dans
avec
un de ses éléments primitifs tel que pour tout
.
Alors.
- Les mod sont toujours autant placés en dépit du bon sens (parle à mon cul; ma tête est malade...) (*)
- C'est quoi un "élément primitif" d'un polynôme ?
(*) Si tu tient à parler de "reste de division par p" plutôt que de congruence, ben le mini du mini, ça serait d'utiliser un symbole qui ne désigne pas déjà autre chose en mathématique. Les (très rares) fois où j'ai vu utiliser un symbole pour le reste de la division euclidienne, c'est le symbole % que j'ai vu.
P.S. Et si ça t'intéresse, l'ordre d'un groupe H, c'est noté quasi unanimement |H|, parfois #H (le # servant souvent comme raccourci pour "cardinal") et très très rarement ord(H). Mais jamais o(H).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Facile et simple ne sont pas confondus
@Ben pour le 3 : bravo.
Bien évidement, moi aussi j'en suis convaincu.
Est-ce que Lostounet, l'est également ?
Bonne journée.
Bien évidement, moi aussi j'en suis convaincu.
Est-ce que Lostounet, l'est également ?
Bonne journée.
Re: Facile et simple ne sont pas confondus
Le défi a été relevé : http://www.les-mathematiques.net/phorum ... 43,1386282
Bravo à tous les participants, avec une mention spéciale pour Ben.
Bonne soirée.
Bravo à tous les participants, avec une mention spéciale pour Ben.
Bonne soirée.
Re: Facile et simple ne sont pas confondus
Je vous laisse le 4 à chercher, sauf si on me demande la réponse et alors comme promis je donne ma réponse.
Bonne soirée.
Bonne soirée.
Re: Facile et simple ne sont pas confondus
Bonjour,
On commence doucement avec entrainement 1 :
On pose=x^2+1) dans
dans 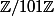 . Calculer la dérivée 101e de
. Calculer la dérivée 101e de 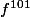 en 2.
en 2.
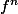 est la composée de
est la composée de  n fois.
n fois.
Bonne journée.
On commence doucement avec entrainement 1 :
On pose
Bonne journée.
Re: Facile et simple ne sont pas confondus
Ben celui là,
a) Il est archi. mal formulé, en particulier avec son dans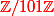 qui laisse franchement à penser que
qui laisse franchement à penser que  et
et ) sont des éléments de
sont des éléments de 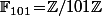 alors que si effectivement c'était le cas, c'est à dire si f était définie comme une fonction de
alors que si effectivement c'était le cas, c'est à dire si f était définie comme une fonction de 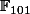 dans lui même, on ne risquerais pas de dériver quoi que ce soit vu que la notion de dérivée n'a aucun sens sur l'ensemble des fonctions de
dans lui même, on ne risquerais pas de dériver quoi que ce soit vu que la notion de dérivée n'a aucun sens sur l'ensemble des fonctions de 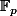 dans lui même.
dans lui même.
Bref, il faut ABSOLUMENT écrire\!=\!X^2\!+\!1\in{\mathbb F}_ {101}[X]) c'est à dire définir
c'est à dire définir  comme un polynôme formel (*) si tu veut que la notion de dérivation ait du sens.
comme un polynôme formel (*) si tu veut que la notion de dérivation ait du sens.
b) Une fois que l'on se place dans le cas des polynôme formel, l'exo n'a aucun intérêt vu que dans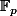 , l'endomorphisme "dérivée
, l'endomorphisme "dérivée  -ième" est l'endomorphisme nul (si on dérive
-ième" est l'endomorphisme nul (si on dérive  fois
fois 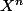 , on obtient
, on obtient ...(n\!-\!(p\!-\!1))X^{n-p}) et il y a forcément un multiple de
et il y a forcément un multiple de  dans le produit précédent le
dans le produit précédent le 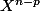 ).
).
(*) Et vu que les notions de polynômes formels et de fonctions polynômes ne coïncide pas sur les corps fini, la distinction entre les deux n'est pas du tout "un détail", mais quelque chose d'extrêmement important.
a) Il est archi. mal formulé, en particulier avec son dans
Bref, il faut ABSOLUMENT écrire
b) Une fois que l'on se place dans le cas des polynôme formel, l'exo n'a aucun intérêt vu que dans
(*) Et vu que les notions de polynômes formels et de fonctions polynômes ne coïncide pas sur les corps fini, la distinction entre les deux n'est pas du tout "un détail", mais quelque chose d'extrêmement important.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
