J'ai vu ça quelque part: Démontrer que si n est impair
Expression à justifier
12 messages
- Page 1 sur 1
Re: Expression à justifier
Salut,
=\Big((X\!+\!1)^2-2X\!\Big)^{\!\!n}\!<br />=\sum_{i=0}^n{n\choose i}\big(X\!+\!1\big)^{2i}\big(\!-\!2X\big)^{n-i}<br />=\sum_{i=0}^n{n\choose i}\big(\!-\!2X\big)^{n-i}\sum_{j=0}^{2i}{2i\choose j}X^j)
^{n-i}X^{n-i+j}<br />=\sum_{k=0}^{2n}c_k X^k)
avec^{n-i})
Mais d'un autre coté, on a aussi=\big(X^2\!+\!1\big)^{n}\!<br />=\sum_{\ell=0}^n{n\choose \ell}X^{2\ell})
Donc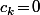 pour
pour  impair et
impair et 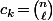 si
si 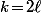 .
.
(L'égalité demandé correspondant au cas particulier k=n impair)
avec
Mais d'un autre coté, on a aussi
Donc
(L'égalité demandé correspondant au cas particulier k=n impair)
Modifié en dernier par Ben314 le 13 Oct 2017, 20:07, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Expression à justifier
Bonjour
@ben Oui c'est intéressant comme solution surtout parce qu'elle utilise des moyens élémentaires.
Je donne donc la mienne^i) est une série hypergéométrique
est une série hypergéométrique
plus précisément cela vaut F(-n,1/2,1,2). c'est facile à vérifier
Maintenant on sait que=\Gamma( b)\Gamma(c-b)/\Gamma( c)\int_0^1 u^{b-1}(1-u)^{c-b-1}(1-uz)^{-a} du)
Il s'agit maintenant de calculer cette dernière intégrale qui dans notre cas est:
^{-1/2}(1-2u)^n du)
Elle vaut évidemment 0 quand n est impair à cause de la symétrie par rapport à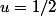 . cqfd
. cqfd
@ben Oui c'est intéressant comme solution surtout parce qu'elle utilise des moyens élémentaires.
Je donne donc la mienne
plus précisément cela vaut F(-n,1/2,1,2). c'est facile à vérifier
Maintenant on sait que
Il s'agit maintenant de calculer cette dernière intégrale qui dans notre cas est:
Elle vaut évidemment 0 quand n est impair à cause de la symétrie par rapport à
Re: Expression à justifier
Ben314 a écrit:Salut,^{n-i}X^{n-i+j}<br />=\sum_{k=0}^{2n}c_k X^k)
avec^{n-i})
Mais d'un autre coté, on a aussi
Doncpour
impair et
si
.
(L'égalité demandé correspondant au cas particulier k=n impair)
Salut,
Au risque de paraitre débile mais comment vois-tu en amont que faut-il développer en somme double pour retomber sur ses pieds à la fin?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Expression à justifier
Ca, c'est "quasi mécanique" :
1) Quand tu as des trucs avec des sommes et des tas de factorielles, faut forcément les écrire en terme de coeffs. binomiaux pour arriver à en tirer quelque chose.
Et là, ben c'est pas la peine d'être bien futé pour voir que c'est les coeff (2i ; i) et (n ; i) qui sont "camouflés" dans la formule.
2) Ensuite, le coeff (n ; i), il apparait naturellement dans n'importe quel développement (A+B)^n avec derrière du A^(n-i) et du B^i
Et le coef (2i ; i) il apparait naturellement dans (C+D)^(2i) [comme un coeff. particulier et ça, ça signifie que la formule demandé est sans doute un cas particulier d'une formule plus générale]
Avec ça, ben tu as la réponse : pour faire apparaitre on ne peut plus naturellement le produit (n ; i) par (2i ; i), ben il suffit de développer [A+(C+D)^2]^n. Donc tu développe tel le bourrin avec des A, des C et des D.
Ensuite, tu as en fait des tonnes de produits (2i ; j) [et pas (2i ; i)] par (n ; i) et tu regarde comment te demerder avec les puissance qu'il y a sur les A,C et D pour que ça regroupe "naturellement" les produits (2i ; j) par (n ; i) dans lesquels on a j=i.
Et là, il y a des tonnes de solution : la première que j'avais proposée, c'était avec A=-2 ; C=X et D=1/X et puis j'ai trouvé plus joli avec A=-2X ; B=X et C=1
Enfin, bref, c'est pas du tout un truc qui demande "des tonnes d'imagination", mais plutôt un truc "parfaitement balisé".
EDIT : J'ai oulié un truc : la formule de départ, elle contient aussi du (-1/2)^i donc avec tes A, B et C, ben faut que tu te démerde pour qu'il y ait simplification lorsque j=i et aussi qu'il y ait du (-1/2)^i qui apparaisse.
1) Quand tu as des trucs avec des sommes et des tas de factorielles, faut forcément les écrire en terme de coeffs. binomiaux pour arriver à en tirer quelque chose.
Et là, ben c'est pas la peine d'être bien futé pour voir que c'est les coeff (2i ; i) et (n ; i) qui sont "camouflés" dans la formule.
2) Ensuite, le coeff (n ; i), il apparait naturellement dans n'importe quel développement (A+B)^n avec derrière du A^(n-i) et du B^i
Et le coef (2i ; i) il apparait naturellement dans (C+D)^(2i) [comme un coeff. particulier et ça, ça signifie que la formule demandé est sans doute un cas particulier d'une formule plus générale]
Avec ça, ben tu as la réponse : pour faire apparaitre on ne peut plus naturellement le produit (n ; i) par (2i ; i), ben il suffit de développer [A+(C+D)^2]^n. Donc tu développe tel le bourrin avec des A, des C et des D.
Ensuite, tu as en fait des tonnes de produits (2i ; j) [et pas (2i ; i)] par (n ; i) et tu regarde comment te demerder avec les puissance qu'il y a sur les A,C et D pour que ça regroupe "naturellement" les produits (2i ; j) par (n ; i) dans lesquels on a j=i.
Et là, il y a des tonnes de solution : la première que j'avais proposée, c'était avec A=-2 ; C=X et D=1/X et puis j'ai trouvé plus joli avec A=-2X ; B=X et C=1
Enfin, bref, c'est pas du tout un truc qui demande "des tonnes d'imagination", mais plutôt un truc "parfaitement balisé".
EDIT : J'ai oulié un truc : la formule de départ, elle contient aussi du (-1/2)^i donc avec tes A, B et C, ben faut que tu te démerde pour qu'il y ait simplification lorsque j=i et aussi qu'il y ait du (-1/2)^i qui apparaisse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Expression à justifier
aviateur a écrit:Bonjour
@ben Oui c'est intéressant comme solution surtout parce qu'elle utilise des moyens élémentaires.
Je donne donc la mienneest une série hypergéométrique
plus précisément cela vaut F(-n,1/2,1,2). c'est facile à vérifier
Maintenant on sait que
Il s'agit maintenant de calculer cette dernière intégrale qui dans notre cas est:
Elle vaut évidemment 0 quand n est impair à cause de la symétrie par rapport à. cqfd
Bonjour
En fait c'est moi qui avait posé la question sur Futura. La réponse m'est parvenue sur Futura par un intervenant sur Futura, qui l'a posé ici, me l'a communiquée et m'a renvoyé vers votre forum pour plus d'information.
D'abord grand merci pour la réponse.
Comme cela fait partie d'un article, que je vais soumettre, je souhaiterai citer la source, comme c'est l'usage.
Actuellement j'ai mis le lien " enigmes/expression-justifier-t188467.html#p1253207", mais si l'auteur souhaite que je le cite merci de me communiquer les références par message privé.
Très cordialement
Re: Expression à justifier
Bonjour @ordage
C'est très sympa de tenir compte de notre travail (@lostounet, @ben and al.) . En effet c'est bien moi qui t'ai donné la réponse (j'ai d'autres pseudos sur les autres forums. Au passage j'en profite pour dire que j'ai une petite préférence pour ce forum. Néanmoins sur futura il y a des gens très bien ). Pour flatter mon ego, j'aimerais bien que tu mettes un petit mot à la fin de ton article et je te donne mes références en message privé.
Cela me plairait aussi que tu m' envoies ton travail. Ayant l'habitude d'être rapporteur d'articles, je pourrais éventuellement (si j'ai assez de temps) faire quelques petites remarques. Tu fais une thèse ou quoi?
C'est très sympa de tenir compte de notre travail (@lostounet, @ben and al.) . En effet c'est bien moi qui t'ai donné la réponse (j'ai d'autres pseudos sur les autres forums. Au passage j'en profite pour dire que j'ai une petite préférence pour ce forum. Néanmoins sur futura il y a des gens très bien ). Pour flatter mon ego, j'aimerais bien que tu mettes un petit mot à la fin de ton article et je te donne mes références en message privé.
Cela me plairait aussi que tu m' envoies ton travail. Ayant l'habitude d'être rapporteur d'articles, je pourrais éventuellement (si j'ai assez de temps) faire quelques petites remarques. Tu fais une thèse ou quoi?
Re: Expression à justifier
Bonjour
J'ai regardé sur ma boite de messages privés , je n'ai pas trouvé ton message avec les informations que tu décris.
Pas de problème pour t'envoyer l'article et tes commentaires sont bienvenus.
Ce projet article fait suite à une thèse que j'ai soutenue en 2013 à Paris-diderot: "Painlevé et la relativité générale".
En fait j'utilise une des idées de Painlevé (évoquée en une ligne, notamment dans un CR de l'académie des sciences du 1er Mai 1922) que j'avais remarquée, qu'il n'avait pas développée (il est retourné à sa carrière politique à l'époque) dont le développement permet de trouver une solution analytique à un problème, qui par les méthodes habituelles n'en a pas (à ma connaissance).
Bien que ce soit un problème de relativité générale, c'est 90% de maths.
Dès que j'ai les informations sur mon compte privé, je t'envoie le projet et je joindrai tes références et commentaires..
Merci
Très cordialement
J'ai regardé sur ma boite de messages privés , je n'ai pas trouvé ton message avec les informations que tu décris.
Pas de problème pour t'envoyer l'article et tes commentaires sont bienvenus.
Ce projet article fait suite à une thèse que j'ai soutenue en 2013 à Paris-diderot: "Painlevé et la relativité générale".
En fait j'utilise une des idées de Painlevé (évoquée en une ligne, notamment dans un CR de l'académie des sciences du 1er Mai 1922) que j'avais remarquée, qu'il n'avait pas développée (il est retourné à sa carrière politique à l'époque) dont le développement permet de trouver une solution analytique à un problème, qui par les méthodes habituelles n'en a pas (à ma connaissance).
Bien que ce soit un problème de relativité générale, c'est 90% de maths.
Dès que j'ai les informations sur mon compte privé, je t'envoie le projet et je joindrai tes références et commentaires..
Merci
Très cordialement
Re: Expression à justifier
aviateur a écrit:Bonjour @ordage
C'est très sympa de tenir compte de notre travail (@lostounet, @ben and al.) . En effet c'est bien moi qui t'ai donné la réponse (j'ai d'autres pseudos sur les autres forums. Au passage j'en profite pour dire que j'ai une petite préférence pour ce forum. Néanmoins sur futura il y a des gens très bien ). Pour flatter mon ego, j'aimerais bien que tu mettes un petit mot à la fin de ton article et je te donne mes références en message privé.
Cela me plairait aussi que tu m' envoies ton travail. Ayant l'habitude d'être rapporteur d'articles, je pourrais éventuellement (si j'ai assez de temps) faire quelques petites remarques. Tu fais une thèse ou quoi?
Rebonjour
J'ai bien reçu ton message, j'ai intégré tes références, mais étant nouveau membre je ne peux pas envoyer de message privé, et je n'ai pas vu dans le message reçu, où répondre au tien.
Très cordialement
Re: Expression à justifier
@Ordage: après vérification je ne vois pas de problème normalement tu as les permissions pour envoyer des MP à présent
Quel est le message d'erreur affiché?
Quel est le message d'erreur affiché?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
