Quel est le minimum d'expression
Résoudre sans dérivés partielles.
Cordialement,
Dacu
Minimum d'une expression
3 messages
- Page 1 sur 1
Minimum d'une expression
par Dacu » 05 Mar 2017, 17:01
Bonjour à tous,
Quel est le minimum d'expression
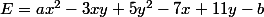
où 
.
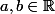
Résoudre sans dérivés partielles.
Cordialement,
Dacu
Quel est le minimum d'expression
Résoudre sans dérivés partielles.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Minimum d'une expression
par Ben314 » 05 Mar 2017, 17:30
Salut,
Y'a pas besoin de dérivées partielles vu que c'est du second degré et que la forme canonique c'est (normalement) vu au début du Lycée :
^2+(a-\frac{9}{20})x^2-\frac{37}{10}x-\frac{121}{20}-b)
Si
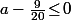
il n'y a pas de minimum (si c'est nul, le 
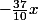
n'a pas de min.). Si 
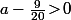
alors
^2+(a-\frac{9}{20})\big(x-\frac{37}{20a-9}\big)^2-\frac{1369}{20(20a-9)} -b-\frac{121}{20})
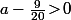
Et le minimum dans ce cas () est donc } -b-\frac{121}{20})
Et il est atteint pour l'unique)
tel que 
Y'a pas besoin de dérivées partielles vu que c'est du second degré et que la forme canonique c'est (normalement) vu au début du Lycée :
Si
Et le minimum dans ce cas (
Et il est atteint pour l'unique
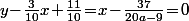
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Minimum d'une expression
par Dacu » 06 Mar 2017, 08:10
Bonjour,
Elégant! J'ai fait avec des dérivées partielles...
Merci beaucoup!
Cordialement,
Dacu
Elégant! J'ai fait avec des dérivées partielles...
Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :