Evènement de proba nulle non impossible
58 messages
- Page 3 sur 3 - 1, 2, 3
Re: Evènement de proba nulle non impossible
saluto bonjourno
excusez je vais poser ma question en français:
un ami qui me veut du bien m'a dit:
"
D'où sors-tu cela ? Si on prend la mesure de probabilité uniforme sur [0,1], alors les événements x=0,22 et x<1/2 sont indépendants. Mais ça ne veut absolument pas dire que la probabilité de x<1/2 sachant que x= 0,22 est 1/2 ; cette phrase sort de ton imagination, elle n'a absolument rien de mathématique : la probabilité de x<1/2 sachant que x= 0,22 n'existe pas vu que l'événement x=0.22 est de probabilité nulle.
Changeons maintenant de mesure de probabilité sur [0,1] : on prend la mesure qui charge chaque point k/100 avec 0<=k<=100 avec la probabilité 1/101. Alors les événements x=0.22 et X<1/2 ne sont plus indépendants, et la probabilité de x<1/2 sachant que x= 0,22 est maintenant 1"
où est la dedans votre : "le statistiquement indépendant qui est logiquement non indépendant."
remerciements…
beagle
excusez je vais poser ma question en français:
un ami qui me veut du bien m'a dit:
"
D'où sors-tu cela ? Si on prend la mesure de probabilité uniforme sur [0,1], alors les événements x=0,22 et x<1/2 sont indépendants. Mais ça ne veut absolument pas dire que la probabilité de x<1/2 sachant que x= 0,22 est 1/2 ; cette phrase sort de ton imagination, elle n'a absolument rien de mathématique : la probabilité de x<1/2 sachant que x= 0,22 n'existe pas vu que l'événement x=0.22 est de probabilité nulle.
Changeons maintenant de mesure de probabilité sur [0,1] : on prend la mesure qui charge chaque point k/100 avec 0<=k<=100 avec la probabilité 1/101. Alors les événements x=0.22 et X<1/2 ne sont plus indépendants, et la probabilité de x<1/2 sachant que x= 0,22 est maintenant 1"
où est la dedans votre : "le statistiquement indépendant qui est logiquement non indépendant."
remerciements…
beagle
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
Pourquoi refuses-tu de donner des éclaircissements sur ce que tu veux dire par "situation 1", "situation 2", "échanger" ?
PS. Pour éviter à certains de lire de travers, je précise qu'il faut lire :"la probabilité de (x<1/2 sachant que x= 0,22) n'existe pas vu que l'événement x=0.22 est de probabilité nulle."
PS. Pour éviter à certains de lire de travers, je précise qu'il faut lire :"la probabilité de (x<1/2 sachant que x= 0,22) n'existe pas vu que l'événement x=0.22 est de probabilité nulle."
Modifié en dernier par GaBuZoMeu le 09 Juil 2019, 16:04, modifié 1 fois.
Re: Evènement de proba nulle non impossible
GaBuZoMeu a écrit:Pourquoi refuses-tu de donner des éclaircissements sur ce que tu veux dire par "situation 1", "situation 2", "échanger" ?
je ne suis pas dans une situation de demande.
je ne demande pas d'aide.
je vais bien et le fil peut s'arréter là.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
C'est moi qui te demandais une aide pour comprendre ce que tu veux dire - aide que tu refuses.
Bon, d'accord. Aucune discussion un peu sérieuse n'est possible avec toi, tu viens d'en administrer une magnifique preuve. Essayer de comprendre ce que tu veux dire quand tu écris quelque chose est vain.
Bon, d'accord. Aucune discussion un peu sérieuse n'est possible avec toi, tu viens d'en administrer une magnifique preuve. Essayer de comprendre ce que tu veux dire quand tu écris quelque chose est vain.
Re: Evènement de proba nulle non impossible
Je suis d'accord avec GBZM, j'ai eu l'impression que tu essayais d'avoir un dialogue mais tu es repartit dans tes discours sans queue ni tête...
proba etre entre 0 et 0,5 sachant que x= 0,22 est 1/2 et aussi 1/2 d'etre dans 0,5 à 1
Personne n'a dis cela.
- On a dis que deux évènements était indépendants.
- On a dis que la proba conditionelle par rapport à un évènement de mesure nul n'était pas défini (certains auteurs la définisse égale à 0).
Ce qui s'en rapproche le plus c'est la notion de loi conditionelle.
- Personne n'a parlé de "1/2" pour je ne sais trop quoi.
La question que tu poses aux italiens n'a aucun sens :
- ils proposent une autre définition de l'indépendance
- les évènements {X=0.22} et {X < 0.5} ne seront pas indépendant pour leur définition (si j'ai bien compris)
Et ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Evènement de proba nulle non impossible
salut Sylviel, reponse non
Les italiens partent d'un constatde la définition normale classique.
Puis proposent.
Vous faites ce que vous voulez de leur proposition nouvelle.
Mais revenez sur leur constat et expliquez avec un exemple pourquoi ils disent c'est indépendant statistiquement alors que logiquement non indépendant.
pas à moi de démontrer l'affirmation des italiens, c'est en effet comme cela que je le comprends, mais permettez, a vous de l'expliquer.
Sur le truc x dans 0 à 1 evenement A et x dans 0à 0,5 de proba 1:2 évènement B, qui sont indépendants
redemandez l'intitulé exact à skullkid tout a été effacé
cela revenait a dire que …
donc conclusion de Skullkid on va appeler cela des évènements jaunes car ce n'est pas l'indépendance classique...
mais mince je ne cherche pas plus que les italiens,
vous ne traduisez toujours pas leur pensée…
perso je veux bien en rester là si vous ne savez pas, merci.
Les italiens partent d'un constatde la définition normale classique.
Puis proposent.
Vous faites ce que vous voulez de leur proposition nouvelle.
Mais revenez sur leur constat et expliquez avec un exemple pourquoi ils disent c'est indépendant statistiquement alors que logiquement non indépendant.
pas à moi de démontrer l'affirmation des italiens, c'est en effet comme cela que je le comprends, mais permettez, a vous de l'expliquer.
Sur le truc x dans 0 à 1 evenement A et x dans 0à 0,5 de proba 1:2 évènement B, qui sont indépendants
redemandez l'intitulé exact à skullkid tout a été effacé
cela revenait a dire que …
donc conclusion de Skullkid on va appeler cela des évènements jaunes car ce n'est pas l'indépendance classique...
mais mince je ne cherche pas plus que les italiens,
vous ne traduisez toujours pas leur pensée…
perso je veux bien en rester là si vous ne savez pas, merci.
Modifié en dernier par beagle le 09 Juil 2019, 18:50, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
la question est pourtant en tete de page je reprends l'énoncé de GBMZ et je pose la question
la-dedans où est le statistiquement indépendant mais logiquement non indépendant.
Pourquoi Sylviel tu ne demandes pas à GBMZ une phrase du genre beagle te demande … et tu ne réponds pas:
D'où sors-tu cela ? Si on prend la mesure de probabilité uniforme sur [0,1], alors les événements x=0,22 et x<1/2 sont indépendants. Mais ça ne veut absolument pas dire que la probabilité de x<1/2 sachant que x= 0,22 est 1/2 ; cette phrase sort de ton imagination, elle n'a absolument rien de mathématique : la probabilité de x<1/2 sachant que x= 0,22 n'existe pas vu que l'événement x=0.22 est de probabilité nulle.
Changeons maintenant de mesure de probabilité sur [0,1] : on prend la mesure qui charge chaque point k/100 avec 0<=k<=100 avec la probabilité 1/101. Alors les événements x=0.22 et X<1/2 ne sont plus indépendants, et la probabilité de x<1/2 sachant que x= 0,22 est maintenant 1"
où est la dedans votre : "le statistiquement indépendant qui est logiquement non indépendant."
remerciements…
beagle
la-dedans où est le statistiquement indépendant mais logiquement non indépendant.
Pourquoi Sylviel tu ne demandes pas à GBMZ une phrase du genre beagle te demande … et tu ne réponds pas:
D'où sors-tu cela ? Si on prend la mesure de probabilité uniforme sur [0,1], alors les événements x=0,22 et x<1/2 sont indépendants. Mais ça ne veut absolument pas dire que la probabilité de x<1/2 sachant que x= 0,22 est 1/2 ; cette phrase sort de ton imagination, elle n'a absolument rien de mathématique : la probabilité de x<1/2 sachant que x= 0,22 n'existe pas vu que l'événement x=0.22 est de probabilité nulle.
Changeons maintenant de mesure de probabilité sur [0,1] : on prend la mesure qui charge chaque point k/100 avec 0<=k<=100 avec la probabilité 1/101. Alors les événements x=0.22 et X<1/2 ne sont plus indépendants, et la probabilité de x<1/2 sachant que x= 0,22 est maintenant 1"
où est la dedans votre : "le statistiquement indépendant qui est logiquement non indépendant."
remerciements…
beagle
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
On peut avoir des événements  et
et  avec
avec 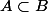 et
et  et
et  indépendants au sens probabiliste. Ceci se produit pour toute mesure de probabilité telle que
indépendants au sens probabiliste. Ceci se produit pour toute mesure de probabilité telle que  = 1) ou telle que
ou telle que =0) .
.
Cela peut heurter les âmes sensibles, mais il n'y a certainement pas là d'inconsistance mathématique
Cela peut heurter les âmes sensibles, mais il n'y a certainement pas là d'inconsistance mathématique
Re: Evènement de proba nulle non impossible
GaBuZoMeu a écrit:On peut avoir des événementset
avec
et
et
indépendants au sens probabiliste. Ceci se produit pour toute mesure de probabilité telle que
ou telle que
.
Cela peut heurter les âmes sensibles, mais il n'y a certainement pas là d'inconsistance mathématique
a l'évidence l'article mis en ligne date de 1998 et on n'a pas noté un changement de définition des évenements indépendants. Donc c'est que les maths et les mathématciens vivent très bien avec ça.
Oui!
Ensuite si ètre sensible c'est donner du sens, alors il n'est pas inintéressant de regarder à quoi on joue.
Et s'agissant des probas nulles j'espère que tout le monde a bien suivi la différence de sens entre les deux types de probas nulles qui existent s'agissant de leur répercussion sur la déclaration de l'indépendance.
Maintenant pour discuter, cela ne peut se faire qu'en confiance. Donc désolé auprès des lecteurs, désolé auprès des modos, lorsque la confiance n'est pas là je mets des systèmes de protection, donc avec le firewall les discussions peuvent ètre moins claires. Mais il faut bien comprendre que je ne suis pas mathématicien de base. Par contre dans mon boulot je suis capable d'avoir une opinion tout en étant capable de développer les arguments pour et contre des opinions adverses. On (enfin je) se demande si c'est bien le cas de tout le monde sur maths forum.
Donc je ferais mon petit résumé, ma petite discussion sur les probas indépendantes un jour sur le site de mon ami Pierre. Voilà juste pour vous faire comprendre le pourquoi.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
Tes messages ne sont toujours pas très clair...
J'explicite GBZM :
Oui
{X = 0.22} et {X <0.5} (pour X uniforme sur [0,1]) sont deux évènements indépendants au sens probabiliste
Oui
{X = 0.22} implique {X < 0.5}
Par contre on ne parle pas de P(X < 0.5 | X = 0.22), que tu as dis être égal à 1/2.
Cela est déroutant en terme d'interprétation, mais ne pose pas de problème ni mathématiquement (ce sont les proba qu'on utilise depuis un bon siècle) ni en pratique (car on va toujours considérer des évènements de probabilité non-nulle).
Les italiens ont donc proposé une nouvelle notion d'indépendance plus cohérente avec l'interprétation intuitive. Pour le moment elle ne semble pas avoir convaincu la communauté mathématique. Je reconnais ne pas savoir ce qu'utiliser cette définition changerait pour les différents résultats connus.
J'ai l'impression qu'une variable aléatoire étant une classe d'équivalence à égalité presque sûre près, la notion d'indépendance de variable aléatoire resterais la même. Par contre si on revient sur la définition de variable aléatoire comme classe d"équivalence (pour les définir comme une fonction) on casse un certain nombre de choses...
J'explicite GBZM :
Oui
{X = 0.22} et {X <0.5} (pour X uniforme sur [0,1]) sont deux évènements indépendants au sens probabiliste
Oui
{X = 0.22} implique {X < 0.5}
Par contre on ne parle pas de P(X < 0.5 | X = 0.22), que tu as dis être égal à 1/2.
Cela est déroutant en terme d'interprétation, mais ne pose pas de problème ni mathématiquement (ce sont les proba qu'on utilise depuis un bon siècle) ni en pratique (car on va toujours considérer des évènements de probabilité non-nulle).
Les italiens ont donc proposé une nouvelle notion d'indépendance plus cohérente avec l'interprétation intuitive. Pour le moment elle ne semble pas avoir convaincu la communauté mathématique. Je reconnais ne pas savoir ce qu'utiliser cette définition changerait pour les différents résultats connus.
J'ai l'impression qu'une variable aléatoire étant une classe d'équivalence à égalité presque sûre près, la notion d'indépendance de variable aléatoire resterais la même. Par contre si on revient sur la définition de variable aléatoire comme classe d"équivalence (pour les définir comme une fonction) on casse un certain nombre de choses...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Evènement de proba nulle non impossible
si au départ x est pris dans [0,1]
p(x<0,5) est 1/2
et oui heureusement que vous ne le dites pas,
c'est juste qu'on l'entend très fort,
puisque indépendant, ce qui fait compréhension de l'indépendance, chuchote à l'oreille que sachant x=0,22 ,
la proba p(x<0,5) est la même et reste à 1/2.
Donc oui on peut vivre avec une définition de l'indépendance, celle du p(AinterB) =... qui fait semblant de ne pas poser problème pour les probas nulles. En effet elle ne pose pas de problème mathématique, sinon une réponse aurait été apportée, on aurait fait autrement.
p(x<0,5) est 1/2
et oui heureusement que vous ne le dites pas,
c'est juste qu'on l'entend très fort,
puisque indépendant, ce qui fait compréhension de l'indépendance, chuchote à l'oreille que sachant x=0,22 ,
la proba p(x<0,5) est la même et reste à 1/2.
Donc oui on peut vivre avec une définition de l'indépendance, celle du p(AinterB) =... qui fait semblant de ne pas poser problème pour les probas nulles. En effet elle ne pose pas de problème mathématique, sinon une réponse aurait été apportée, on aurait fait autrement.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
on l'entend très fort
Tu ne devrais pas écrire "on" mais "je".
Et encore une fois, une probabilité conditionnelle ne fait pas sens quand la probabilité de la condition est nulle.
Après, on peut chercher des théories donnant un sens à la probabilité conditionnelle quand la probabilité de la condition est nulle.
Tiens, une façon de faire qui est (peut-être) différente de ce que font les italiens.
On part d'un univers
Si
Mais si
Re: Evènement de proba nulle non impossible
Le "on" ce sont tous les gens qui font un:" OH, my god"
donc "je", donc" les italiens" , donc "Skullkid" qui sera cohérent, une autre cohérence que celle de Ben314, mais je reconnais à Skullkid une cohérence, il dira Skullkid ce n'est pas indépendant au sens du terme commun employé. Ce qui signifie également la formule est première, et après mettez le sens ou le nom que vous voulez, type évènements jaunes. Je me suis opposé à cette vision mais elle est cohérente.
En fait pour un non mathématicien comme moi, c'est d'abord ce que l'on cherche qui a créé les formules pour les calculer.Lorsqu'on analyse deux évènement A et B, je l'ai écrit ailleurs tout tombe, il n' y apas moyen d'inventer des trucs, la définition de l'indépendance tombe avec sa formule, les formules de proba conditionnelles tombent.
Les mathématiciens eux pensent que leur formule est premiere. La formule de l'indépendance doit entrainer le sens qui est derrière.La formule de sprobas conditionnelles idem.
Bon n'étant pas mathématicien je n'ai pas besoin de diviser par zéro pour calculer proba que 0,22 soit dans [0,0.5], je dis c'est 1, merci au revoir sujet suivant!
x=0,22, proba (x<0.5) = 1 plus exactement.
donc "je", donc" les italiens" , donc "Skullkid" qui sera cohérent, une autre cohérence que celle de Ben314, mais je reconnais à Skullkid une cohérence, il dira Skullkid ce n'est pas indépendant au sens du terme commun employé. Ce qui signifie également la formule est première, et après mettez le sens ou le nom que vous voulez, type évènements jaunes. Je me suis opposé à cette vision mais elle est cohérente.
En fait pour un non mathématicien comme moi, c'est d'abord ce que l'on cherche qui a créé les formules pour les calculer.Lorsqu'on analyse deux évènement A et B, je l'ai écrit ailleurs tout tombe, il n' y apas moyen d'inventer des trucs, la définition de l'indépendance tombe avec sa formule, les formules de proba conditionnelles tombent.
Les mathématiciens eux pensent que leur formule est premiere. La formule de l'indépendance doit entrainer le sens qui est derrière.La formule de sprobas conditionnelles idem.
Bon n'étant pas mathématicien je n'ai pas besoin de diviser par zéro pour calculer proba que 0,22 soit dans [0,0.5], je dis c'est 1, merci au revoir sujet suivant!
x=0,22, proba (x<0.5) = 1 plus exactement.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
beagle a écrit:Bon n'étant pas mathématicien je n'ai pas besoin de diviser par zéro pour calculer proba que 0,22 soit dans [0,0.5], je dis c'est 1, merci au revoir sujet suivant!
x=0,22, proba (x<0.5) = 1 plus exactement.
Et c'est vrai. 0.22 est inférieur à 0.5. Par contre ce qui n'existe pas, de manière classique, c'est P(X < 0.5 | X = 0.22) si X est une loi uniforme sur [0,1] sous P.
Ce qui est vrai aussi c'est que, pour tout eps (suffisemment petit), e.g. précision machine,
P(X < 0.5 | 0.22 - eps < X < 0.22 + eps) = 1.

Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Evènement de proba nulle non impossible
@Beagle: Je constate que tu te revendiques non mathématicien quand ça t'arrange et que tu veux fuir une discussion technique sur des notions précises, mais par ailleurs tu es vexé et que tu m'en veux à mort quand je te dis que ce que tu écris, ce n'est pas des mathématiques. Bon, pas grave.
Pour poursuivre la piste de mon message ci-dessus, on peut prendre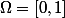 avec la tribu des ensembles Lebesgue mesurables et
avec la tribu des ensembles Lebesgue mesurables et 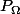 donné par la mesure de Lebesgue. Et puis, pour
donné par la mesure de Lebesgue. Et puis, pour  une partie finie non vide de
une partie finie non vide de  (donc de mesure de Lebesgue nulle), définir
(donc de mesure de Lebesgue nulle), définir ) où
où 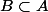 par
par 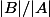 (
( voulant dire cardinal). La condition
voulant dire cardinal). La condition =P_A(B)P_B(C)) est évidemment vérifiée.
est évidemment vérifiée.
Alors, suivant la définition que j'ai donnée plus haut, la probabilité que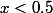 sachant que
sachant que 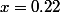 est égale à 1, et la probabilité que
est égale à 1, et la probabilité que 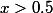 sachant que
sachant que 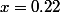 est égale à 0.
est égale à 0.
Tu devrais être content avec ça, Beagle.
Pour poursuivre la piste de mon message ci-dessus, on peut prendre
Alors, suivant la définition que j'ai donnée plus haut, la probabilité que
Tu devrais être content avec ça, Beagle.
Re: Evènement de proba nulle non impossible
N'empèche que c'est du théatre de boulevard,
la belle -mère ne devait pas venir ce week-end,
oui mais elle est là assise dans le salon.
le mari ne devait jamais rentrer avant 19h30, oui mais je l'entends rentrer,
cache toi dans le placard
0,22 ne devait jamais sortir,
oui mais c'est lui qu'est dans le placard!
alors oui, on reste bien cadré dans les définitions et la maison mathématique ne s'écroule pas,
mais c'est du théatre!
Et je ne m'oppose pas à ce que les mathématiciens tiennent la maison,
je leur demande juste un peu de second degré sur leurs équations.
la belle -mère ne devait pas venir ce week-end,
oui mais elle est là assise dans le salon.
le mari ne devait jamais rentrer avant 19h30, oui mais je l'entends rentrer,
cache toi dans le placard
0,22 ne devait jamais sortir,
oui mais c'est lui qu'est dans le placard!
alors oui, on reste bien cadré dans les définitions et la maison mathématique ne s'écroule pas,
mais c'est du théatre!
Et je ne m'oppose pas à ce que les mathématiciens tiennent la maison,
je leur demande juste un peu de second degré sur leurs équations.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
"Alors, suivant la définition que j'ai donnée plus haut, la probabilité que sachant que est égale à 1, et la probabilité que sachant que est égale à 0.
Tu devrais être content avec ça, Beagle."
en effet c'est bien ce truc!
bravo!
car je vois bien que c'est pour faire plaisir
Donc merci.
Tu devrais être content avec ça, Beagle."
en effet c'est bien ce truc!
bravo!
car je vois bien que c'est pour faire plaisir
Donc merci.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Evènement de proba nulle non impossible
Bon, j'ai fait l'erreur de passer voir le forum de 'ton ami Pierre'  . Je vois qu'il n'a toujours pas compris ce qu'on lui a expliqué patiemment sur son problème de stock. Je vais en profiter pour mettre en exemple pourquoi cette question d'évènement de proba nulle ne pose pas de problème en pratique.
. Je vois qu'il n'a toujours pas compris ce qu'on lui a expliqué patiemment sur son problème de stock. Je vais en profiter pour mettre en exemple pourquoi cette question d'évènement de proba nulle ne pose pas de problème en pratique.
Donc l'énoncé, en substance, dis "je sais que j'aurais 27 demandes dans l'année, re-remplir mon stock après une demande prends 30 jours, quel stock me faut-il pour ne jamais être en défaut".
Tout d'abord il faut définir la loi de proba des demandes. A défaut de mieux on suppose des demandes indépendantes uniforme sur les 365 jours de l'année.
Calculons la proba que les 27 demandes arrivent le premier jour de l'année :
- pour chaque demande la proba est de 1/365
- elles sont indépendantes donc la proba que toutes les demandes arrivent le premier jour est donc
^{27} \approx 10^{-69} \neq 0)
Cet évènement est de probabilité extrêmement faible, mais non nulle :
- d'un point de vue pratique il n'a aucune chance d'arriver (nombre de secondes depuis le big bang 10^17...).
- d'un point de vue mathématique, n'étant pas nul, on peut conditionner par rapport à lui. Et donc la proba d'être en rupture de stock sachant que les 27 sont arriver le premier jour de l'année est bien de 1, et tu n'as pas de problème de cohérence.
Bon, une fois de plus que bien sûr personne ne recommande d'avoir, en pratique, un stock de 27
En revanche pour dire quelque chose de raisonneble il faut :
1) modéliser les aléas
(je recommande un processus de Poisson de paramètre lambda= 27/365)
2) préciser ce que l'on entends par "ne jamais être en rupture de stock"
(je recommande une contrainte en proba de l'ordre de 5%, mais cela dépends de la criticité du stock)
avant de faire les calculs.
Pour une application la simulation sera plus rapide que le calcul exact.
Edit : j'ai fait la simulation avec la loi uniforme (27 date choisit de manière indépendantes uniformément sur l'année) et avec un processus de Poisson d'espérance 27 sur l'année : https://repl.it/repls/UnripeStaticService
dans les deux cas, sauf erreur d'implémentation, un stock initial de 8 donne entre 1 et 2% des cas où on arrive en rupture, un stock initial de 7 donne plus de 5% de chance d'être en rupture.
Donc conclusion :
- sans info supplémentaires la seule réponse possible à cet énoncé est 27 (qui fonctionne pour toute loi donnant exactement 27 durant l'année d'ailleurs).
- si on modifie légèrement l'énoncé, en précisant la loi de proba (uniforme ou Poisson par exemple), et en changeant "ne pas tomber en rupture de stock" par avoir moins de 5% de chance de tomber en rupture de stock la réponse est 8 (sauf erreur d'implémentation dans le code ci-dessus).
 . Je vois qu'il n'a toujours pas compris ce qu'on lui a expliqué patiemment sur son problème de stock. Je vais en profiter pour mettre en exemple pourquoi cette question d'évènement de proba nulle ne pose pas de problème en pratique.
. Je vois qu'il n'a toujours pas compris ce qu'on lui a expliqué patiemment sur son problème de stock. Je vais en profiter pour mettre en exemple pourquoi cette question d'évènement de proba nulle ne pose pas de problème en pratique.Donc l'énoncé, en substance, dis "je sais que j'aurais 27 demandes dans l'année, re-remplir mon stock après une demande prends 30 jours, quel stock me faut-il pour ne jamais être en défaut".
Tout d'abord il faut définir la loi de proba des demandes. A défaut de mieux on suppose des demandes indépendantes uniforme sur les 365 jours de l'année.
Calculons la proba que les 27 demandes arrivent le premier jour de l'année :
- pour chaque demande la proba est de 1/365
- elles sont indépendantes donc la proba que toutes les demandes arrivent le premier jour est donc
Cet évènement est de probabilité extrêmement faible, mais non nulle :
- d'un point de vue pratique il n'a aucune chance d'arriver (nombre de secondes depuis le big bang 10^17...).
- d'un point de vue mathématique, n'étant pas nul, on peut conditionner par rapport à lui. Et donc la proba d'être en rupture de stock sachant que les 27 sont arriver le premier jour de l'année est bien de 1, et tu n'as pas de problème de cohérence.
Bon, une fois de plus que bien sûr personne ne recommande d'avoir, en pratique, un stock de 27

En revanche pour dire quelque chose de raisonneble il faut :
1) modéliser les aléas
(je recommande un processus de Poisson de paramètre lambda= 27/365)
2) préciser ce que l'on entends par "ne jamais être en rupture de stock"
(je recommande une contrainte en proba de l'ordre de 5%, mais cela dépends de la criticité du stock)
avant de faire les calculs.
Pour une application la simulation sera plus rapide que le calcul exact.
Edit : j'ai fait la simulation avec la loi uniforme (27 date choisit de manière indépendantes uniformément sur l'année) et avec un processus de Poisson d'espérance 27 sur l'année : https://repl.it/repls/UnripeStaticService
dans les deux cas, sauf erreur d'implémentation, un stock initial de 8 donne entre 1 et 2% des cas où on arrive en rupture, un stock initial de 7 donne plus de 5% de chance d'être en rupture.
Donc conclusion :
- sans info supplémentaires la seule réponse possible à cet énoncé est 27 (qui fonctionne pour toute loi donnant exactement 27 durant l'année d'ailleurs).
- si on modifie légèrement l'énoncé, en précisant la loi de proba (uniforme ou Poisson par exemple), et en changeant "ne pas tomber en rupture de stock" par avoir moins de 5% de chance de tomber en rupture de stock la réponse est 8 (sauf erreur d'implémentation dans le code ci-dessus).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
58 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
