Résoudre dans N :
Bonne chance !
Equation diophantienne - Olympiade russe
5 messages
- Page 1 sur 1
Equation diophantienne - Olympiade russe
par Zweig » 17 Juin 2008, 12:51
Yo,
Résoudre dans N :
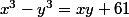
Bonne chance !
Résoudre dans N :
Bonne chance !
par lapras » 17 Juin 2008, 13:01
Salut,
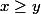
le cas
est impossible
on a
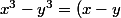(x^2 + xy + y^2) = xy + 61)
or 
=>
=> 
=> 
=> 
on a 6 cas à tester :happy2:
le cas
on a
on a 6 cas à tester :happy2:
par lapras » 17 Juin 2008, 16:54
Il suffit de remarquer l'identité :
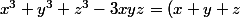(x^2 + y^2 + z^2 - xy - yz -zx))
Puis multiplier par 27 et faire apparaitre le coefficient -1 en guise de z.
:ptdr:
Puis multiplier par 27 et faire apparaitre le coefficient -1 en guise de z.
:ptdr:
par Weensie » 03 Aoû 2008, 23:22
bravo lapras ! ca sent bon l'identité qu'on apprend pour les olympiades :we:
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :