Soient
tel que x est premier
Résoudre :
Même équation si x non premier
Trouver tous lestels que :
Bon courage
Lapras
Equa diophantienne
26 messages
- Page 1 sur 2 - 1, 2
Equa diophantienne
par lapras » 27 Juin 2008, 00:33
Bon courage
Lapras
par Zweig » 27 Juin 2008, 01:21
Pour la première équation :
^2-(2y)^{2}\Longleftrightarrow x=(y^{2}-2y+2)(y^{2}+2y+2))
Puisque
est premier, il nous reste à résoudre les systèmes :
et
On trouve alors = {(5, -1),(5, 1)})
J'ai trouvé au passage une "généralisation" pour quelconque (fleimme de finir les calculs parcontre) :
^{2}=\left(4y(y^{2}+2)\right)^{2}+x^{2})
On reconnaît alors le grand théorème de Fermat au cas où
et on applique la théorie qui permet de trouver les solutions ... Enfin j'ai pas essayé les calculs, je ne sais pas si ça ammène à quelque chose d'intéressant.
Pour la deuxième équation, elle se réécrit comme^2 - (xy - 6)^2 = -13)
, on factorise etc .... l'exo classique.
Puisque
et
On trouve alors
J'ai trouvé au passage une "généralisation" pour
On reconnaît alors le grand théorème de Fermat au cas où
Pour la deuxième équation, elle se réécrit comme
par lapras » 27 Juin 2008, 01:27
Ok tres bien bonnes factorisations Zweig ! :++:
Pour pythagore apres c'est une autre histoire je pense que les calculs vont pas etre tres facile mais bon...
Pour pythagore apres c'est une autre histoire je pense que les calculs vont pas etre tres facile mais bon...
par lapras » 27 Juin 2008, 14:38
Il suffit de résoudre un polynome du second degré donc le discriminant est :
^2)
ce discriminant est un carré parfait, il viens deux solutions :
 = (-0,1) , (0,-1))
ce discriminant est un carré parfait, il viens deux solutions :
par lapras » 27 Juin 2008, 17:08
On peut aussi poser
on a alors
le discriminant est le même que précédemment on peut résoudre :
et
on a alors
le discriminant est le même que précédemment on peut résoudre :
et
par lapras » 27 Juin 2008, 20:45
Je l'ai déja postée sur le forum, mais beaucoup n'ont surement pas vu mon post :
Résoudre :
Résoudre :
par Zweig » 28 Juin 2008, 00:25
Oui lapras, on pouvait passer par l'Algèbre, mais on pouvait aussi rester dans de l'Arithmétique pure :
^{2}+x^{3}=y^{4})
^{2}+(x^{3}+1)=y^{4}+1)
^{2}+4(x^{3}+1)=4y^{4}+4)
+1\right)^{2}-1=(2y^{2})^2+4)
\left(2y^2+2x^3+3 \right)=-5)
etc ...
C'est effectivement plus long ...
etc ...
C'est effectivement plus long ...
par ThSQ » 28 Juin 2008, 15:07
lapras a écrit:Je l'ai déja postée sur le forum, mais beaucoup n'ont surement pas vu mon post :
Résoudre :
[size=0]IMO 06[/size] .
par lapras » 08 Juil 2008, 23:05
pas de solution pour mon équa ?
Une autre vraiment facile :
trouver tous les p, q, r, s entiers naturels tels que :
i)p et q premiers
ii)
Une autre vraiment facile :
trouver tous les p, q, r, s entiers naturels tels que :
i)p et q premiers
ii)
par Zweig » 09 Juil 2008, 02:18
T'abuses un peu sur tes "trivial", "très simple" quand même hein, il est loin d'être trivial cet exo. On va montrer que seul le couple  = (3, 2, 3 ,2))
est solution du problème.
Clairement,
ou 
est pair. Mais puisque et sont premiers, alors, sans perté de généralité, 
. Nous sommes alors ammené à résoudre 
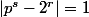
* Si
et 
sont pairs, 
et 
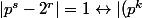, alors : ^2 - (2^n)^2| = 1 \leftrightarrow |p^k - 2^n||p^k + 2^n| = 1)
Or
, ainsi l'égalité ne peut avoir lieu.
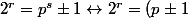* Si est impair alors (p^{m-1} \pm p^{m - 2} + \cdots - p + 1))
Or le premier facteur de droite est clairement impair et plus grand que 1, ainsi l'égalité ne peut avoir lieu. Par conséquent, est pair, 
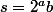
avec 
impair, et est impair.
Nous allons montrer que
:
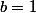
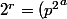^b \pm 1 \leftrightarrow 2^r = ({p^2}^a \pm 1)(({{p^2}^a})^{(b-1)} \pm \cdots - {p^2}^a + 1))
On conclut de la même manière que précédemment, ce qui implique que
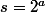
Notre équation se réécrit alors :
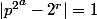
avec impair. Il nous reste alors deux cas à traiter :
Cas 1 :
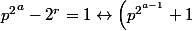\left(p^{2^{a-1}}-1\right)=2^{r})
Cette relation implique que
et 
sont des puissances de 2. Or les seules puissances de 2 espacées de 2 nombres sont 2 et 4, d'où 
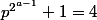
et 
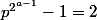
. On en tire alors 
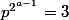
, d'où
Cas 2 :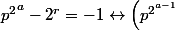
^{2} = (2 - 1)(2^{r - 1} + \cdots + 2 + 1) \equiv 3 [4])
Or un carré impair est toujours congru à 1 mod 4, d'où l'impossibilité de cette égalité.
Conclusion : L'unique couple solution est
Clairement,
* Si
Or
* Si
Or le premier facteur de droite est clairement impair et plus grand que 1, ainsi l'égalité ne peut avoir lieu. Par conséquent,
Nous allons montrer que
On conclut de la même manière que précédemment, ce qui implique que
Notre équation se réécrit alors :
Cas 1 :
Cette relation implique que
Cas 2 :
Or un carré impair est toujours congru à 1 mod 4, d'où l'impossibilité de cette égalité.
Conclusion : L'unique couple solution est
par raito123 » 09 Juil 2008, 12:38
(p,2,1,0) ; (2,q,0,1) !!
(en fait j'ai pas chercher de demo )
(en fait j'ai pas chercher de demo )
Les multiples ne doivent pas être utilisés sans nécessité
par lapras » 09 Juil 2008, 12:59
Zweig > Peutr etre as tu fait des erreurs de calcul je n'ai pas vérifié mais le raisonnement est bon (j'ai lu rapidement).
Je voulais dire par facile que le raisonnement est long mais ne demande pas d'astuces : c'est assez répétitif.
Je voulais dire par facile que le raisonnement est long mais ne demande pas d'astuces : c'est assez répétitif.
par Help » 09 Juil 2008, 16:19
Zweig, quand tu exclues le cas s impair, je crois que tu oublies le cas s=1.
Or si s=1, il y a une infinité de solution
q=2; s=1 cela donne notamment p=2^r - 1 et on a tous les nombres premiers de Mersenne qui vont être solution si je ne m'abuse.
Du coup Lapras, je me pose une question : dans ton énoncé, faut-il exclure 0 et 1 des solutions possible pour p,q,r et s ? Sinon la réponse risque d'être très compliquée à détailler.
Or si s=1, il y a une infinité de solution
q=2; s=1 cela donne notamment p=2^r - 1 et on a tous les nombres premiers de Mersenne qui vont être solution si je ne m'abuse.
Du coup Lapras, je me pose une question : dans ton énoncé, faut-il exclure 0 et 1 des solutions possible pour p,q,r et s ? Sinon la réponse risque d'être très compliquée à détailler.
par Zweig » 09 Juil 2008, 17:19
Hum, dans ma tête les nombres étaient >= 2 par rapport à ces cas, enfin plutôt celui de Mersenne .
par lapras » 09 Juil 2008, 21:35
Trouver tous les entiers x,y et n strictements positifs tels que :
i) = 1)
ii)
Exercice tres interessant :
Soit a,b entiers strictements positifs tels que
divise 
Montrer que
est un carré parfait.
i)
ii)
Exercice tres interessant :
Soit a,b entiers strictements positifs tels que
Montrer que
par Zweig » 11 Juil 2008, 00:05
lapras a écrit:Trouver tous les entiers x,y et n strictements positifs tels que :
i)
ii)
On va montrer qu'il n'existe aucune solution.
Soit
Par conséquent,
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :