Double inversion

[Chimerade]

Tout le monde sait que si l’on appuie deux fois de suite sur la touche « 1/x » d’une calculatrice, on ne retombe pas toujours sur le même nombre. Bon !
Je propose de préciser un peu les choses. Je suppose que la calculatrice affiche (et mémorise) en mode scientifique, avec 12 chiffres significatifs sous la forme x,xxxxxxxxxxx. De plus, je suppose qu’elle retient à chaque opération les douze premiers chiffres significatifs, sans opérer d’arrondi vers le haut (troncature donc).

Entre 1.00000000000 et 9.99999999999 (bornes incluses), il y a exactement 900000000000 représentations différentes de nombres, disons 900000000000 mantisses différentes. Pour combien d'entre elles la double opération consistant à appuyer deux fois de suite sur la touche « 1/x » réaffiche-t-elle le nombre initial ?

[Chimerade]

Personne pour relever le défi ?

Pour info :

Les concepts mathématiques nécessaires à la résolution de ce problème sont acquis en 3-ième. Pour ce qui est niveau de réflexion, de savoir-faire, je pense qu'un élève de TS devrait être capable de le faire... Pour un élève de prepa, c'est enfantin !

Alors...

[mathador]

Les concepts mathématiques nécessaires à la résolution de ce problème sont acquis en 3-ième. Pour ce qui est niveau de réflexion, de savoir-faire, je pense qu'un élève de TS devrait être capable de le faire... Pour un élève de prepa, c'est enfantin ! alors...

... alors c'est de la provocation
Pour la peine, je cherche

[celge]

Dis moi juste si je m'engage dans la bonne voie : je cherche à savoir si ca a un rapport avec les derniers chiffres des nombres. ??

[Chimerade]

Dis moi juste si je m'engage dans la bonne voie : je cherche à savoir si ca a un rapport avec les derniers chiffres des nombres. ??

Difficile de répondre à ta question. Il est certain que "ca a un rapport avec les derniers chiffres des nombres", puisqu'il s'agit d'arrondis ! Par contre, ma démonstration ne se focalise pas sur ce fait.

Cela dit, il n'est pas exclu que tu trouves une autre démonstration, qui, elle se focalise sur les derniers chiffres des nombres...

Ai-je répondu à ta question ?

[celge]

oui, tu as repondu parfaitement à ma question, et je t'en remercie.

[Anonyme]

j'espere ne pas dire de betises mais si l'on note 1/x=y avec une precision de 11 chiffres apres la virgule il suffit de multiplier 1/x par 10^11 et de trouver pour quels valeurs de x, y est un nombre entier. je suis en seconde et je ne dispose pas des outils arithmetiques que vous avez ...

[Chimerade]

j'espere ne pas dire de betises mais si l'on note 1/x=y avec une precision de 11 chiffres apres la virgule il suffit de multiplier 1/x par 10^11 et de trouver pour quels valeurs de x, y est un nombre entier. je suis en seconde et je ne dispose pas des outils arithmetiques que vous avez ...

Tu ne dis pas de bêtises...

[Alpha]

Entre 1.00000000000 et 9.99999999999 (bornes incluses), il y a exactement 900000000000 représentations différentes de nombres

Bien qu'étant élève de prépa, j'avoue que j'ai un peu de mal à saisir la dernière partie de l'énoncé, qui, selon moi, est assez vague dans sa formulation (mais ça peut aussi venir de moi ).

Pour moi, entre 1.00000000000 et 9.99999999999, il n'y a aucun nombre de moins de 12 chiffres, le "successeur" de 9.99999999999 étant 1.00000000000. Je ne vois donc pas à quoi correspond le nombre de représentations différentes de nombres dont tu parles.

De toute évidence, si je pense avoir très bien compris la 1ère partie de ton énoncé, je n'ai pas compris ce que tu voulais dire dans la 2ème. Quelque chose de tout bête a du m'échapper! Peux-tu m'expliquer ce que tu as voulu dire?

Merci d'avance

[mathador]

Oops, you did it again, Alpha ;)
le "successeur" de 1,00000000000 est 1,00000000001 ... le successeur de 9,99999999999 serait bien 1,00000000000 avec l'ajout d'une unité à l'ordre de grandeur, mais tu as oublié quelques autres valeurs ... par exemple 1,618 033 988 75 (arrondi à 10^-11 du nombre d'or), 3,141 592 653 59 (même principe avec pi, naturellement !) ou 2,718 281 828 46 ... Donc franchement, ç'aurait été dommage de passer à côté (on peut rajouter racine de 2, de 3, de 4 -sans intérêt- de 5 de 6 de 7 de 8 etc ...)
Et le problème résiste encore :)

[Chimerade]

Pour moi, entre 1.00000000000 et 9.99999999999, il n'y a aucun nombre de moins de 12 chiffres, le "successeur" de 9.99999999999 étant 1.00000000000. Je ne vois donc pas à quoi correspond le nombre de représentations différentes de nombres dont tu parles.

De toute évidence, si je pense avoir très bien compris la 1ère partie de ton énoncé, je n'ai pas compris ce que tu voulais dire dans la 2ème. Quelque chose de tout bête a du m'échapper! Peux-tu m'expliquer ce que tu as voulu dire?

Pour l'instant, je ne peux pas, vu que je ne comprends pas ce que tu ne comprends pas ! Est-ce que la réponse de mathador (que je remercie) t'a permis de voir s'envoler tes incertitudes ? Si oui, c'est parfait. Sinon, merci d'expliciter un peu plus, car vraiment j'ai du mal à percevoir ton problème.

Amicalement

[Alpha]

Je suis vraiment confus :

Au lieu de lire entre 1.00000000000 et 9.99999999999, je ne sais pas comment ça se fait, j'ai compris entre 0.9999999999 et 1.00000000000 ...

Forcément, ça n'aide pas...

Bon, je me suis couvert de ridicule... :o Je n'arrive pas à m'expliquer comment j'ai pu lire à ce point de travers. Ca ne m'arrive quasiment jamais. Mille excuses.

Tout s'éclaircit maintenant.

;)

[mathador]

Oui, ta honte fait ombre à toute l'équipe de modération :D
Allons, allons, c'est rien ;) tu as juste perdu toute crédibilité.
Un seul moyen de se racheter : résoudre cette énigme !!!

[pianozik]

Bon peut être j'ai pû résoudre cette énigme, voilà. Au début, j'ai négliger l'intervalle proposé mais à la fin, je me suis rendu compte qu'il a d'utilité.
Notons que tout nombre décimal est rationnel
Comme vous dites, ce nombre qu'on va noter a 12 valeurs représentatifs et il fait parti de l'intervalle [1; 9,99999999999], par conséquent le nombre admet la forme suivante (en sachant qu'il est décimal) :
, donc il existe un nombre appartenant à Z tel que
Pour le nombre on a deux cas qu'on va citer:
Cas 1°) est est rationnel avec au maximum 11 nombres après la virgule, dans ce cas
Cas 2°) est rationnel avec nombres après la virgule (que ce soit fini ou infini), puisque la calculatrice ne retient que 12 chiffres représentatifs (sans opérer d'arrondi), alors :
Or, la calculatrice retiendera que le nombre , d'où que ce nombre est plus un réel non nul
Le nombre n'est jamais irrationnel, car l'inverse d'un nombre décimal est une fraction de deux entiers qui est rationnelle
Il me reste mnt la confirmation , merci

[Chimerade]

Bonjour pianozik,

C'est un peu dur de commenter ta réponse, mais je vais essayer.

Bon peut être j'ai pû résoudre cette énigme, voilà.

Première remarque : la réponse à l'énigme est un nombre et je ne vois pas de nombre. Donc, peut-être as-tu résolu cette énigme, mais tu ne nous as pas encore dévoilé le nombre cherché.

Cas 1°) est est rationnel avec au maximum 11 nombres après la virgule, ...

Je suis d'accord que dans ce cas-là la double inversion donne un résultat exact. Cependant, d'une part on peut déplorer l'absence de démonstration (tu affirmes quelque chose qui n'est pas si évident que cela et tu ne le démontres pas), d'autre part, il faut savoir que seuls des nombres de la forme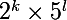 peuvent avoir cette propriété, et tous ne l'ont pas, je pense. Et le nombre de tels nombres est misérablement petit, comparé aux 900 000 000 000 de nombres dont il est question. Mais bon ! Un point pour toi !

Pour clarifier mon propos, l'appelle R(x) la représentation de x sur la calculette, ce qui veut dire que R(x) peut être différent de x, d'accord ?
Dans le cas où le développement décimal de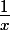 dépasse les 12 chiffres décimaux - ce qui est donc le cas général - je suis d'accord avec ton affirmation selon laquelle

D'accord, mais, j'attends la suite.
Etant donné que je désire que tu trouves la solution, je suis un peu inquiet de cette voie que tu as prise. Mais l'expérience montre qu'on peut souvent arriver à démonter la même chose par plusieurs voies différentes. Le fait que je ne voie pas comment tu peux continuer dans cette voie, ne prouve nullement que tu ne vas pas trouver un moyen : je peux me tromper.
En outre, le début de formalisation que tu as faite peut mener à d'autres pistes...Lis bien le post du 31/07/2005 à 00h11

Bon courage !

[Anonyme]

Puisque c'est a la portee d'un eleve de seconde, il n'y ni logs, ni integrations.
Puisque c'est un probleme autoreciproque, il y a une symetrie d'ordre 2.
Donc, dans un cas sur deux ca marche, et dans un cas sur deux, ca marche
pas.

La solution serai donc 450000000000.

Plus serieusement, si on multiplie le nombre original par 10^11,
on a un entier compris dans [10^11, 10^12 [
Si on multiplie son inverse par 10^12, on a un entier compris dans ]10^11, 10^12 ]
Aux problemes de bornes pres, on a donc l'inversion qui est une application
de l'intervalle [10^11, 10^12] dans lui-meme, et on cherche simplement
cardinal (image)

J'ai essaye de le determiner a partir du nombre de "non-collisions"
(cas ou un nombre et son predecesseur n'ont pas le meme inverse pour la calculette),
mais ca n'est pas si simple vu qu'il faut aussi distinguer les collisons a 2,
3, 4, etc..

Soit m la mantisse, 1/x = 10^11/m, la difference entre les inverses de deux nombres successifs est 10^11(1/m-1 - 1/m).

Il y a non-collision si 10^23 (1/(m-1)m) >1, donc si m^2-m-10^23 < 0,
m <( 1 + racine (1+4 10^23)) / 2

Il n'y a pas triple collision si 10^23(1/m-2 - 1/m)> 1, pas quadruple
si 10^23(1/m-3 - 1/m)> 1, etc.

Ca me parait bien complique.

[Chimerade]

La solution serai donc 450000000000.

NON !

Puisque c'est a la portee d'un eleve de seconde,...

Trop facile ! C'est vrai je n'aurais pas dû dire cela : c'est déjà une indication.

Tu étais sur la bonne voie... jusqu'à un certain point. Ne te fourvoie pas, tu brûles !

Il n'y a pas triple collision si 10^23(1/m-2 - 1/m)> 1, pas quadruple
si 10^23(1/m-3 - 1/m)> 1, etc.Ca me parait bien complique.

Là, ça devient compliqué, mais faut-il aller jusque là ?

[Anonyme]

Tu étais sur la bonne voie... jusqu'à un certain point. Ne te fourvoie pas, tu brûles !

Là, ça devient compliqué, mais faut-il aller jusque là ?

Non, bien sur, une fois dans mon lit j'ai vu que j'avais elimine trop vite
l'idee qu'en multipliant l'inverse par 10^11, on avait une application
de [10^11,10^12[ dans ]10^10,10^11] parce que je pensais que ca ne donnait
qu'un majorant.
Mais dans mes divagations ulterieures, il y avait la condition pour que toute valeur
de ]10^10,10^11] soit bien atteinte :
m^2 - m - 10^22 > 0, donc m > (1+racine(1+4 10^22))/2, en gros m > 10^11,
le cas 10^11 doit etre regarde separement (et on voit qu'il est bien atteint).

Donc card(image(1/x calculette)) = card (]10^10,10^11]) = 9 10^10

[pianozik]

s'il vous plait, qu'est ce qu'une mantisse ? (je suis marocain et on étudie les maths en arabe, malgré la traduction qu'on a comme matière, certains mots peuvent s'échapper)Peut si j'avais bien compris, de l'énoncé on peut dire que les mantisses est le cardinal de l'intervalle [1; 9.99999999999] (en sachant que chaque nombre a 11 chiffres après la virgule au maximum. est-ce ça ?

[Chimerade]

Non, bien sur, une fois dans mon lit j'ai vu que j'avais elimine trop vite
l'idee qu'en multipliant l'inverse par 10^11, on avait une application
de [10^11,10^12[ dans ]10^10,10^11] parce que je pensais que ca ne donnait
qu'un majorant.
Mais dans mes divagations ulterieures, il y avait la condition pour que toute valeur
de ]10^10,10^11] soit bien atteinte :
m^2 - m - 10^22 > 0, donc m > (1+racine(1+4 10^22))/2, en gros m > 10^11,
le cas 10^11 doit etre regarde separement (et on voit qu'il est bien atteint).

Donc card(image(1/x calculette)) = card (]10^10,10^11]) = 9 10^10

J'ai bien du mal à te suivre...