Divisible par 3

[guigui51250]

Pour passer le temps...

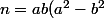Montrer que pour tout entier a et b, est divisible par 3

[le_fabien]

Bonsoir, cela doit bien se faire avec les congruences non ?

[guigui51250]

Bonsoir, cela doit bien se faire avec les congruences non ?

ouè ça se fait en 2 minutes avec les congruences

[le_fabien]

Ok ça c'est facile, mais comment faire par une autre méthode ?

[guigui51250]

Ok ça c'est facile, mais comment faire par une autre méthode ?

par une autre méthode? j'avoue que je n'y ai pas pensé

[le_fabien]

Et oui voilà l'intérêt , comment faire pour résoudre un problème de plusieurs façons. :zen: Et là je sais pas encore..

[guigui51250]

Et oui voilà l'intérêt , comment faire pour résoudre un problème de plusieurs façons. :zen: Et là je sais pas encore..

oui moi non plus je ne sais pas, je vais y réfléchir ^^

[leon1789]

n = ab(a²-b²) = ab(a-b)(a+b)

si b est multiple de 3, c'est fini,
sinon parmi a-b , a+0.b , a+b il y a un et un seul multiple de 3.

ok c'est pas loin du modulaire... :triste:

[guigui51250]

n = ab(a²-b²) = ab(a-b)(a+b)

si b est multiple de 3, c'est fini,
sinon parmi a-b , a+0.b , a+b il y a un et un seul multiple de 3.

ok c'est pas loin du modulaire... :triste:

ouè c'est de la congruence sans dire le mot congru ou modulo lol

[leon1789]

ouè c'est de la congruence sans dire le mot congru ou modulo lol

oué, mais tu pourras dire ça à chaque fois que quelqu'un dira >, non ?

[guigui51250]

oué, mais tu pourras dire ça à chaque fois que quelqu'un dira >, non ?

et ouè c'est ça le truc, à chaque fois qu'on doit montrer qu'un nombre divise un autre, il y a une histoire de congruence (même si on utilise pas toujours la congruence)

[leon1789]

Tu crois qu'on ne peut pas expliquer cela sans utiliser des congruences ?

<<
si pgcd(b,n)=1
alors parmi a+0.b, ...., a+(n-1)b , il y a un et un seul nombre divisible par n
>>

[guigui51250]

Tu crois qu'on ne peut pas expliquer cela sans utiliser des congruences ?

>

euh je n'ai pas bien compris to raisonnement, je n'ai pas encore étudier les calculs avec les pgcd (c'est pour la semaine prochaine en spé ^^)

[leon1789]

j'utilise cette propriété (pas encore démontrée certes, mais j'imagine qu'on peut le faire avec une relation de Bezout en b et n) avec n=3 pour ta question.

[guigui51250]

j'utilise cette propriété (pas encore démontrée certes, mais j'imagine qu'on peut le faire avec une relation de Bezout en b et n) avec n=3 pour ta question.

euh je n'ai pas tout saisi mais je revérais ça quand j'aurais vu ça en cours

[raito123]

j'utilise cette propriété (pas encore démontrée certes, mais j'imagine qu'on peut le faire avec une relation de Bezout en b et n) avec n=3 pour ta question.

On peut utiliser une autre propriété : parmi n+1 entier il existe deux tel que leur différence est un multiple de n !!!

Cette propriété est facilement démontrée par le lemme des tirroirs mais elle va compliquer la vie si on l'utilise dans cette exo !!

( en fait je pense que cette discution n'a pas de place dans la partie olympiade )

[lapras]

salut,
sans vouloir offenser guigui, je pense aussi que cette discussion devrait être dans lycée...(même si c'est de l'arithmétique, ca ne veut pas dire forcément olympiades)

[guigui51250]

salut,
sans vouloir offenser guigui, je pense aussi que cette discussion devrait être dans lycée...(même si c'est de l'arithmétique, ca ne veut pas dire forcément olympiades)

oui je sais très bien que ce n'ai pas de l'olympiade mais enfait je ne voulais pas mettre ça dans la partie Lycée car j'ai déjà la réponse à mon exercice, je n'ai pas besoin qu'on me le fasse, je voulais juste voir s'il y avait d'autre possibilité de faire cet exo que par la congruence alors je me suis dit que c'était dans la partie olympiade qu'il y aurait pu avoir réponse à pa demande ^^
Celà je suis tout à fait d'acord avec vous ce n'est pas un sujet d'olympiade puisque c'est ce que je fait en cours