Divisible par 3

[guigui51250]

Salut

Montrer que pour tout entier relatif , est divisible par 3.

Ouè je sais c'est trop simple mais ça occupe lol :ptdr:

PS : extrait de mon DM de spé...

[miikou]

n^3-n = n*(n²-1)= (n-1)*n*(n+1) ca parle tout seul ..

[guigui51250]

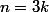
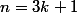
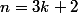
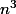
ah moi j'ai pas fait comme ça j'ai dit que tout s'écrivait sous la forme , ou et j'ai calculer dans chaque cas, je me suis encore compliqué la vie alors :marteau:

[guigui51250]

Aller comme celui là était trop facile je propose un autre problème :

Démontrez que est divisible par

Celle là je n'ai pas réussi... :mur: mais je n'ai pas encore vu la congruence :briques:

PS : issue de mon cours de spé lol

[nodgim]

Sans rien calculer, 1+2+3+4 est divisible par 5, donc les mêmes termes élevés à la puissance 2009 (4k+1) ont une somme également divisible par 5.

[miikou]

ca se fait tres bien avec les congruence ;)

[guigui51250]

ca se fait tres bien avec les congruence

tu peux me donner la solution avec les congruences stp pour que j'essaye de comprendre cette méthode

[leon1789]

tu peux me donner la solution avec les congruences stp pour que j'essaye de comprendre cette méthode

peut-être commencer par montrer que pour , on a x^4 congru à 1 modulo 5

[leon1789]

tu peux me donner la solution avec les congruences stp pour que j'essaye de comprendre cette méthode

rien de plus simple (façon de parler bien sûr...)

modulo 5, on a 4=-1 et 3=-2 et ton problème se transforme en
qui est clairement nul, donc divisible par 5 :zen:

[guigui51250]

ok merci Léon :happy2:

[acoustica]

Salut

Montrer que pour tout entier relatif , est divisible par 3.

Ouè je sais c'est trop simple mais ça occupe lol :ptdr:

PS : extrait de mon DM de spé...

Il y en a d'autres du même style:
Montrer que si n n'est pas divisible par 3, n^6-1 est divisible par 9.

ou encore:

Montrer que si n n'est pas divisible par 5, alors (n^2-1)(n^2-4) est divisible par 5.

Bien sûr, on peut toujours y aller à la disjonction de cas, mais c'est toujours mieux de faire une factorisation.
:happy2:

[guigui51250]

Bien sûr, on peut toujours y aller à la disjonction de cas, mais c'est toujours mieux de faire une factorisation.
:happy2:

Ouè mais là je n'avais pas pensé à la factorisation :marteau: j'ai tout de suite pensé à la disjonction des cas

[miikou]

(n²-1)(n²-4)=(n-1)(n-2)(n+1)(n+2) la aussi ca parle tout seul ,)

[axiome]

Sinon, pour prouver qu'une formule en n est divisible par un nombre, une récurrence fonctionne aussi à chaque fois...

[guigui51250]

Sinon, pour prouver qu'une formule en n est divisible par un nombre, une récurrence fonctionne aussi à chaque fois...

oui ma récurrence c'est pas mal, rapide et assez simple (pour des exo basiques)

[Zweig]

Dans la foulée, un classique :

Soit un entier naturel impair. Montrer que la somme



est divisible par

:++:

[guigui51250]

Dans la foulée, un classique :

Soit un entier naturel impair. Montrer que la somme



est divisible par

:++:

ah mince je l'ai vu en cours mais je ne m'en rappel plus :mur: :mur:

Une histoire de récurrence il me semble

[Zweig]

Salut

Montrer que pour tout entier relatif , est divisible par 3.

D'après le petit théorème de Fermat :

[guigui51250]

D'après le petit théorème de Fermat :

ouè mais si j'ai bien compris ce théorème ça revient à faire la disjonction des cas non?

[Zweig]

Comment ça ? Cette relation de congruence est vraie pour tout