Cubes et carrés
7 messages
- Page 1 sur 1
Re: Cubes et carrés
Salut,
Vu l'homogénéité, on peut supposer que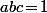 et, si on pose
et, si on pose 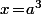 et
et 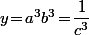 , on doit montrer que
, on doit montrer que  + \Big(x+\dfrac{y}{x}+\dfrac{1}{y}\Big))
c'est à dire (en multipliant par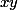 ) que le polynôme
) que le polynôme
=y^3-(x\!+\!1)y^2-(x^2\!-\!3x\!+\!1)y+(x\!+\!1)(x-1)^2)
reste positif sur quelque soit
quelque soit 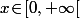
Ce qui se fait relativement bien par une simple étude de fonction vu que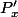 n'est que de degré 2.
n'est que de degré 2.
Vu l'homogénéité, on peut supposer que
c'est à dire (en multipliant par
reste positif sur
Ce qui se fait relativement bien par une simple étude de fonction vu que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cubes et carrés
Parce que la relation est homogène : si on multiplie a, b et c par la même constante lambda>0, ça ne change rien à l'inégalité (elle est uniquement multipliée par lambda^9).scardy123 a écrit:Pourquoi pouvez-vous définir?
Et en multipliant par un lambda convenable (en fait
Si tu préféré (ça revient bien évidement exactement au même), tu pose
P.S. : ça t'apporte quoi d'avoir les solutions de tout ces trucs d'olympiade alors qu'assez clairement, tu as pas du tout le niveau pour les chercher ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Cubes et carrés
J'aime les inégalités et les problèmes olympiques, mais je ne suis pas expert et je suis ici pour apprendre.

Re: Cubes et carrés
Ben à mon avis, tu ferais très nettement mieux de chercher des trucs plus simples que TU est capable de trouver tout seul.
Y'a un truc que je répète souvent à mes étudiant (et ça m'étonne toujours autant vu que ça semble quand même être une sacré trivialité) : les maths, c'est comme le vélo, c'est pas en regardant les autres en faire (i.e. en regardant des solutions d'exercices) qu'on apprend à en faire, c'est bien évidement en en faisant soi même.
Regarder les autres, ça peut servir pour voir des "trucs" auquel on aurait pas pensé tout seul, mais c'est évidement pas ça "la base" de l'apprentissage. La base, c'est évidement de pratiquer.
Par exemple, est-ce que tu pense que, pour quelqu'un qui tient un peu limite en équilibre sur un vélo, ça apportera quoi que ce soit de regarder les mecs pédaler sur le tour de France ? Parce que là, de voir que tu ne visualise même pas que le truc à montrer est homogène, ça me donne pas mal l'impression que c'est ce que tu fait...
Y'a un truc que je répète souvent à mes étudiant (et ça m'étonne toujours autant vu que ça semble quand même être une sacré trivialité) : les maths, c'est comme le vélo, c'est pas en regardant les autres en faire (i.e. en regardant des solutions d'exercices) qu'on apprend à en faire, c'est bien évidement en en faisant soi même.
Regarder les autres, ça peut servir pour voir des "trucs" auquel on aurait pas pensé tout seul, mais c'est évidement pas ça "la base" de l'apprentissage. La base, c'est évidement de pratiquer.
Par exemple, est-ce que tu pense que, pour quelqu'un qui tient un peu limite en équilibre sur un vélo, ça apportera quoi que ce soit de regarder les mecs pédaler sur le tour de France ? Parce que là, de voir que tu ne visualise même pas que le truc à montrer est homogène, ça me donne pas mal l'impression que c'est ce que tu fait...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

