Conserve la somme et l'inverse
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 03:14
par Nightmare » 11 Déc 2010, 03:14
Salut,
Niveau débutant en équation fonctionnelle :
Quelles sont les applications
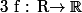
telles que
=f(x)+f(y)\\f(x^{-1})=(f(x))^{-1}\\f(1)=1)
?
Et comme ça va surement être réglé en deux secondes par les olympieux (? olympiants ? olympiques ... ?) :
- f(x+y)=f(x)+f(y) avec f : Z -> Z/nZ ?
- f(x+y)=f(x)+f(y) avec f : Z/nZ -> Z/mZ ?
:happy3:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 11 Déc 2010, 11:27
par vincentroumezy » 11 Déc 2010, 11:27
Bonjour, matinal ?
Je pense à l'application identité, défini par f(x)=x.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Déc 2010, 12:16
par Doraki » 11 Déc 2010, 12:16
Pour le 1,
Une fois qu'on a trouvé xy = 1/(2/(1+x-y) +2/(1-x+y)) - 1/(2/(1+x+y) +2/(1-x-y)), ça devient tout de suite plus facile
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 12:27
par Nightmare » 11 Déc 2010, 12:27
vincent > Elle la vérifie, c'est sûr, est-ce la seule ?
Doraki > J'ai pas du tout utilisée cette astuce et je ne vois pas trop ce que tu en ferais, si tu veux détailler.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Déc 2010, 12:34
par ffpower » 11 Déc 2010, 12:34
A mettre en lien avec un de mes tous premiers topics du forum : :we:
http://www.maths-forum.com/l-art-multiplier-multiplications-52114.phpHistoire de récupérer le f(xy)=f(x)f(y)
On peut éventuellement simplifier un peu en ce contentant de x²=x+(1/(x-1)-1/x)^{-1}, qui permet de récupérer f(x²)=f(x)², ce qui suffit pour récupérer la monotonie
-
Anonyme
 par Anonyme » 11 Déc 2010, 12:42
par Anonyme » 11 Déc 2010, 12:42
Bonjour Jord,
La première propriété laisse penser qu'il s'agit d'une fonction affine croissante sur l'ensemble des réels.
Bon, la troisième, tout est dedans...
Et enfin, la deuxième laisse penser qu'il s'agit d'une fonction linéaire.
Donc je dirais que la fonction f qui associe x à x est l'ensemble des solutions :) (enfin j'en suis pas sûr)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Déc 2010, 12:51
par ffpower » 11 Déc 2010, 12:51
La premiere dirait plutot que f est linéaire, donc de la forme f(x)=ax ( et pas nécessairement croissante d'ailleurs ). Mais en fait c'est pas nécessairement vrai. Ya besoin de régularité supplémentaire pour conclure ( continuité, monotonie, ou autre ). C'est la condition 2 qui aidera à obtenir cette régularité. Quand à la 3eme condition, elle sert pas grand chose, à part à dire à la fin que a=1 ( mais bon, la condition 2 implique déjà que a=1 ou -1)
Sinon, ya quand même un petit prob dans l'énoncé de division éventuelle par 0..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 12:54
par Nightmare » 11 Déc 2010, 12:54
Salut à vous deux !
ffpower > Ca m'a l'air de bien marcher. Plutôt que de récupérer la monotonie, j'ai trouvé plus simple de montrer simplement que notre fonction était bornée (ajout : au voisinage de 0 ), et pour ça : [color="white"] suffit juste de voir que x+1/x est minorée par 2 puis f(x+1/x)=...[/color]
Aaaie > Malheureusement, toutes les fonctions affines ne vérifient pas la première propriété, et en plus, il n'y a pas qu'elles, même si en exhiber une non R-linéaire n'est pas "évident" (prendre une base de R sur Q)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Déc 2010, 12:58
par Doraki » 11 Déc 2010, 12:58
Attend, t'as montré que f(x) = x est une fonction bornée, ou j'ai mal lu ?
-
Anonyme
 par Anonyme » 11 Déc 2010, 12:59
par Anonyme » 11 Déc 2010, 12:59
Jord > Et encore, j'aurais du penser linéaire. Mais bon...
J'aurais bien pensé à la fonction partie entière, mais la propriété (f(x))^-1 = f(x^-1) empêchait que ça soit la fonction partie entière (parce que ça voudrait dire que pour tout x compris entre 0 et 1 ; f(x^-1) serait égal à plus l'infini ?) ; ou peut-être à la fonction x-E(x) mais ça marchait pas.
Donc bon, je ne vois pas de fonction non-affine respecter la première propriété... :D
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Déc 2010, 13:01
par Doraki » 11 Déc 2010, 13:01
Aaaie : ben c'est un peu dur à imaginer.
C'est bien plus facile d'imaginer une fonction de
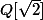
dans R, qui vérifie le 1, mais qui n'est pas affine.
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 11 Déc 2010, 13:01
par vincentroumezy » 11 Déc 2010, 13:01
Ou, je pense qu'il y'a deux applications solutions, f(x)=x et -x, pour tout x dans R* (je crois que j'ai un peu répété la meme chose).
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 13:02
par Nightmare » 11 Déc 2010, 13:02
Doraki a écrit:Attend, t'as montré que f(x) = x est une fonction bornée, ou j'ai mal lu ?
Au voisinage de 0 à ajouter évidemment :lol3:
-
Anonyme
 par Anonyme » 11 Déc 2010, 13:02
par Anonyme » 11 Déc 2010, 13:02
La fonction g : x |--> -x n'est pas solution car f(1) = 1 et ici g(1) = -1.
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 11 Déc 2010, 13:04
par vincentroumezy » 11 Déc 2010, 13:04
C'est juste. Je pense donc qu'il n'y a qu'une solution.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 13:13
par benekire2 » 11 Déc 2010, 13:13
Salut à tous ,
En effet, l'identité est la seule application vérifiant cela , f(x+y)=f(x)+f(y) implique que f est linéaire OU BIEN que f est une application tordue non continue et probablement dense dans R² (i.e en gros son graphe est ... le plan entier) et donc le must serait de retrouver la continuité. Un peu chaud ... et la croissance suffit très bien pour conclure ou alors le f(xy)=f(x)f(y) montre que f est un endomorphisme de R i.e l'identité. (c'est la même chose)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 13:15
par Nightmare » 11 Déc 2010, 13:15
A ce niveau,ie celui de la question, tout ce qui est dit est bien entendu... a démontrer :lol3:
-
Anonyme
 par Anonyme » 11 Déc 2010, 13:22
par Anonyme » 11 Déc 2010, 13:22
Je dirais que f' est constante ? Donc fonction linéaire, la seule qui admet les trois propriétés est f(x) = x. :)
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 11 Déc 2010, 13:23
par vincentroumezy » 11 Déc 2010, 13:23
C'est vrai que moi je peut te dire que telle fonction marche, mai pour démontrer que c'est la seule, alors là.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 13:25
par Nightmare » 11 Déc 2010, 13:25
Aaaie a écrit:Je dirais que f' est constante ? Donc fonction linéaire, la seule qui admet les trois propriétés est f(x) = x.

Le fond de l'idée n'est pas mauvais, mais, problème, je n'ai pas supposé f dérivable, même pas continue a priori ! Et il semble assez vain de prouver tel quel que c'est effectivement le cas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
telles que
?
