Conserve la somme et l'inverse
Olympiades mathématiques, énigmes et défis
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Déc 2010, 14:14
par ffpower » 11 Déc 2010, 14:14
Nightmare a écrit:La première est un indice pour la seconde :lol3:
Sinon, concernant la preuve via f(xy)=f(x)f(y) elle est correcte mais vraiment très longue si l'on doit tout redémontrer.
Je ne suis pas du genre à vanter les mérite de mes propre preuves (sauf pour ennuyer Ben) , mais pour le coup, montrer que f est nécessairement bornée au voisinage de 0 est vraiment beaucoup plus rapide
Pas d'accord, la preuve de f(xy)=f(x)f(y) fait une ligne ( ligne qui peut se raccourcir si on se contente de f(x²)=f(x)² ), tout comme ta preuve de f bornée au voisinage de 0 fait une ligne. Mais en suite, c'est plus long de conclure à partir de "f localement bornée" que de "f(x²)=f(x)²".
Tout ça pour dire : :fuck2: :langue2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 14:17
par Nightmare » 11 Déc 2010, 14:17
Ben faut quand même montrer que la croissance implique que c'est l'identité, et ça c'est au moins 1 ligne plus long que de le montrer avec la bornitude :D
Et nous sommes d'accord pour dire qu'1 ligne en moins, c'est beaucoup plus rapide non? ^^
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Déc 2010, 14:23
par Doraki » 11 Déc 2010, 14:23
Avec l'indic de nightmare, moi ça a plutôt donné ça :
si r est rationnel positif, pour tout y >= r, y s'écrit x/2r + 1/2rx, donc f(y) = f(x)/2r + 1/2rf(x) >= r
et pour tout 0 = 1/r donc 1/f(y) = f(1/y) >= 1/r donc 0 < f(y) <= r,
Donc les intervalles rationnels sont stables, donc f est continue et f = id

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 11 Déc 2010, 14:24
par Olympus » 11 Déc 2010, 14:24
Salut !
Aaaie a écrit:f(x+1) = f(x) + f(1) = f(x) + 1 donc f est croissante.
Euh non, revois ta définition de la croissance

Sinon, une indice, suppose que, pour un y quelconque,
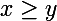
. Que peux-tu dire de
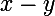
? Sers-toi ensuite de l'équation fonctionnelle et ce qui a déjà été démontré précédemment :
=f\left(x\right)f\left(y\right))
.
Petite question : je me demandais toujours si l'équation de Cauchy était résoluble sans invoquer l'argument de la densité de Q dans R, et donc sans l'hypothèse de continuité, et j'ai lu que oui, mais d'autres solutions s'ajoutent alors ( c'était quelque chose en rapport avec les bases de Hamel et l'axiome du choix ) . Ici, ça diffère, y a plus de contraintes que dans l'équation de Cauchy, et l'hypothèse de continuité n'est pas présente dans l'énoncé ( même si l'équation l'implique vu que la fonction solution est bien continue ) . Donc je me demandais si on ne pouvait pas s'en sortir ici sans la densité ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Déc 2010, 14:30
par Doraki » 11 Déc 2010, 14:30
Bah que Q est dense dans R c'est quasiment dans la définition de R.
Je vois pas comment tu comptes t'en passer.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Déc 2010, 14:31
par ffpower » 11 Déc 2010, 14:31
Avec la méthode de Doraki/moi, ça donne ça :
f(x²)=f(x+(1/(x-1)-1/x)^{-1})=f(x)+(1/(f(x)-1)-1/f(x))^{-1}=f(x)², donc x>y=>f(x)-f(y)=f(racine(x-y))²>0
Donc f est croissante, et de plus vaut l'identité sur les rationnels.
Donc les intervalles rationnels sont stables, donc f est continue et f = idPas évident de statuer, j'avoue

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 14:38
par benekire2 » 11 Déc 2010, 14:38
Olympus a écrit:Salut !
Euh non, revois ta définition de la croissance

Sinon, une indice, suppose que, pour un y quelconque,
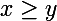
. Que peux-tu dire de
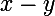
? Sers-toi ensuite de l'équation fonctionnelle et ce qui a déjà été démontré précédemment :
=f\left(x\right)f\left(y\right))
.
Petite question : je me demandais toujours si l'équation de Cauchy était résoluble sans invoquer l'argument de la densité de Q dans R, et donc sans l'hypothèse de continuité, et j'ai lu que oui, mais d'autres solutions s'ajoutent alors ( c'était quelque chose en rapport avec les bases de Hamel et l'axiome du choix ) . Ici, ça diffère, y a plus de contraintes que dans l'équation de Cauchy, et l'hypothèse de continuité n'est pas présente dans l'énoncé ( même si l'équation l'implique vu que la fonction solution est bien continue ) . Donc je me demandais si on ne pouvait pas s'en sortir ici sans la densité ?
J'ai posté la même "indic" il y a 10 minutes hélas il y a eu 20 messages depuis ... :we:
Salut Bouazza !
Pour répondre a ta question tu semble dire que continuité densité de Q dans R , sauf que la densité de Q dans R est un fait , et la continuité tu n'est certainement pas obligé de l'imposer à f ici !! Sinon que veut dire "imposer la densité de Q dans R a f " ?? Enfin, relis ça attentivement et tu verra pourquoi la question n'a pas trop de sens.
Bon, sinon, FF >> Oui , mais nightmare veut qu'on explicite pourquoi f est croissante pour tout b >0 pour tout a , f(a+b)=f(a)+f(b)>f(a) et puis après conclure par densité"en détail" , je tranche en faveur de nightmare

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Déc 2010, 14:41
par Doraki » 11 Déc 2010, 14:41
J'ajouterais que j'ai utilisé le TVI sur la fonction x -> x+1/x, ce qui complexifie mon histoire comparé à la preuve passant par f(x²)=f(x)².
Bon en fait, j'aurais pu dire 2rx+1/2rx = y <=> x = (y+-sqrt(y²-r²))/r
Et en fait dans les deux preuves on utilise crucialement que tout nombre positif a une racine carrée.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 14:42
par benekire2 » 11 Déc 2010, 14:42
Doraki a écrit:J'ajouterais que j'ai utilisé le TVI sur la fonction x -> x+1/x, ce qui complexifie mon histoire comparé à la preuve passant par f(x²)=f(x)².
Certes , mais je crois que nightmare préfère la preuve "moins longue" à la preuve "moins coûteuse" :ptdr:
( Je joue l'avocat du diable .. )
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 14:45
par benekire2 » 11 Déc 2010, 14:45
Nightmare >> Euh , en fait je vois pas trop pour l'histoire modulo n ( deuxième équation ) , je connais quasi rien en équations fonctionnelles , peut-tu m'aider ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 14:46
par Nightmare » 11 Déc 2010, 14:46
Bon, de manière équivalente, moi ça donnait :
[color="white"] |f(x+1/x)|=|f(x)+1/f(x)| minoré par 2 et x->x+1/x surjective sur {y, y >= 2} => |f| >=2 , et passage à l'inverse => |f| = f(x)=lim_n r(n)=x.[/color]
Bon je l'admets, c'est un peu plus long !
Edit : j'ai l'impression de mettre 2 fois plus de temps à taper un texte sans latex qu'avec...
Edit 2 : Dans ma preuve aussi, on utilise que tout nombre positif a une racine carrée ... (pour le même calcul)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Déc 2010, 14:48
par ffpower » 11 Déc 2010, 14:48
Je crois qu'on va arrêter pour la bataille de la preuve la plus courte :ptdr:
( A moins que Ben arrive avec une autre variante^^ )

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 11 Déc 2010, 14:49
par Olympus » 11 Déc 2010, 14:49
Doraki a écrit:Bah que Q est dense dans R c'est quasiment dans la définition de R.
Je vois pas comment tu comptes t'en passer.
Je pensais à une solution astucieuse qui n'utiliserait que des identités pas forcément évidentes ( comme la tienne, celle de ffpower ou celle d'Imod ), enfin, une preuve comme celles que nous avons présenté moi et ffpower dans le topic
http://www.maths-forum.com/deuxieme-test-marocain-2011-114070.php .
@Benekire : Euh non, je ne dis pas que "continuité densité de Q dans R", je me suis peut-être mal exprimé ( je crois que c'est dû à mon "donc sans l'hypothèse de continuité" ) . Je voulais juste savoir si on pouvait résoudre cette équation fonctionnelle sans utiliser l'argument de densité, car j'ai remarqué plusieurs implications dans les preuves proposées ici : ... => ... => multiplicité de f => monotonie de f => conclusion par la densité . Et peut-être que y a plus direct .
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 14:53
par benekire2 » 11 Déc 2010, 14:53
Olympus a écrit:Je pensais à une solution astucieuse qui n'utiliserait que des identités pas forcément évidentes ( comme la tienne, celle de ffpower ou celle d'Imod ), enfin, une preuve comme celle que nous avons présenté moi et ffpower dans le topic
http://www.maths-forum.com/deuxieme-test-marocain-2011-114070.php .
@Benekire : Euh non, je ne dis pas que "continuité densité de Q dans R", je me suis peut-être mal exprimé ( je crois que c'est dû à mon "donc sans l'hypothèse de continuité" ) . Je voulais juste savoir si on pouvait résoudre cette équation fonctionnelle sans utiliser l'argument de densité, car j'ai remarqué plusieurs implications dans les preuves proposées ici : ... => ... => multiplicité de f => monotonie de f => conclusion par la densité . Et peut-être que y a plus direct .
Hum , d'accord, en ces cas là , je ne sais pas , mais d'après moi c'est peu probable (en fait j'en sais rien) et j'aurais tendance a me demander si ça a une utilité face à une preuve aussi "simple" ( une fois qu'on connait obv .. )
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 14:56
par benekire2 » 11 Déc 2010, 14:56
ffpower a écrit:Je crois qu'on va arrêter pour la bataille de la preuve la plus courte :ptdr:
( A moins que Ben arrive avec une autre variante^^ )
Ne le provoque pas , j'ai peur qu'il vienne et nous humilie

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 15:01
par Nightmare » 11 Déc 2010, 15:01
benekire2 a écrit:Nightmare >> Euh , en fait je vois pas trop pour l'histoire modulo n ( deuxième équation ) , je connais quasi rien en équations fonctionnelles , peut-tu m'aider ?
Ici, c'est plus de l'algèbre.
Indice : Z, en tant que groupe additif est cyclique, Z=, pareil pour Z/nZ.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Déc 2010, 15:06
par ffpower » 11 Déc 2010, 15:06
Olympus : y a a peu près aucune chance. Quelque part, une solution "bidouillesque" comme dans le lien montre qu'on a la même conclusion dans à peu près n'importe quel espace ou on on peut faire nos opérations élémentaires ( un corps, donc, par exemple C ).Alors que l'équation f(x+y)=f(x)+f(y) et f(xy)=f(x)f(y) marche bien dans R grace à sa structure, mais peut donner beaucoup de solutions si on se place dans un autre corps ( rien que dans C, ya un nb indénombrables de solutions, non explicitement exprimables, bref c'est là cata^^ ). C'est pourquoi on est obligé d'utiliser des trucs "typiques à R" ici..
PS : si tu veux t'amuser avec une équation "bidouille only", je te conseille celle là :
http://www.maths-forum.com/equation-fonctionnelle-89066.phpJe l'avais fait avec Lapras par msn, et elle en a dans le ventre^^
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 15:23
par benekire2 » 11 Déc 2010, 15:23
Bon, donc Z et Z/nZ sont engendrés par un seul élément , ça c'est ok .
Maintenant je conjecture que les seules solutions de cette équation sont .. les fonctions linéaires , et j'espère que c'est ça. Maintenant , même si je vois que ton indic à l'air de vouloir "transposer" tout ça , je ne vois pas trop comment l'utiliser concrètement .
Désolé :triste:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Déc 2010, 16:01
par Nightmare » 11 Déc 2010, 16:01
Et c'est quoi les applications linéaires de Z->Z/nZ ? (Au passage, "linéaire", pour quelle structure? :lol3: )
Bon, sinon, la première chose qu'on fait dans R, c'est d'écrire que f(nx)=nf(x) pour tout entier n et réel x ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Déc 2010, 16:39
par benekire2 » 11 Déc 2010, 16:39
J'ai réfléchis et on va commencer a cherche f(0) , on a donc f(0)=2f(0) [n] i.e f(0)=0 [n] ensuite , f(1)=k mettons . f(2)=2k [n] ainsi par récurrence , pour tout n , f(n)=kn [n] Bon, normalement , on obtient , f(n)=kn [n] pour tout n dans Z , ainsi f : Z --> Z/nZ ; x --> f(1)x
C'est ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
