Conjecture - topologie générale
Olympiades mathématiques, énigmes et défis

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 24 Avr 2020, 10:46
par chombier » 24 Avr 2020, 10:46
Bonjour,
Soient
)
un espace topologique,
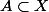
et
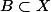
deux parties de X.
On suppose que
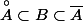
J'ai très envie de penser que
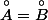
et que
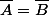
, cependant je n'arrive pas du tout à le démontrer, tellement pas que je doute, mais de là à trouver un contre exemple...
Si quelqu'un a une idée


-
GaBuZoMeu
- Habitué(e)
- Messages: 6141
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 24 Avr 2020, 11:09
par GaBuZoMeu » 24 Avr 2020, 11:09
Prends pour A la réunion de ]-1,0[, ]0,1[ et {2} et pour B, [-1,1].

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Avr 2020, 11:30
par Ben314 » 24 Avr 2020, 11:30
Sinon, pour donner un exemple éventuellement plus "parlant", si tu prend A=Q (dans R) alors toutes les parties B de

vérifient
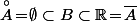
donc cette double inclusion ne donne pas la moindre information concernant
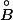
et
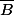
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 24 Avr 2020, 17:29
par chombier » 24 Avr 2020, 17:29
GaBuZoMeu a écrit:Prends pour A la réunion de ]-1,0[, ]0,1[ et {2} et pour B, [-1,1].
Top

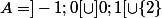
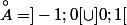
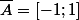
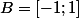
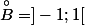
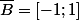
On a bien
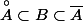
, pourtant
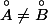
et que
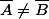
Au passage, ça m'entraine,
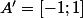
 = \{ 2 \})
(point isolés)
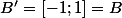
donc B est un fermé et n'a pas de points isolés
Ben314 a écrit:Sinon, pour donner un exemple éventuellement plus "parlant", si tu prend A=Q (dans R) alors toutes les parties B de

vérifient
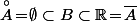
donc cette double inclusion ne donne pas la moindre information concernant
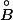
et
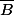
.
Merci Ben ! Capito !! Voila un exemple que je n'oublierais pas

-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Avr 2020, 18:13
par Imod » 24 Avr 2020, 18:13
C'est une excellente habitude que de se construire une série de contre-exemples barrières pour éviter de dire trop de bêtises .
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités


vérifient
donc cette double inclusion ne donne pas la moindre information concernant
et
.
