Conjecture "2^n"

[Mario2015]

n entier positif > 0

On definit une fonction S(k)

S(n)=2^n
S(n-1)= S(n) - (2^n-1)
S(n-2)= S(n-1)+(2^n-2)
S(n-3)=S(n-2)-(2^n-3)
....
S(0)=S(1)+ ou - (2^0)
le signe depend du depart on commence toujours par + et on alterne.

S(5)=2^5=32
S(4)=2^5-2^4=32-16=16
S(3)=16+2^3=24
S(2)=24-2^2=20
S(1)=20+2=22
S(0)=22-(2^0)=21

La conjecture "2^n" (je l`appellerai comme cela)

Pour tout n>0 il existe au moins un nombre k tel que n divise S(k)

Dans le cas de n=5

5 divise S(2)=20 donc k=2

Un contre-example?
Sinon une preuve?

Bref, le debat est ouvert

[Mario2015]

19 divise S(11)

17 divise S(10)

13 divise S(2)

etc....

Il devrait y avoir une certaine logique derriere ces chiffres.

[nodjim]

Que pour un modulo impair, ça se termine à 0, c'est normal: le -0 précède le +1 du départ. Que ce soit une boucle qui revienne à +1, c'est normal: il n'y a qu'un seul antécédent.
Que pour un modulo nombre pair, on n'a jamais 0, c'est normal: on revient sur le +1 par un -moitié du nombre pair.

Maintenant le constat que le 0 modulo impiar arrive au bout de n itérations max, ça reste à expliquer.

[Mario2015]

Que pour un modulo impair, ça se termine à 0, c'est normal: le -0 précède le +1 du départ. Que ce soit une boucle qui revienne à +1, c'est normal: il n'y a qu'un seul antécédent.
Que pour un modulo nombre pair, on n'a jamais 0, c'est normal: on revient sur le +1 par un -moitié du nombre pair.

Maintenant le constat que le 0 modulo impiar arrive au bout de n itérations max, ça reste à expliquer.

Honnetement, je n`ai pas compris ton commentaire.
Si tu peux etre plus explicite en donnant un exemple, peut-etre que je comprendrai mieux ta remarque.
Merci

[Mario2015]

Je donne l`exemple n=7

S(7)=128
S(6)=64
S(5)=96
S(4)=80
S(3)=88
S(2)=84
S(1)=86
S(0)=85

7 divise S(2)=84=7*12

Est-ce que c`est toujours vrai?
Y a-t-il un contre-exemple?
Pourquoi existe-t-il au moins un nombre k tel que n divise S(k)

Pour mieux comprendre ces suites lire :

https://oeis.org/A001045

Ce sont des suites connues. Les resultats listes sur OEIS donnent pour chaque n un S(0) correspondant. Moi, je detaille la suite de S(n) a S(0).

[zygomatique]

salut

soit n fixé

alors les termes avec 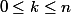sont la somme des termes d'une suite géométrique de raison -2



enfin un truc du genre

après c'est un problème de congruence : lorsque k parcourt 0, 1, 2 ..., n alors la division euclidienne de S(k) par n possède n + 1 restes donc l'un est nul ...

[Mario2015]

salut

soit n fixé

alors les termes avec sont la somme des termes d'une suite géométrique de raison -2



enfin un truc du genre

après c'est un problème de congruence : lorsque k parcourt 0, 1, 2 ..., n alors la division euclidienne de S(k) par n possède n + 1 restes donc l'un est nul ...

Merci pour cette tentative de preuve qui ne me convainc pas.
La sommation ne tient pas compte de l`alternance des signes + et -.
De plus S(k) peut etre formule autrement apres simplifications.
Quant a la partie congruence les restes modulo n sont cycliques.
Pourquoi l`un d`eux est forcement nul? Mystere!

[zygomatique]

La sommation ne tient pas compte de l`alternance des signes + et -

...

bien sur que si ....

et l'idée générale est là ....

il suffit/faut maintenant le faire avec rigueur ...

[Mario2015]

Un aveu que ta preuve manque de rigueur.

Ici pour n=17
en colonne 1 S(n) et en colonne 2 S(n) mod n

17 2
16 1
15 10
14 14
13 12
12 13
11 4
10 0
9 2
8 1
7 10
6 14
5 12
4 13
3 4
2 0
1 2
0 1

Je donne cela comme exemple pour les restes modulo n

En definitive je viens de trouver un moyen de generer "automatiquement" les S(n) pour tout n.
Une sorte de suite similaire a celle de Fibonnacci.
Je ne suis pas au bout du tunnel car ce que je cherche en fait cette suite particuliere ne m`avance pas ou peut-etre que peu.
Je m`attendais a une croissance rapide des cas ou n divise S(k) quand n est un nombre semi-premier impair. Plus n est grand plus le nombre des cas ou n divise S(k) croit de maniere "exponentielle" (j`exagere un peu).
Il y a un cycle lie a n ou les 0 se repetent.
Si j`arrive a comprendre ce cycle et a le prevoir mon probleme est resolu.

[zygomatique]

alors je ne comprends pas ...

d'après ton premier post et pour n = 17 ::



donc

[Mario2015]

alors je ne comprends pas ...

d'après ton premier post et pour n = 17 ::



donc

S(17)=2 mod 17
S(16)=1 mod 17
......
J`ai donne les restes mod 17

[zygomatique]

je t'ai demandé si ce que j'ai écrit est bien ce que tu considères ...


ensuite comme je l'ai dit s(k) est la somme des termes d'une suite géométrique .... que l'on peut donc calculer en fonction de k

enfin en considérant s(k) mod n pour k variant de 0 à n on arrive au résultat (avec éventuellement du travail bien sur) ....

ensuite évidemment ça dépendra de combien de diviseurs possède 0 dans Z/nZ (intégrité ou non)

RAP : dans Z/nZ un entier a 0 est dit diviseur de 0 s'il existe b 0 tel que ab = 0 (et donc b est aussi un diviseur de 0 ....

[Mario2015]

je t'ai demandé si ce que j'ai écrit est bien ce que tu considères ...


ensuite comme je l'ai dit s(k) est la somme des termes d'une suite géométrique .... que l'on peut donc calculer en fonction de k

enfin en considérant s(k) mod n pour k variant de 0 à n on arrive au résultat (avec éventuellement du travail bien sur) ....

ensuite évidemment ça dépendra de combien de diviseurs possède 0 dans Z/nZ (intégrité ou non)

RAP : dans Z/nZ un entier a 0 est dit diviseur de 0 s'il existe b 0 tel que ab = 0 (et donc b est aussi un diviseur de 0 ....

Ce que tu as ecrit est bien ce que je considere.
S(k) pour un n donne peut etre exprime bien plus simplement en se basant sur cette suite de Jacobsthal :

https://oeis.org/A001045

La suite est generee a la "Fibonnacci".

Prouver la conjecture 2^n revient a prouver que dans cette suite A(n) il y a toujours un element A(k) de la suite (k<n) que divise n.

[Mario2015]

Un type m`a fourni une preuve detaillee sur la conjecture.
Comme ce n`est pas ecrit en Latex j`ai du mal a dechiffrer ses formules.
Voir ici la preuve de "Cauchy" (c`est son pseudo) :

http://forums.xkcd.com/viewtopic.php?f=17&t=112380

[zygomatique]

et bien c'est exactement ce que je dis sans détailler ...

et il passe aussi par la somme d'une série géométrique !!!!

et congruence et décomposition de n en produit de facteur 2 et 3 (vu la valeur de s(k)) et du reste ....

[Mario2015]

En simplifiant S(n) on retrouve un moyen d`ecrire de maniere plus simple S(n)

S(n)=2^n
S(n-1)=(2^n-1)*(2-1)
S(n-2)=(2^n-2)*(4-2+1)
S(n-3)=(2^n-3)*(8-4+2-1)
etc....
On retrouve la sequence de Jacobsthal : 1,1,3,5,11,21,....
qui s`ecrit tres rapidement partant de 1,1
1*2+1=3
1*2+3=5
3*2+5=11
5*2+11=21
etc....
D`ou la forme generale de S(k)=(2^k)*C(i) ou C(i) est un element de la suite de Jacobsthal.

[Mario2015]

Cela etant dit, les S(k) pour les nombres premiers a partir d`un certain rang >3 ont une caracteristique COMMUNE.

S(2) = 0 mod n quand n est un nombre premier.

Laquelle?
Pourquoi?

[Mario2015]

Cette preuve me semble la plus elegante pour le moment

http://math.stackexchange.com/questions/1381819/how-come-n-always-divides-at-least-one-of-the-item-of-the-sequence

[Mario2015]

Meme avec a^n (a entier >=2) cela marche.

[Mario2015]

Test de primalite rapide.

Pour tout n il est facile de calculer S(n)=2^n
On suppose que n>10^3
Peut-on trouver facilement la valeur de S(2) moyennant une formule "ingenieuse" et calculable "rapdement" independamment de la taille de n?
Si tel est le cas on aurait le test de primalite le plus rapide.
Si n est premier S(2) mod n = 0
A verifier pour n entier impair > a une certaine valeur.