Salut,
Combien peut-on mettre, au maximum, de pierres sur un goban si on veut que 4 d'entre elles ne forment jamais un rectangle à cotés parallèles au bord du goban ?
Un goban (<-image) est constitué de 19 segments horizontaux et verticaux et les pierres se placent sur des intersections de segments.
Et sur une grille de 1981 x 1981 ?
Un carré sans rectangles
14 messages
- Page 1 sur 1
Re: Un carré sans rectangles
pas trop le temps, dommage j'aime bien.
Donc juste pour animer le fil:
je suis à 70 pour le moment.
autre idée de décomposition mais cela ne semble pas améliorer le schmilblick.
pas vu s'il marchait mais il serait alors à 80 le suivant...pas encore optimisé mais cela vient?
ok pour ma grille 80 semble-t-il qui marcherait à 78?
Donc juste pour animer le fil:
je suis à 70 pour le moment.
autre idée de décomposition mais cela ne semble pas améliorer le schmilblick.
pas vu s'il marchait mais il serait alors à 80 le suivant...pas encore optimisé mais cela vient?
ok pour ma grille 80 semble-t-il qui marcherait à 78?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Un carré sans rectangles
J'en ai 83, réparties sur 6 diagonales.
Je ne crois pas qu'il y ait la possibilité de trouver ces diagonales analytiquement.
Je ne crois pas qu'il y ait la possibilité de trouver ces diagonales analytiquement.
Re: Un carré sans rectangles
J'ai essayé de trouver une analogie avec des graphes orientés où la matrice d'adjacence serait la grille, et qu'il ne faudrait pas de "relation cyclique symétrique de taille 4" pour de pas avoir de rectangle sur la matrice, ce qui m'a permis d'estimer la croissance en fonction du côté de la grille n, ce qui donne O(n^(3/2)) pièces.
Je cherche à présent une relation de récurrence ....
EDIT:
Je suis d'accord avec nodgim pour le 83 qui suit la relation de croissance ceil(19^(3/2)) = 83
Je cherche à présent une relation de récurrence ....
EDIT:
Je suis d'accord avec nodgim pour le 83 qui suit la relation de croissance ceil(19^(3/2)) = 83
Re: Un carré sans rectangles
En fait, je viens de voir que "le vrai" optimum, ben je l'ai pas....
J'ai uniquement un majorant explicite (i.e. plus précis qu'un simple O(???)) qui semble ne pas être trop mauvais.
Sauf que, même dans le cas de 1981, ben contrairement à ce que je pensait au début, j'ai bien l'impression que mon majorant n'est pas optimum...
Pour 19, le majorant que j'ai est 90 et clairement, on ne peut pas mettre 90 pierres sur le goban.
Je sais pas si on peut faire un algo. raisonnable (en temps) pour déterminer le max (un truc de sûr, c'est que si on y va bourrin pour l'algo., ça risque pas de donner quoi que ce soit avant la nuit des temps...)
Bref, on va dire que le but est juste d'obtenir un majorant explicite et "pas trop mauvais".
J'ai uniquement un majorant explicite (i.e. plus précis qu'un simple O(???)) qui semble ne pas être trop mauvais.
Sauf que, même dans le cas de 1981, ben contrairement à ce que je pensait au début, j'ai bien l'impression que mon majorant n'est pas optimum...
Pour 19, le majorant que j'ai est 90 et clairement, on ne peut pas mettre 90 pierres sur le goban.
Je sais pas si on peut faire un algo. raisonnable (en temps) pour déterminer le max (un truc de sûr, c'est que si on y va bourrin pour l'algo., ça risque pas de donner quoi que ce soit avant la nuit des temps...)
Bref, on va dire que le but est juste d'obtenir un majorant explicite et "pas trop mauvais".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Un carré sans rectangles
90 marche pour un 20*20.
Je pensais qu'on pouvait s'en sortir avec cette méthode:
1) Les pierres sont groupées en lignes obliques ( 45°) parallèles dont l'écart doit être unique.
2) Le premier écart disponible permet de placer une ligne de pierres la plus près possible de la diagonale ( assurer un max de pierres), à savoir, dans un repère orthonormé, le plus près de 0 en négatif ou positif.
Le problème est un peu plus compliqué que le simple écart: il nous permettrait de placer la ligne "-19" sauf que ça ne marche pas. Le principe de l'écart unique est bon, mais le numéro de ligne à attribuer ne correspond à dernière ligne + écart disponible.
A remarquer tout de même : les lignes que j'ai choisies de placer en négatif sont : 0,2,8,20, soit la série des k(k-1) = 1*2 + 2*3 + 3*4...mais je ne peux pas le prouver. Les lignes placées en positif : 0 , 1, 5, 15, 31 ne sont pas bien parlantes.
Il est possible de mettre tout ça dans une machine avec un algorithme propre.
Je pensais qu'on pouvait s'en sortir avec cette méthode:
1) Les pierres sont groupées en lignes obliques ( 45°) parallèles dont l'écart doit être unique.
2) Le premier écart disponible permet de placer une ligne de pierres la plus près possible de la diagonale ( assurer un max de pierres), à savoir, dans un repère orthonormé, le plus près de 0 en négatif ou positif.
Le problème est un peu plus compliqué que le simple écart: il nous permettrait de placer la ligne "-19" sauf que ça ne marche pas. Le principe de l'écart unique est bon, mais le numéro de ligne à attribuer ne correspond à dernière ligne + écart disponible.
A remarquer tout de même : les lignes que j'ai choisies de placer en négatif sont : 0,2,8,20, soit la série des k(k-1) = 1*2 + 2*3 + 3*4...mais je ne peux pas le prouver. Les lignes placées en positif : 0 , 1, 5, 15, 31 ne sont pas bien parlantes.
Il est possible de mettre tout ça dans une machine avec un algorithme propre.
Re: Un carré sans rectangles
...........................….encore faux!
Modifié en dernier par beagle le 08 Nov 2018, 08:59, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Un carré sans rectangles
"Je pensais qu'on pouvait s'en sortir avec cette méthode:
1) Les pierres sont groupées en lignes obliques ( 45°) parallèles dont l'écart doit être unique.
2) Le premier écart disponible permet de placer une ligne de pierres la plus près possible de la diagonale ( assurer un max de pierres), à savoir, dans un repère orthonormé, le plus près de 0 en négatif ou positif. "
Et ça marche, à condition de ne pas oublier d'écarts !
Donc, soit un intervalle [-C; +C]. Le problème revient à y trouver "n" entiers relatifs tels que tous les écarts absolus entre 2 quelconques d'entre eux sont distincts.
Le nombre de pierres qu'on peut poser sur le jeu vaut : C*n - sInI.........avec sInI: somme des valeurs absolues des n valeurs. Implicitement, cela conduit à trouver les valeurs les plus proches de 0.
Les 1ères valeurs : 0, 1, -2, 5, -8, 15, -20, 31, -42, 59, -80, 105......
Au delà, si un programmeur veut bien s'y intéresser......
NB: Certains écarts ne sont pas utilisables ( le plus petit est 11). Le majorant pourrait être calculé sur la base de l'utilisation de tous les écarts.
1) Les pierres sont groupées en lignes obliques ( 45°) parallèles dont l'écart doit être unique.
2) Le premier écart disponible permet de placer une ligne de pierres la plus près possible de la diagonale ( assurer un max de pierres), à savoir, dans un repère orthonormé, le plus près de 0 en négatif ou positif. "
Et ça marche, à condition de ne pas oublier d'écarts !
Donc, soit un intervalle [-C; +C]. Le problème revient à y trouver "n" entiers relatifs tels que tous les écarts absolus entre 2 quelconques d'entre eux sont distincts.
Le nombre de pierres qu'on peut poser sur le jeu vaut : C*n - sInI.........avec sInI: somme des valeurs absolues des n valeurs. Implicitement, cela conduit à trouver les valeurs les plus proches de 0.
Les 1ères valeurs : 0, 1, -2, 5, -8, 15, -20, 31, -42, 59, -80, 105......
Au delà, si un programmeur veut bien s'y intéresser......
NB: Certains écarts ne sont pas utilisables ( le plus petit est 11). Le majorant pourrait être calculé sur la base de l'utilisation de tous les écarts.
Re: Un carré sans rectangles
Salut nodgim,
oui c'est tout à fait cela.
Je n'avais pas bien compris la description avec tes mots.
Mais oui maintenant que je comprends tes phrases c'est cela bien sur à quoi je jouais ces derniers jours, avec encore quelques réglages et plantages dans mes superpositions...
oui c'est tout à fait cela.
Je n'avais pas bien compris la description avec tes mots.
Mais oui maintenant que je comprends tes phrases c'est cela bien sur à quoi je jouais ces derniers jours, avec encore quelques réglages et plantages dans mes superpositions...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Un carré sans rectangles
OK.
J'avais écrit que certains écarts n'étaient pas disponibles, or curieusement, s'ils ne sont pas disponibles pour un nombre, ils peuvent très bien l'être pour un nombre plus grand. Tel est le cas de 11 et 19. Mais de bien d'autres aussi.
Les 1ères valeurs trouvées :
0, 1, -2, 5, -8, 15, -20, 31, -42, 59, -80, 105, -91, 124, -136, 174, -188, 236......
On observera -91 trouvé APRES 105.
J'avais écrit que certains écarts n'étaient pas disponibles, or curieusement, s'ils ne sont pas disponibles pour un nombre, ils peuvent très bien l'être pour un nombre plus grand. Tel est le cas de 11 et 19. Mais de bien d'autres aussi.
Les 1ères valeurs trouvées :
0, 1, -2, 5, -8, 15, -20, 31, -42, 59, -80, 105, -91, 124, -136, 174, -188, 236......
On observera -91 trouvé APRES 105.
Re: Un carré sans rectangles
Salut nodgim,
comment on justifie qu'il faut 6 semidiagos minimisées qs plutôt que 7 diagos d'une série moins performante?
Puisque le nombre de placement sera
6x19 moins les valeurs absolues de tes écarts
pourquoi 7x19 - somme des valeurs absolues d'écarts moins optimisés est effectivement inférieur?
comment on justifie qu'il faut 6 semidiagos minimisées qs plutôt que 7 diagos d'une série moins performante?
Puisque le nombre de placement sera
6x19 moins les valeurs absolues de tes écarts
pourquoi 7x19 - somme des valeurs absolues d'écarts moins optimisés est effectivement inférieur?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Un carré sans rectangles
Bonjour à tous ,
je n'ai pas cherché le problème , je fais juste quelques remarques en l'air ( sans prétention ) .
1°) On peut généraliser à une grille rectangulaire .
2°) En retournant la question , on cherche le nombre de nœuds à occuper pour empêcher la construction d'un rectangle .
3°) Le nombre de rectangles de sommet donné est le même pour chaque sommet .
4°) Un rectangle est parfaitement défini par une de ses diagonales .
Est-on en théorie des graphes ou en combinatoire ? J'adore ces problèmes où on ne sait plus où l'on habite , je regrette simplement d'avoir de moins en moins de temps à y consacrer
Merci Ben pour ce joli problème .
Imod
je n'ai pas cherché le problème , je fais juste quelques remarques en l'air ( sans prétention ) .
1°) On peut généraliser à une grille rectangulaire .
2°) En retournant la question , on cherche le nombre de nœuds à occuper pour empêcher la construction d'un rectangle .
3°) Le nombre de rectangles de sommet donné est le même pour chaque sommet .
4°) Un rectangle est parfaitement défini par une de ses diagonales .
Est-on en théorie des graphes ou en combinatoire ? J'adore ces problèmes où on ne sait plus où l'on habite , je regrette simplement d'avoir de moins en moins de temps à y consacrer

Merci Ben pour ce joli problème .
Imod
Re: Un carré sans rectangles
Vu que ça s'enterre un peu, je peut donner le majorant que je connais :
Si on est sur un rectangle de ligne par
ligne par  colonnes, alors, s'il y a
colonnes, alors, s'il y a  pierres sur la première ligne, ça signifie qu'il y a
pierres sur la première ligne, ça signifie qu'il y a ) couples de pierres sur cette ligne. Idem pour les autres lignes avec
couples de pierres sur cette ligne. Idem pour les autres lignes avec 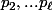
Et le "théorème des tiroirs" nous dit que, si la somme de ces nombres de couples dépasse strictement le nombre total de couple faisable sur une ligne, c'est à dire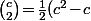) , ça signifie qu'il y a deux lignes distinctes portant le même couple de pierres, c'est à dire qu'il y a un rectangle de 4 pierres.
, ça signifie qu'il y a deux lignes distinctes portant le même couple de pierres, c'est à dire qu'il y a un rectangle de 4 pierres.
Donc si on veut qu'il n'y ait pas de rectangles, il faut obligatoirement que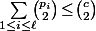 c'est à dire que
c'est à dire que 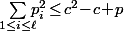 avec
avec 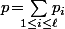 qui est le nombre total de pierre.
qui est le nombre total de pierre.
 donc }\dfrac{p^2}{\ell}\!\leq\!\sum_{1\leq i\leq \ell}\!\!\! p_i^2\text{ et on doit avoir })
}\,\big)\ \Big[=\frac{\ell}{2}\big(1\!+\!\sqrt{4\ell\!-\!3}\,\big)\sim\ell^{3/2}\text{ si }c\!=\!\ell\,\Big])
Sauf que, même dans le cas où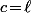 et où
et où 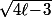 est entier (ce qui est le cas de
est entier (ce qui est le cas de 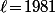 ), ce majorant n'est pas optimum : dans ce cas, il faudrait exactement le même nombre de pierres par lignes (pour que Cauchy-Schwarz soit une égalité) et il faudrait aussi que tout les couples de pierres apparaissent exactement une fois sur une des lignes, mais ça coince...
), ce majorant n'est pas optimum : dans ce cas, il faudrait exactement le même nombre de pierres par lignes (pour que Cauchy-Schwarz soit une égalité) et il faudrait aussi que tout les couples de pierres apparaissent exactement une fois sur une des lignes, mais ça coince...
Si on est sur un rectangle de
Et le "théorème des tiroirs" nous dit que, si la somme de ces nombres de couples dépasse strictement le nombre total de couple faisable sur une ligne, c'est à dire
Donc si on veut qu'il n'y ait pas de rectangles, il faut obligatoirement que
Sauf que, même dans le cas où
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Un carré sans rectangles
Salut Ben314,
perso j'ai encore un peu joué avec ce truc, mais je suis limité.
Sur le plan des démonstrations j'aurais au mieux essayé de montrer pour le 19x19 , 5 par lignes sur toutes les lignes, ben on n'aurait pas le nombre de C(19,5) avec de zero à un seul de commun sur 19 lignes.Déjà tres péniblement ou meme pas possible par moi.Et cela ne prouvait pas que 6 et 4 sur deux lignes plutôt que tout à 5.Bref pas les moyens maths de démontrer.
Heureusement ce genre de problème permet de jouer avec des crayons de couleur en remplissant des grilles.
Mais là comme nodgim les structures qui permettent d'avancer vont jusqu' à 83 maxi.
Dès que l'on s'affranchit des règles qui mènent à 83, ben on se supprime plutôt des degrés de liberté plutôt qu'on en retrouve. Donc perso ton majorant à 90 pour le 19x19, si on ne peut pas l'atteindre cela pourrait aller jusqu'à 89, ben perso j'aimerais bien voir la tete d'une grille à 84 ou 85 juste pour voir...
perso j'ai encore un peu joué avec ce truc, mais je suis limité.
Sur le plan des démonstrations j'aurais au mieux essayé de montrer pour le 19x19 , 5 par lignes sur toutes les lignes, ben on n'aurait pas le nombre de C(19,5) avec de zero à un seul de commun sur 19 lignes.Déjà tres péniblement ou meme pas possible par moi.Et cela ne prouvait pas que 6 et 4 sur deux lignes plutôt que tout à 5.Bref pas les moyens maths de démontrer.
Heureusement ce genre de problème permet de jouer avec des crayons de couleur en remplissant des grilles.
Mais là comme nodgim les structures qui permettent d'avancer vont jusqu' à 83 maxi.
Dès que l'on s'affranchit des règles qui mènent à 83, ben on se supprime plutôt des degrés de liberté plutôt qu'on en retrouve. Donc perso ton majorant à 90 pour le 19x19, si on ne peut pas l'atteindre cela pourrait aller jusqu'à 89, ben perso j'aimerais bien voir la tete d'une grille à 84 ou 85 juste pour voir...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
