Calcul de probabilité
30 messages
- Page 1 sur 2 - 1, 2
Calcul de probabilité
Bonjour,
je me suis posé un problème que je ne suis pas certain de résoudre correctement.
En considérant une séquence donnée de huit chiffres, je souhaite calculer la probabilité que celle-ci n'apparaisse jamais dans une séquence aléatoire d'un milliard de chiffres.
J'ai pensé dans un premier temps à faire (99 999 999 / 100 000 000)^1 000 000 000 (désolé mais pour une raison que j'ignore l'insertion de formules latex ne marche pas) mais je ne suis pas pleinement convaincu. Qu'en pensez vous ?
je me suis posé un problème que je ne suis pas certain de résoudre correctement.
En considérant une séquence donnée de huit chiffres, je souhaite calculer la probabilité que celle-ci n'apparaisse jamais dans une séquence aléatoire d'un milliard de chiffres.
J'ai pensé dans un premier temps à faire (99 999 999 / 100 000 000)^1 000 000 000 (désolé mais pour une raison que j'ignore l'insertion de formules latex ne marche pas) mais je ne suis pas pleinement convaincu. Qu'en pensez vous ?
Re: Calcul de probabilité
C'est plus compliqué que cela.
On voit des variantes de cette question parfois, sous la forme : un singe tape au hasard sur une machine à écrire, quelle est la probabilité qu'il obtienne abracadabra ?
Ca peut t'aider à retrouver des discussions sur ce thème.
Une des difficultés, c'est que la réponse n'est pas la même selon que ta séquence de 8 chiffres est 12345678 par exemple, ou 88888888.
Si la chaîne recherchée est 88888888, si elle apparaît une fois, la probabilité qu'elle apparaisse 2 fois est forte (il suffit que le 9ème chiffre soit encore un 8 )
Si la chaîne cherchée est 12341234, on est un peu dans la même situation que 88888888 mais pas tout à fait.
Si la chaîne cherchée est 12345123, on est un peu dans la même situation, mais on s'éloigne progressivement.
Si la chaîne cherchée est 12345612, on est un peu dans la même situation, mais on s'éloigne progressivement.
Si la chaîne cherchée est 12345671 (ou 12222221, ou 12344321 etc c'est pareil), on est un peu dans la même situation, mais on s'éloigne progressivement.
Et si la chaîne cherchée est 12345678, rien de commun entre le début et la fin, on est à l'autre extrémité du spectre.
Dans le cas abracadabra, on cherche une chaîne de longueur 11, avec les 4 caractères du début répétés à la fin...
Tout ce que je raconte là c'était valable pour la question : Quelle est l'espérance du rang de la première apparition de telle chaîne ?
A priori, ça reste valable pour l'exercice que tu proposes.
On voit des variantes de cette question parfois, sous la forme : un singe tape au hasard sur une machine à écrire, quelle est la probabilité qu'il obtienne abracadabra ?
Ca peut t'aider à retrouver des discussions sur ce thème.
Une des difficultés, c'est que la réponse n'est pas la même selon que ta séquence de 8 chiffres est 12345678 par exemple, ou 88888888.
Si la chaîne recherchée est 88888888, si elle apparaît une fois, la probabilité qu'elle apparaisse 2 fois est forte (il suffit que le 9ème chiffre soit encore un 8 )
Si la chaîne cherchée est 12341234, on est un peu dans la même situation que 88888888 mais pas tout à fait.
Si la chaîne cherchée est 12345123, on est un peu dans la même situation, mais on s'éloigne progressivement.
Si la chaîne cherchée est 12345612, on est un peu dans la même situation, mais on s'éloigne progressivement.
Si la chaîne cherchée est 12345671 (ou 12222221, ou 12344321 etc c'est pareil), on est un peu dans la même situation, mais on s'éloigne progressivement.
Et si la chaîne cherchée est 12345678, rien de commun entre le début et la fin, on est à l'autre extrémité du spectre.
Dans le cas abracadabra, on cherche une chaîne de longueur 11, avec les 4 caractères du début répétés à la fin...
Tout ce que je raconte là c'était valable pour la question : Quelle est l'espérance du rang de la première apparition de telle chaîne ?
A priori, ça reste valable pour l'exercice que tu proposes.
Re: Calcul de probabilité
Bonsoir,
Il est vrai que la probabilité d'apparition d'une chaîne dépend de la chaîne en question.
Simplifions les choses, et comparons dans une suite de 20 tirages à pile ou face les probabilités d'apparition de PPF et celles de PPP. La première a un peu plus de 97% de chance de se produire, la deuxième un peu moins de 79%. Comment expliquer cette nette différence ?
Supposons qu'au cours de la suite de tirages on ait déjà obtenu PP. Dans le cas où on veut PPP, si on rate et qu'on tire un F, on repart à zéro pour obtenir les trois P de suite. Tandis que dans le cas où on veut PPF, si on rate et qu'on tire un P, on a toujours PP dans les deux derniers tirages, on ne repart pas à zéro et on a une chance sur deux d'avoir PPF au coup d'après.
Il est vrai que la probabilité d'apparition d'une chaîne dépend de la chaîne en question.
Simplifions les choses, et comparons dans une suite de 20 tirages à pile ou face les probabilités d'apparition de PPF et celles de PPP. La première a un peu plus de 97% de chance de se produire, la deuxième un peu moins de 79%. Comment expliquer cette nette différence ?
Supposons qu'au cours de la suite de tirages on ait déjà obtenu PP. Dans le cas où on veut PPP, si on rate et qu'on tire un F, on repart à zéro pour obtenir les trois P de suite. Tandis que dans le cas où on veut PPF, si on rate et qu'on tire un P, on a toujours PP dans les deux derniers tirages, on ne repart pas à zéro et on a une chance sur deux d'avoir PPF au coup d'après.
Re: Calcul de probabilité
Les chances varient de 10/1 à 1/4032 selon qu'il s'agisse respectivement d'une chaîne de 8 caractères identiques ou de 8 caractères différents.
Le rapport de 40320 correspond à une difficulté d'ordonnancement des 8 chiffres dans la chaîne (8!=1x2x3x4x5x6x7x8) qui disparaît pour une chaîne de 8 chiffres identiques.
Pour le reste 10^8 correspond à la probabilité de trouver les 8 chiffres de la chaîne dans le désordre, et 10^9 (10^9 - 7 pour être exact) le nombre de tentatives pour y parvenir. (Nombre de décalages d'un chiffre dans la chaîne d'1milliard de chiffres pour ).
Vous en pensez quoi ?
Je pense ne pas être très loin du compte.
Le rapport de 40320 correspond à une difficulté d'ordonnancement des 8 chiffres dans la chaîne (8!=1x2x3x4x5x6x7x8) qui disparaît pour une chaîne de 8 chiffres identiques.
Pour le reste 10^8 correspond à la probabilité de trouver les 8 chiffres de la chaîne dans le désordre, et 10^9 (10^9 - 7 pour être exact) le nombre de tentatives pour y parvenir. (Nombre de décalages d'un chiffre dans la chaîne d'1milliard de chiffres pour ).
Vous en pensez quoi ?
Je pense ne pas être très loin du compte.
Re: Calcul de probabilité
Bonjour,
Je ne comprends pas ce que tu calcules exactement. La probabilité de trouver une chaîne de 8 chiffres donnée dans une suite d'un milliard de chiffres ?
Je ne comprends pas ce que tu calcules exactement. La probabilité de trouver une chaîne de 8 chiffres donnée dans une suite d'un milliard de chiffres ?
Re: Calcul de probabilité
Oui, c'est ce que j'ai calculé: la probabilité de trouver exactement cette chaîne de 8 chiffres dans une chaîne d'1milliard de chiffres.
On doit pouvoir en déduire la probabilité de ne pas la trouver, non?
On doit pouvoir en déduire la probabilité de ne pas la trouver, non?
Re: Calcul de probabilité
la probabilité de trouver exactement cette chaîne de 8 chiffres dans une chaîne d'1milliard de chiffres.
Et tu dis que ça vaut quoi ??? Désolé, mais je ne te trouve vraiment pas clair, et pour ce que je crois comprendre de ce que tu écris, c'est faux - mais peut-être je comprends mal. Formule donc les choses clairement.
Re: Calcul de probabilité
Tu dis que la probabilité vaut 10 quand ... ...
Dans mes cours, une probabilité ne dépasse jamais 1.
Dans mes cours, une probabilité ne dépasse jamais 1.
Re: Calcul de probabilité
Bonsoir,
Effectivement j'ai pas forcément été très clair et j'ai aussi commis une erreur.
Je reprends:
Dans ma réflexion j'ai fait une comparaison avec le tirage de l'euromillions
Un pots "numéros" avec 50 boules numérotées de 1 à 50 et un pot "étoiles" avec 12 boules numérotées de 1 à 12
Sur ma grille de 50 numéros et 12 étoiles je coche 5 numéros et 2 étoiles.
Lors du tirage on retire 5 boules du pot "numéros" et 2 boules du pot "étoiles"
Les chances que ce tirage corresponde avec ma grille sont de:
1 chance sur 50*49*48*47*46*12*11 = 33 561 158 400
(Il s'agit ici de la probabilité de trouver la combinaison dans l'ordre exact ou j'ai coché les numéros car dans le désordre les chances sont de 1/139 838 160)
Dans notre problème, la chaine à trouver correspond à ma grille d'euromillions, à ceci près qu'elle est composée de 8 colonnes de chiffres numérotés de 0 à 9 et j'ai coché un chiffre dans chaque colonne.
Pour le tirage au sort, j'ai 8 pots de 10 boules numérotées de 0 à 9.
Je retire une boule de chaque pot, j'ai donc:
1 chance sur 10*10*10*10*10*10*10*10 = 10^8 de trouver les 8 chiffres.
Voici le début et la fin d'une chaine aléatoire d'1 milliard de chiffres:
4514004150354219458....534515040524053420534
Nous commençons par le début:
1 - 4514004150354219458....534515040524053420534
puis ensuite...
2 - 4514004150354219458....534515040524053420534
et ainsi de suite...
3 - 4514004150354219458....534515040524053420534
4 - 4514004150354219458....534515040524053420534
5 - 4514004150354219458....534515040524053420534
6 - 4514004150354219458....534515040524053420534
et pour finir ...
999 999 992 - 4514004150354219458....534515040524053420534
999 999 993 - 4514004150354219458....534515040524053420534
On a donc 999 999 993 tentatives avec à chaque fois une probabilité de 1/10^8 (1/100 000 000)
J'applique 999 999 993 / 100 000 000 = 9,99999993.
Cela signifie pour moi que statistiquement dans un très grand nombre de chaines d'1 milliard de chiffres on trouve en moyenne 10 exemplaires d'une même chaine de 8 chiffres.
Est-ce que c'est plus clair?
Donc pour la formule en fonction de la longueur de la chaine (c) et de la longueur de la sous-chaine (s) on aurait:
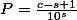
Effectivement j'ai pas forcément été très clair et j'ai aussi commis une erreur.
Je reprends:
Dans ma réflexion j'ai fait une comparaison avec le tirage de l'euromillions
Un pots "numéros" avec 50 boules numérotées de 1 à 50 et un pot "étoiles" avec 12 boules numérotées de 1 à 12
Sur ma grille de 50 numéros et 12 étoiles je coche 5 numéros et 2 étoiles.
Lors du tirage on retire 5 boules du pot "numéros" et 2 boules du pot "étoiles"
Les chances que ce tirage corresponde avec ma grille sont de:
1 chance sur 50*49*48*47*46*12*11 = 33 561 158 400
(Il s'agit ici de la probabilité de trouver la combinaison dans l'ordre exact ou j'ai coché les numéros car dans le désordre les chances sont de 1/139 838 160)
Dans notre problème, la chaine à trouver correspond à ma grille d'euromillions, à ceci près qu'elle est composée de 8 colonnes de chiffres numérotés de 0 à 9 et j'ai coché un chiffre dans chaque colonne.
Pour le tirage au sort, j'ai 8 pots de 10 boules numérotées de 0 à 9.
Je retire une boule de chaque pot, j'ai donc:
1 chance sur 10*10*10*10*10*10*10*10 = 10^8 de trouver les 8 chiffres.
Voici le début et la fin d'une chaine aléatoire d'1 milliard de chiffres:
4514004150354219458....534515040524053420534
Nous commençons par le début:
1 - 4514004150354219458....534515040524053420534
puis ensuite...
2 - 4514004150354219458....534515040524053420534
et ainsi de suite...
3 - 4514004150354219458....534515040524053420534
4 - 4514004150354219458....534515040524053420534
5 - 4514004150354219458....534515040524053420534
6 - 4514004150354219458....534515040524053420534
et pour finir ...
999 999 992 - 4514004150354219458....534515040524053420534
999 999 993 - 4514004150354219458....534515040524053420534
On a donc 999 999 993 tentatives avec à chaque fois une probabilité de 1/10^8 (1/100 000 000)
J'applique 999 999 993 / 100 000 000 = 9,99999993.
Cela signifie pour moi que statistiquement dans un très grand nombre de chaines d'1 milliard de chiffres on trouve en moyenne 10 exemplaires d'une même chaine de 8 chiffres.
Est-ce que c'est plus clair?
Donc pour la formule en fonction de la longueur de la chaine (c) et de la longueur de la sous-chaine (s) on aurait:
Re: Calcul de probabilité
Tu réponds à une question différente de celle posée.
Ton calcul semble correct, il convient pour la question que tu te poses.
La chaîne 12345678 apparaît combien de fois ?
Si on tire 123456789012345678901234567890 , tu vas dire que la chaîne 12345678 est apparue 3 fois ... et ça compense les tirages où elle n'apparaît pas du tout.
Mais la question initiale était de savoir si la chaîne 12345678 apparaissait ou pas :
Dans 123456789012345678901234567890, 12345678 apparaît. Que ce soit 1 fois, ou 3 fois,on s'en moque.
Et là, ta formule ne marche plus.
Comme expliqué, il y a certaines séquences qui sont propices pour se répéter, et d'autres beaucoup moins.
Si on cherche la chaîne 99999999, elle apparaît ni plus souvent ni moins souvent que la chaîne 12345678 selon ton calcul. Mais les tirages où elle apparaît sont moins nombreux que pour 12345678.
Parce que, quand 99999999 apparaît, souvent (10% des cas), il apparaît au moins une 2ème fois.
Ton calcul semble correct, il convient pour la question que tu te poses.
La chaîne 12345678 apparaît combien de fois ?
Si on tire 123456789012345678901234567890 , tu vas dire que la chaîne 12345678 est apparue 3 fois ... et ça compense les tirages où elle n'apparaît pas du tout.
Mais la question initiale était de savoir si la chaîne 12345678 apparaissait ou pas :
Dans 123456789012345678901234567890, 12345678 apparaît. Que ce soit 1 fois, ou 3 fois,on s'en moque.
Et là, ta formule ne marche plus.
Comme expliqué, il y a certaines séquences qui sont propices pour se répéter, et d'autres beaucoup moins.
Si on cherche la chaîne 99999999, elle apparaît ni plus souvent ni moins souvent que la chaîne 12345678 selon ton calcul. Mais les tirages où elle apparaît sont moins nombreux que pour 12345678.
Parce que, quand 99999999 apparaît, souvent (10% des cas), il apparaît au moins une 2ème fois.
Re: Calcul de probabilité
La où je ne te rejoins pas, c'est que les statistiques se moquent bien de la composition de chaque chaîne, elles s'appliquent équitablement à toutes les chaînes de la même façon.
Ce que tu avances n'est basé que sur des impressions, mais as-tu seulement passé en revue une chaîne d'1milliard de chiffres ?
Si tu veux constater de tes yeux, tu peux appliquer la formule en gardant le même rapport de 10 avec par exemple une chaîne de 3 chiffres dans une autre de 10 000, tu constateras que 123, 678, 666 ou 284 se répètent environ 10 fois chacune en moyenne sur un grand nombre de série.
Ce que tu avances n'est basé que sur des impressions, mais as-tu seulement passé en revue une chaîne d'1milliard de chiffres ?
Si tu veux constater de tes yeux, tu peux appliquer la formule en gardant le même rapport de 10 avec par exemple une chaîne de 3 chiffres dans une autre de 10 000, tu constateras que 123, 678, 666 ou 284 se répètent environ 10 fois chacune en moyenne sur un grand nombre de série.
Re: Calcul de probabilité
Tu as fait des expériences.
Tu constates que si on cherche une chaîne de 3 caractères dans une chaîne de 10000, cette chaîne se retrouve en moyenne une dizaine de fois. Avec peu de différences pour des chaînes comme 666 ou comme 284.
Soit.
Très bien. Ca répond à la question que tu te poses.
La question de Ben474 était différente. Et je ne vois aucun élément de réponse à la question de Ben474 dans tes messages.
Tu constates que si on cherche une chaîne de 3 caractères dans une chaîne de 10000, cette chaîne se retrouve en moyenne une dizaine de fois. Avec peu de différences pour des chaînes comme 666 ou comme 284.
Soit.
Très bien. Ca répond à la question que tu te poses.
La question de Ben474 était différente. Et je ne vois aucun élément de réponse à la question de Ben474 dans tes messages.
Re: Calcul de probabilité
les statistiques se moquent bien de la composition de chaque chaîne
C'est faux. Dois-je répéter ce que j'ai déjà écrit et que tu n'as pas lu, semble-t-il ?
comparons dans une suite de 20 tirages à pile ou face les probabilités d'apparition de PPF et celles de PPP. La première a un peu plus de 97% de chance de se produire, la deuxième un peu moins de 79%.
Re: Calcul de probabilité
Bonjour Nikogil,
Ce qui ne va pas dans ton explication, c'est que tu considères que les tentatives sont indépendantes or ce n'est pas le cas puisqu'il y a plusieurs tirages en commun entre chaque tentative.
Ce qui est vrai, c'est de dire que la probabilité d'avoir une certaine chaine de 8 caractères dans 8 tirages successifs est la même quelque soit la chaine de caractère.
Ce qui est faux, c'est de dire sachant qu'on a échoué ou réussi à avoir une certaine chaine de 8 caractères dans les 8 premiers tirages alors cela ne change pas la probabilité d'avoir la chaine de 8 caractères entre le 2ème et le 9ème tirage.
Exemple : on veut avoir la chaine 00 ou avoir la chaine 01 avec des tirages équiprobables entre 0 et 1
on a autant de chance d'avoir les 8 chaines suivantes
000 => gagné perdu
001 => gagné gagné
010 => perdu gagné
100 => gagné perdu
011 => perdu gagné
101 => perdu gagné
110 => perdu perdu
111 => perdu perdu
On a bel et bien sur les 2 premiers tirages P(00x)=P(01x)=P(10x)=P(11x)=1/4 et sur les 2 derniers tirages P(y00)=P(y01)=P(y10)=P(y11)=1/4
Donc la probabilité d'avoir 00 quelque part est P(00x)+P(y00)-P(000) = 1/4 + 1/4 - 1/8 = 3/8 comme on peut le voir précédemment
La probabilité d'avoir 01 quelque part est P(01x)+P(y01) = 1/4+1/4=4/8 comme on peut le voir précédemment aussi.
Ce qui ne va pas dans ton explication, c'est que tu considères que les tentatives sont indépendantes or ce n'est pas le cas puisqu'il y a plusieurs tirages en commun entre chaque tentative.
Ce qui est vrai, c'est de dire que la probabilité d'avoir une certaine chaine de 8 caractères dans 8 tirages successifs est la même quelque soit la chaine de caractère.
Ce qui est faux, c'est de dire sachant qu'on a échoué ou réussi à avoir une certaine chaine de 8 caractères dans les 8 premiers tirages alors cela ne change pas la probabilité d'avoir la chaine de 8 caractères entre le 2ème et le 9ème tirage.
Exemple : on veut avoir la chaine 00 ou avoir la chaine 01 avec des tirages équiprobables entre 0 et 1
on a autant de chance d'avoir les 8 chaines suivantes
000 => gagné perdu
001 => gagné gagné
010 => perdu gagné
100 => gagné perdu
011 => perdu gagné
101 => perdu gagné
110 => perdu perdu
111 => perdu perdu
On a bel et bien sur les 2 premiers tirages P(00x)=P(01x)=P(10x)=P(11x)=1/4 et sur les 2 derniers tirages P(y00)=P(y01)=P(y10)=P(y11)=1/4
Donc la probabilité d'avoir 00 quelque part est P(00x)+P(y00)-P(000) = 1/4 + 1/4 - 1/8 = 3/8 comme on peut le voir précédemment
La probabilité d'avoir 01 quelque part est P(01x)+P(y01) = 1/4+1/4=4/8 comme on peut le voir précédemment aussi.
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Calcul de probabilité
Merci,
Je commençai à désespérer. Enfin des arguments fondés et exploitables pour avancer sur le sujet.
Ton explication est très claire, mais sans trop réfléchir (il est 2h20) j'identifie deux axes de recherche:
- Quelle est la tendance observable des probabilités que tu as démontré quand on augmente la taille de la chaine C (4, 5, 6, 7, etc) sans augmenter la taille du motif M recherché. Vas-ton vers un équilibre au fur est à mesure que le rapport C/M tends vers l'infini?
- Ne peut-on pas borner la probabilité en découpant la chaine C en x morceaux de taille M. Car pour chacun de ces morceaux distincts on a la même probabilité?
Je commençai à désespérer. Enfin des arguments fondés et exploitables pour avancer sur le sujet.
Ton explication est très claire, mais sans trop réfléchir (il est 2h20) j'identifie deux axes de recherche:
- Quelle est la tendance observable des probabilités que tu as démontré quand on augmente la taille de la chaine C (4, 5, 6, 7, etc) sans augmenter la taille du motif M recherché. Vas-ton vers un équilibre au fur est à mesure que le rapport C/M tends vers l'infini?
- Ne peut-on pas borner la probabilité en découpant la chaine C en x morceaux de taille M. Car pour chacun de ces morceaux distincts on a la même probabilité?
Re: Calcul de probabilité
On cherche un motif de longueur M dans une chaîne de longueur C avec des caractères choisis dans un alphabet qui contient D caractères.
On considère qu'il y a succès dès que le motif apparaît au moins une fois.
La probabilité d'avoir un succès dépend de D et des longueurs M et C, et elle dépend aussi du motif cherché (Pour une longueur C fixée, strictement supérieure à 3, on aura moins de succès pour 666 que pour 864)
Si on augmente la longueur de la chaîne C, quel est l'impact ? Plus on augmente la longueur C, plus l'écart entre les 2 motifs diminue.
Si on cherche un motif de longueur 3 dans des chaînes de longueur 100000, avec un alphabet composé de 10 caractères, on a une probabilité très très forte de le trouver au moins une fois dans chacune des chaînes, et expérimentalement, on ne verra pas la différence. Tel motif ou tel autre, on aura quasiment 100% de succès pour les 2 cas.
Le tout premier message de GBZM donnait des résultats forts : pour certains choix de (D,M,C), on a 79% de succès avec un motif, et 97% de succès avec un autre motif.
On considère qu'il y a succès dès que le motif apparaît au moins une fois.
La probabilité d'avoir un succès dépend de D et des longueurs M et C, et elle dépend aussi du motif cherché (Pour une longueur C fixée, strictement supérieure à 3, on aura moins de succès pour 666 que pour 864)
Si on augmente la longueur de la chaîne C, quel est l'impact ? Plus on augmente la longueur C, plus l'écart entre les 2 motifs diminue.
Si on cherche un motif de longueur 3 dans des chaînes de longueur 100000, avec un alphabet composé de 10 caractères, on a une probabilité très très forte de le trouver au moins une fois dans chacune des chaînes, et expérimentalement, on ne verra pas la différence. Tel motif ou tel autre, on aura quasiment 100% de succès pour les 2 cas.
Le tout premier message de GBZM donnait des résultats forts : pour certains choix de (D,M,C), on a 79% de succès avec un motif, et 97% de succès avec un autre motif.
Re: Calcul de probabilité
Les explications de Lyceen95 ou GaBuZoMeu sont très bien et il savent tout comme moi comment calculer la probabilité exacte pour n'importe quelle séquence de caractère donc pas besoin d'encadrer par contre besoin de savoir laquelle.
Si tu as compris, on va essayer de compliquer et on travaille maintenant avec 3 chiffres équiprobables {1,2,3} à chaque tirage
-la probabilité d'avoir la séquence "123" en
d'avoir la séquence "123" en  tirages
tirages
si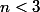 alors
alors 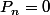 puisqu'on n'a même pas assez de tirages
puisqu'on n'a même pas assez de tirages
si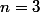 alors
alors 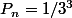 pour les raisons que tu connais
pour les raisons que tu connais
si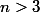 alors soit on a la séquence dans les
alors soit on a la séquence dans les  premiers tirages (proba
premiers tirages (proba 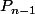 ), soit on va devoir attendre les 3 derniers tirages pour l'obtenir (proba
), soit on va devoir attendre les 3 derniers tirages pour l'obtenir (proba 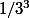 ) mais avant on ne l'avait pas (proba
) mais avant on ne l'avait pas (proba 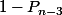 )
)
Donc au final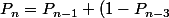/3^3)
-la probabilité d'avoir la séquence "111" en
d'avoir la séquence "111" en  tirages
tirages
si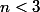 alors
alors 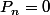 puisqu'on n'a même pas assez de tirages
puisqu'on n'a même pas assez de tirages
si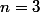 alors
alors 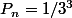 pour les raisons que tu connais
pour les raisons que tu connais
si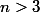 alors soit on a la séquence dans les
alors soit on a la séquence dans les  premiers tirages (proba
premiers tirages (proba 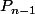 ), soit on va devoir attendre les 3 derniers tirages pour l'obtenir (proba
), soit on va devoir attendre les 3 derniers tirages pour l'obtenir (proba 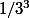 ) mais avant on ne l'avait pas comme précédemment.
) mais avant on ne l'avait pas comme précédemment.
Donc ici en plus, il faut que le tirage précédent les 3 derniers ne soit pas 1 (proba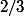 ) sinon on aurait la séquence à l'avant-dernier tirage au lieu du dernier tirage.
) sinon on aurait la séquence à l'avant-dernier tirage au lieu du dernier tirage.
Donc au final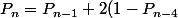/3^4)
Il y a aussi les chaines de Markov mais il faut avoir des bases en algèbre linéaire ou du moins de calcul matriciel pour comprendre
Avec 1 tirages, la probabilité d'avoir 123 est de 0.00% et celle de 111 est de 0.00%
Avec 2 tirages, la probabilité d'avoir 123 est de 0.00% et celle de 111 est de 0.00%
Avec 3 tirages, la probabilité d'avoir 123 est de 3.70% et celle de 111 est de 3.70%
Avec 4 tirages, la probabilité d'avoir 123 est de 7.41% et celle de 111 est de 6.17%
Avec 5 tirages, la probabilité d'avoir 123 est de 11.11% et celle de 111 est de 8.64%
Avec 6 tirages, la probabilité d'avoir 123 est de 14.68% et celle de 111 est de 11.11%
Avec 7 tirages, la probabilité d'avoir 123 est de 18.11% et celle de 111 est de 13.49%
Avec 8 tirages, la probabilité d'avoir 123 est de 21.40% et celle de 111 est de 15.81%
Avec 9 tirages, la probabilité d'avoir 123 est de 24.56% et celle de 111 est de 18.06%
Avec 10 tirages, la probabilité d'avoir 123 est de 27.59% et celle de 111 est de 20.26%
Avec 11 tirages, la probabilité d'avoir 123 est de 30.50% et celle de 111 est de 22.39%
Avec 12 tirages, la probabilité d'avoir 123 est de 33.30% et celle de 111 est de 24.47%
Avec 13 tirages, la probabilité d'avoir 123 est de 35.98% et celle de 111 est de 26.49%
Avec 14 tirages, la probabilité d'avoir 123 est de 38.55% et celle de 111 est de 28.46%
Avec 15 tirages, la probabilité d'avoir 123 est de 41.02% et celle de 111 est de 30.38%
Avec 16 tirages, la probabilité d'avoir 123 est de 43.39% et celle de 111 est de 32.24%
Avec 17 tirages, la probabilité d'avoir 123 est de 45.67% et celle de 111 est de 34.06%
Avec 18 tirages, la probabilité d'avoir 123 est de 47.85% et celle de 111 est de 35.83%
Avec 19 tirages, la probabilité d'avoir 123 est de 49.95% et celle de 111 est de 37.54%
Avec 20 tirages, la probabilité d'avoir 123 est de 51.96% et celle de 111 est de 39.22%
Avec 21 tirages, la probabilité d'avoir 123 est de 53.89% et celle de 111 est de 40.85%
Avec 22 tirages, la probabilité d'avoir 123 est de 55.75% et celle de 111 est de 42.43%
Avec 23 tirages, la probabilité d'avoir 123 est de 57.53% et celle de 111 est de 43.97%
Avec 24 tirages, la probabilité d'avoir 123 est de 59.24% et celle de 111 est de 45.47%
Avec 25 tirages, la probabilité d'avoir 123 est de 60.87% et celle de 111 est de 46.93%
Avec 26 tirages, la probabilité d'avoir 123 est de 62.45% et celle de 111 est de 48.36%
Avec 27 tirages, la probabilité d'avoir 123 est de 63.96% et celle de 111 est de 49.74%
Avec 28 tirages, la probabilité d'avoir 123 est de 65.41% et celle de 111 est de 51.09%
Avec 29 tirages, la probabilité d'avoir 123 est de 66.80% et celle de 111 est de 52.40%
Avec 30 tirages, la probabilité d'avoir 123 est de 68.13% et celle de 111 est de 53.67%
Avec 31 tirages, la probabilité d'avoir 123 est de 69.41% et celle de 111 est de 54.91%
Avec 32 tirages, la probabilité d'avoir 123 est de 70.64% et celle de 111 est de 56.12%
Avec 33 tirages, la probabilité d'avoir 123 est de 71.82% et celle de 111 est de 57.29%
Avec 34 tirages, la probabilité d'avoir 123 est de 72.96% et celle de 111 est de 58.44%
Avec 35 tirages, la probabilité d'avoir 123 est de 74.04% et celle de 111 est de 59.55%
Avec 36 tirages, la probabilité d'avoir 123 est de 75.09% et celle de 111 est de 60.64%
Avec 37 tirages, la probabilité d'avoir 123 est de 76.09% et celle de 111 est de 61.69%
Avec 38 tirages, la probabilité d'avoir 123 est de 77.05% et celle de 111 est de 62.72%
Avec 39 tirages, la probabilité d'avoir 123 est de 77.97% et celle de 111 est de 63.71%
Avec 40 tirages, la probabilité d'avoir 123 est de 78.86% et celle de 111 est de 64.69%
Avec 41 tirages, la probabilité d'avoir 123 est de 79.71% et celle de 111 est de 65.63%
Avec 42 tirages, la probabilité d'avoir 123 est de 80.52% et celle de 111 est de 66.55%
Avec 43 tirages, la probabilité d'avoir 123 est de 81.31% et celle de 111 est de 67.45%
Avec 44 tirages, la probabilité d'avoir 123 est de 82.06% et celle de 111 est de 68.32%
Avec 45 tirages, la probabilité d'avoir 123 est de 82.78% et celle de 111 est de 69.17%
Avec 46 tirages, la probabilité d'avoir 123 est de 83.47% et celle de 111 est de 70.00%
Avec 47 tirages, la probabilité d'avoir 123 est de 84.14% et celle de 111 est de 70.80%
Avec 48 tirages, la probabilité d'avoir 123 est de 84.77% et celle de 111 est de 71.58%
Avec 49 tirages, la probabilité d'avoir 123 est de 85.39% et celle de 111 est de 72.34%
Avec 50 tirages, la probabilité d'avoir 123 est de 85.97% et celle de 111 est de 73.08%
Si tu as compris, on va essayer de compliquer et on travaille maintenant avec 3 chiffres équiprobables {1,2,3} à chaque tirage
-la probabilité
si
si
si
Donc au final
-la probabilité
si
si
si
Donc ici en plus, il faut que le tirage précédent les 3 derniers ne soit pas 1 (proba
Donc au final
Il y a aussi les chaines de Markov mais il faut avoir des bases en algèbre linéaire ou du moins de calcul matriciel pour comprendre
Avec 1 tirages, la probabilité d'avoir 123 est de 0.00% et celle de 111 est de 0.00%
Avec 2 tirages, la probabilité d'avoir 123 est de 0.00% et celle de 111 est de 0.00%
Avec 3 tirages, la probabilité d'avoir 123 est de 3.70% et celle de 111 est de 3.70%
Avec 4 tirages, la probabilité d'avoir 123 est de 7.41% et celle de 111 est de 6.17%
Avec 5 tirages, la probabilité d'avoir 123 est de 11.11% et celle de 111 est de 8.64%
Avec 6 tirages, la probabilité d'avoir 123 est de 14.68% et celle de 111 est de 11.11%
Avec 7 tirages, la probabilité d'avoir 123 est de 18.11% et celle de 111 est de 13.49%
Avec 8 tirages, la probabilité d'avoir 123 est de 21.40% et celle de 111 est de 15.81%
Avec 9 tirages, la probabilité d'avoir 123 est de 24.56% et celle de 111 est de 18.06%
Avec 10 tirages, la probabilité d'avoir 123 est de 27.59% et celle de 111 est de 20.26%
Avec 11 tirages, la probabilité d'avoir 123 est de 30.50% et celle de 111 est de 22.39%
Avec 12 tirages, la probabilité d'avoir 123 est de 33.30% et celle de 111 est de 24.47%
Avec 13 tirages, la probabilité d'avoir 123 est de 35.98% et celle de 111 est de 26.49%
Avec 14 tirages, la probabilité d'avoir 123 est de 38.55% et celle de 111 est de 28.46%
Avec 15 tirages, la probabilité d'avoir 123 est de 41.02% et celle de 111 est de 30.38%
Avec 16 tirages, la probabilité d'avoir 123 est de 43.39% et celle de 111 est de 32.24%
Avec 17 tirages, la probabilité d'avoir 123 est de 45.67% et celle de 111 est de 34.06%
Avec 18 tirages, la probabilité d'avoir 123 est de 47.85% et celle de 111 est de 35.83%
Avec 19 tirages, la probabilité d'avoir 123 est de 49.95% et celle de 111 est de 37.54%
Avec 20 tirages, la probabilité d'avoir 123 est de 51.96% et celle de 111 est de 39.22%
Avec 21 tirages, la probabilité d'avoir 123 est de 53.89% et celle de 111 est de 40.85%
Avec 22 tirages, la probabilité d'avoir 123 est de 55.75% et celle de 111 est de 42.43%
Avec 23 tirages, la probabilité d'avoir 123 est de 57.53% et celle de 111 est de 43.97%
Avec 24 tirages, la probabilité d'avoir 123 est de 59.24% et celle de 111 est de 45.47%
Avec 25 tirages, la probabilité d'avoir 123 est de 60.87% et celle de 111 est de 46.93%
Avec 26 tirages, la probabilité d'avoir 123 est de 62.45% et celle de 111 est de 48.36%
Avec 27 tirages, la probabilité d'avoir 123 est de 63.96% et celle de 111 est de 49.74%
Avec 28 tirages, la probabilité d'avoir 123 est de 65.41% et celle de 111 est de 51.09%
Avec 29 tirages, la probabilité d'avoir 123 est de 66.80% et celle de 111 est de 52.40%
Avec 30 tirages, la probabilité d'avoir 123 est de 68.13% et celle de 111 est de 53.67%
Avec 31 tirages, la probabilité d'avoir 123 est de 69.41% et celle de 111 est de 54.91%
Avec 32 tirages, la probabilité d'avoir 123 est de 70.64% et celle de 111 est de 56.12%
Avec 33 tirages, la probabilité d'avoir 123 est de 71.82% et celle de 111 est de 57.29%
Avec 34 tirages, la probabilité d'avoir 123 est de 72.96% et celle de 111 est de 58.44%
Avec 35 tirages, la probabilité d'avoir 123 est de 74.04% et celle de 111 est de 59.55%
Avec 36 tirages, la probabilité d'avoir 123 est de 75.09% et celle de 111 est de 60.64%
Avec 37 tirages, la probabilité d'avoir 123 est de 76.09% et celle de 111 est de 61.69%
Avec 38 tirages, la probabilité d'avoir 123 est de 77.05% et celle de 111 est de 62.72%
Avec 39 tirages, la probabilité d'avoir 123 est de 77.97% et celle de 111 est de 63.71%
Avec 40 tirages, la probabilité d'avoir 123 est de 78.86% et celle de 111 est de 64.69%
Avec 41 tirages, la probabilité d'avoir 123 est de 79.71% et celle de 111 est de 65.63%
Avec 42 tirages, la probabilité d'avoir 123 est de 80.52% et celle de 111 est de 66.55%
Avec 43 tirages, la probabilité d'avoir 123 est de 81.31% et celle de 111 est de 67.45%
Avec 44 tirages, la probabilité d'avoir 123 est de 82.06% et celle de 111 est de 68.32%
Avec 45 tirages, la probabilité d'avoir 123 est de 82.78% et celle de 111 est de 69.17%
Avec 46 tirages, la probabilité d'avoir 123 est de 83.47% et celle de 111 est de 70.00%
Avec 47 tirages, la probabilité d'avoir 123 est de 84.14% et celle de 111 est de 70.80%
Avec 48 tirages, la probabilité d'avoir 123 est de 84.77% et celle de 111 est de 71.58%
Avec 49 tirages, la probabilité d'avoir 123 est de 85.39% et celle de 111 est de 72.34%
Avec 50 tirages, la probabilité d'avoir 123 est de 85.97% et celle de 111 est de 73.08%
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Calcul de probabilité
Kekia évoque les chaînes de Markov, allons-y en python :
Probabilité d'obtenir 11111111 dans une chaîne de 100000000 chiffres : 59.34%
Probabilité d'obtenir 12345678 dans une chaîne de 100000000 chiffres : 63.21%
- Code: Tout sélectionner
import numpy as np
P=np.zeros((9,9))
P[-1,-1]=1.
for i in range(8) :
P[i,0]=.9
P[i,i+1]=.1
Q=np.zeros((9,9))
Q[-1,-1]=1.
Q[0,0]=.9 ; Q[0,1]=.1
for i in range(1,8) :
Q[i,0]=.8
Q[i,1]=.1
Q[i,i+1]=.1
n=10**8
p=np.linalg.matrix_power(P,n)[0,-1]
print("Probabilité d'obtenir 11111111 dans une chaîne de {} chiffres : {:.2%}"\
.format(n,p))
q=np.linalg.matrix_power(Q,n)[0,-1]
print("Probabilité d'obtenir 12345678 dans une chaîne de {} chiffres : {:.2%}"\
.format(n,q))
Probabilité d'obtenir 11111111 dans une chaîne de 100000000 chiffres : 59.34%
Probabilité d'obtenir 12345678 dans une chaîne de 100000000 chiffres : 63.21%
Re: Calcul de probabilité
En poussant un peu plus loin :
Probabilité d'obtenir 111111111 dans une chaîne de 1000000000 chiffres : 59.34%
Probabilité d'obtenir 123456789 dans une chaîne de 1000000000 chiffres : 63.21%
Remarquable stabilité (mais quand on va plus loin dans les décimales, ça diffère un tout petit peu).
En tout cas, confirmation du fait que la question "Quelle chaîne cherche-t-on" a son importance.
Probabilité d'obtenir 111111111 dans une chaîne de 1000000000 chiffres : 59.34%
Probabilité d'obtenir 123456789 dans une chaîne de 1000000000 chiffres : 63.21%
Remarquable stabilité (mais quand on va plus loin dans les décimales, ça diffère un tout petit peu).
En tout cas, confirmation du fait que la question "Quelle chaîne cherche-t-on" a son importance.
Re: Calcul de probabilité
Je sais bien que tu passes par les chaines de Markov, je ne voulais pas te gâcher ce plaisir 
Amusant résultat en tout cas mais à la réflexion je ne suis pas vraiment surprise vu la formule de récurrence,
Toujours dans la configuration où on a 10 chiffres équiprobables à chaque tirage.
En orange la probabilité d'avoir la séquence où il y a k chiffres distincts en fonction du nombre de tirages
En bleu la probabilité d'avoir la séquence où le même chiffre se répète k fois en fonction du nombre de tirages

Du coup, à ton avis Nikogil, la probabilité d'avoir une séquence précise de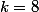 chiffres dans
chiffres dans 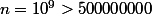 tirages, tu penses qu'elle vaut combien ?
tirages, tu penses qu'elle vaut combien ?
Amusant résultat en tout cas mais à la réflexion je ne suis pas vraiment surprise vu la formule de récurrence,
Toujours dans la configuration où on a 10 chiffres équiprobables à chaque tirage.
En orange la probabilité d'avoir la séquence où il y a k chiffres distincts en fonction du nombre de tirages
En bleu la probabilité d'avoir la séquence où le même chiffre se répète k fois en fonction du nombre de tirages

- Code: Tout sélectionner
import matplotlib.pyplot as plt
def dessin(n,k):
x=[]
ymax=[]
ymin=[]
for i in range (k):
x.append(i)
ymax.append(0)
ymin.append(0)
x.append(k)
ymax.append(1/10**k)
ymin.append(1/10**k)
for i in range (k+1,n):
x.append(i)
ymax.append(ymax[i-1]+(1-ymax[i-k])/10**k)
ymin.append(ymin[i-1]+9*(1-ymin[i-k-1])/10**(k+1))
plt.plot(x, ymin)
plt.plot(x, ymax)
plt.show()
Du coup, à ton avis Nikogil, la probabilité d'avoir une séquence précise de
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
