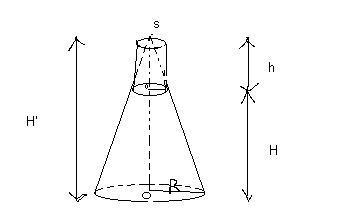
Une carafe en verre est représentée par le schéma ci-dessus.Elle se compose d'un tron de cône surmonté d'un cylindre.Le tronc de cône est obtenu en coupant un cône du sommet S de hauteur H'=H+h par un plan parallèle à sa base qui est un disque de centre O et de rayon R =7. On donne OO' = H = 21. De plus, le disque de centre O' a pour rayon r = 2. Le cylindre a pour base le dique de centre O'et de rayon r = 2 etpour hauteur SO' = h.
1- Calculer h.
7h=2(h+21)
5h=42
h=8.4
ou th.Thalès
2-Calculer la valeur exacte (en fonction de pi) du volume V1 du cône de sommet S et de hauteur H'.
V1= 7 X pi X 29.4 /3
=480,2 pi cm3
3- Calculer la valeur exacte (en fontion de pi) du volume V2 du cône de sommet S et de hauteur h.
2 X 2 X pi X 8,4 /3
= 11,2 pi cm3
4-En déduire la valeur exacte du volume V' (en fonction de pi) du tronc de cône.
480,2 pi - 11,2pi = 469 pi cm3
5-Calculer la valeur exacte du volume V'' (en fonction de pi) du cylindre.
2[ X 2 X pi X 8,4 = 33,6 pi cm3 = 168/5 pi
6-En déduire la mesure exacte du volume V (en fonction de pi) de la carafe
469 pi + 33,6 =502,6 pi cm3
7-Sachant que le volume du verre représente 10% du volume récédemment calculé,montrer que le volume exact maximum de liquide que peut contenir cette carafe est 452,34 pi cm3
8-On verse le contenu de cette carafe dans une autre carafe cylindrique de base un disque de rayon intérieur 7 cm et de hauteur 21cm.Quelle est la hauteur atteinte par le niveau d'eau ?
Je ne crois pas que les réponses soient fausses mais j'ai pas du tout compris les 2 dernières.
Merci encore !
