Geometrie dans l'espace ( shpère etc..)

[almagathe]

Aie confiance en toi un peu. Tu sais plein de trucs mais il faut t'en convaincre.

C'est presque ça, a²+a² c'est le carré de la diagonale (a²+b²=c² rappelle toi) donc la diagonale mesure

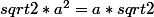
Tu me suis?

Hum..d'accord !

[Peacekeeper]

Hum..d'accord !

Maintenant, considère le triangle rectangle formé par une arrête, une diagonale de FACE et une diagonale de CUBE, tu le vois? Il traverse le cube en diagonale.

[almagathe]

Maintenant, considère le triangle rectangle formé par une arrête, une diagonale de FACE et une diagonale de CUBE, tu le vois? Il traverse le cube en diagonale.

heum..oui je vois !

[Peacekeeper]

heum..oui je vois !

Peux-tu écrire le théorème de Pythagore dans ce triangle? Sachant que l'arrête fait a, la diagonale de FACE fait et la diagonale du CUBE fait 10?

[almagathe]

Peux-tu écrire le théorème de Pythagore dans ce triangle? Sachant que l'arrête fait a, la diagonale de FACE fait et la diagonale du CUBE fait 10?

a² = (a x racine de 2)² + 10²
a² = ( ca fait combien au carré ? ) + 100

[Peacekeeper]

a² = (a x racine de 2)² + 10²
a² = ( ca fait combien au carré ? ) + 100

Attention, n'oublie pas où est l'hypoténuse. L'angle droit est entre l'arrête et la diagonale de face, donc l'hypoténuse est la diagonale du cube.

[almagathe]

Attention, n'oublie pas où est l'hypoténuse. L'angle droit est entre l'arrête et la diagonale de face, donc l'hypoténuse est la diagonale du cube.

10² = a² + ( a x racine carré de 2 )²
100 = a² + comment on calcule ça ?

[Peacekeeper]

10² = a² + ( a x racine carré de 2 )²
100 = a² + comment on calcule ça ?

Voilà.

C'est simple, ça fait

Tu vois?

[almagathe]

Voilà.

C'est simple, ça fait

Tu vois?

ah ok !

100 = a² +2a²
100 = a² + 4a²
100 = et là ca fait..?

[almagathe]

ah ok !

100 = a² +2a²
100 = a² + 4a²
100 = et là ca fait..?

Bon je vais arreter pour ce soir ! je n'arrive plus a reflechir..ni a comprendre
Merci beaucoup, au revoir !

[Peacekeeper]

ah ok !

100 = a² +2a²
100 = a² + 4a²
100 = et là ca fait..?

Heu, pourquoi 4a²? Tu as juste 100=a²+2a²=3a²

[Peacekeeper]

Bon je vais arreter pour ce soir ! je n'arrive plus a reflechir..ni a comprendre
Merci beaucoup, au revoir !

D'accord, bonne soirée.

[almagathe]

Heu, pourquoi 4a²? Tu as juste 100=a²+2a²=3a²

et donc quelle est la réponse finale alors ?... Pour connaitre l'arrête du cube

[Peacekeeper]

et donc quelle est la réponse finale alors ?... Pour connaitre l'arrête du cube

3a²=100 donc a²=100/3 donc donc

[mouette 22]

le problème du carré inscrit dans une sphère est entièrement traité si tu le demandes à google !
dessin clair et explication lumineuse .

[almagathe]

3a²=100 donc a²=100/3 donc donc

Hum..D'accord je comprend un peu mieux !
Mais sans vous déranger est ce que vous pourriez me recapitulez les calculs qu'il faut ecrire precisemment parce qu'avec nos nombreux messages je suis un peu perdue... :hum:
Qu'est ce que je dois ecrire exactement dans ma copie ?..
Merci beaucoup !!!!

[Peacekeeper]

Hum..D'accord je comprend un peu mieux !
Mais sans vous déranger est ce que vous pourriez me recapitulez les calculs qu'il faut ecrire precisemment parce qu'avec nos nombreux messages je suis un peu perdue... :hum:
Qu'est ce que je dois ecrire exactement dans ma copie ?..
Merci beaucoup !!!!

On cherche l'arrête du petit cube, on l'appelle a.
Appliquons le théorème de Pythagore au triangle ABC (nomme-le comme tu veux, c'est le triangle constitué par 2 arrêtes et une diagonale de face). a²+a²=b² (en appelant b la longueur de la diagonale de face), donc

Appliquons maintenant le théorème de Pythagore au triangle ABD (l'autre triangle rectangle, celui constitué d'une arrête, d'une diagonale de face et d'une diagonale du cube):
donc soit donc donc

[globule rouge]

On cherche l'arrête du petit cube, on l'appelle a.
Appliquons le théorème de Pythagore au triangle ABC (nomme-le comme tu veux, c'est le triangle constitué par 2 arrêtes et une diagonale de face). a²+a²=b² (en appelant b la longueur de la diagonale de face), donc

Appliquons maintenant le théorème de Pythagore au triangle ABD (l'autre triangle rectangle, celui constitué d'une arrête, d'une diagonale de face et d'une diagonale du cube):
donc soit donc donc

Salut Peacekeeper je passe te faire un petit coucou ^^
Tu donnes la solution bien vite dis-donc !

Julie

[Peacekeeper]

Salut Peacekeeper je passe te faire un petit coucou ^^
Tu donnes la solution bien vite dis-donc !

Julie

Relis les posts au-dessus, je l'ai guidée dans la résolution hier soir, elle voulait juste une récapitulation.

Ce n'est pas dans mon habitude de livrer la solution pieds et poings liés. :p

[almagathe]

On cherche l'arrête du petit cube, on l'appelle a.
Appliquons le théorème de Pythagore au triangle ABC (nomme-le comme tu veux, c'est le triangle constitué par 2 arrêtes et une diagonale de face). a²+a²=b² (en appelant b la longueur de la diagonale de face), donc

Appliquons maintenant le théorème de Pythagore au triangle ABD (l'autre triangle rectangle, celui constitué d'une arrête, d'une diagonale de face et d'une diagonale du cube):
donc soit donc donc

Alors là tu me sauves la vie ! Merci beaucoup !!!
Juste dans mon livre la consigne est " Calculer la longueur L des arrêtes de ce cube." est ce que L c'est comme si c'était a ?