[3e +] Fonctions - Calcul littéral - Exercices d'approfondissement

[Lostounet]

lol Vi vi je sais, j'étais en train d'éditer quand tu as posté. Okay.. Donc?

[Timothé Lefebvre]

Eh bien donc si x est impair (de la forme 2p+1) alors (x-1)=2p (pair),
(x-5)=2p-4 (pair) et n²+5=4p²+2p+6 (pair aussi). Or, le produit de trois nombres pairs est divisible par 8.

Conclusion, f(x) est un multiple de 8 pour tout x impair.

[Lostounet]

Ah :)
J'avais pas compris la question - mais ça y est. T'en as d'autres :') ?

[Timothé Lefebvre]

Oui, la deuxième partie de la question : déterminer l'ensemble des valeurs de x pour lesquelles f(x) est un multiple de 8 sans l'être de 16.

[Lostounet]

:S On commence par..? Nous on a trouvé que si x est impair, f(x) est un multiple de 8.. Mais il ne faut pas qu'il y ait "4" pairs.. .... .... ?
Mon problème est le fait que tu aies utilisé l'expression "pour quelles valeurs" qui me pose problème! On est pas en train de chercher des valeurs :S

[Timothé Lefebvre]

Si, on cherche l'ensemble des valeurs de x telles que f(x) soit multiple de 8 mais pas de 16.

[Lostounet]

On fait comment?

[Timothé Lefebvre]

Cherche :P
Je t'ai déjà fait la première partie de la question alors que tu devais t'y coller ^^

[Lostounet]

Des conseils.. des indices? Je suis encore en début troisième, et on n'a même pas travaillé les fonctions lol.

[Lostounet]

Je vais me contenter des factorisation :$

[Sve@r]

Des conseils.. des indices?

Des indices...
- 8 (1 * 8) correspond
- 16 (2 * 8) ne correspond pas
- 24 (3 * 8) correspond
- 32 (4 * 8) ne correspond pas
- 40 (5 * 8) correspond
T'arrives à en tirer une loi ???

[Lostounet]

Des indices...
- 8 (1 * 8) correspond
- 16 (2 * 8) ne correspond pas
- 24 (3 * 8) correspond
- 32 (4 * 8) ne correspond pas
- 40 (5 * 8) correspond
T'arrives à en tirer une loi ???

Le 8 est un produit de 3 pairs. En ajoutant un troisième pair, ça ne marche pas. En ajoutant un autre pair, ça marche. En rajoutant un autre, ça ne marche plus. Ainsi de suite..
MODIF: Il faut qu'on multiplie 8 par un impair?

MODIF 2: 8 est en fait le produit de 3 pairs.. Donc il s'agit ici de 3 pairs (Le 8) et d'un seul impair?

[Lostounet]

Désolé de remonter ce topic, mais j'ai une petite factorisation qui ne marche pas o_O.. (J'ai honte..).

La voici:
8x³ - 40x² + 50
Je prends 2 en facteur..
2 (4x³ - 20x² + 25)
2 ((2x)² - 2 * (2x) * 5 + (5)²) ?!
Il y a un "x" en moins... le cube pose problème. Merci de m'éclaircir. :)

P.S: D'autre part, on sait que 8x³ = (2x)³, mais ça n'a aucun rapport.. o_O?

[Zweig]

Je cherche des factorisations excessivement, extrêmement, impossiblement, parfaitement, formidablement, DIFFICILES (niveau 3ème surtout lol).

J'ai pas eu le courage de lire toutes ces pages, donc je pars du principe que tu recherches toujours des exercices de ce type.

i) Factorise
ii) Si tu es très courageux, factorise maintenant :

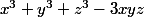
Bonne chance !

[Timothé Lefebvre]

ii) Si tu es très courageux, factorise maintenant :

Bonne chance !

Oh tiens, ça me rappelle une certaine inégalité non

[Zweig]

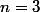
Héhé, oui, l'IAG dans le cas se démontre "simplement" en factorisant cette différence.

[Lostounet]

Euh euh euh!? Mais pourriez vous svp m'aider dans la mienne avant? lol
Ce que vous avez proposé est en rapport avec la mienne? O_o

[Timothé Lefebvre]

Ouaip c'est vrai, et ça se montre avec celle du réordonnement aussi (avec la symétrie) :id:

[Lostounet]

J'ai pas eu le courage de lire toutes ces pages, donc je pars du principe que tu recherches toujours des exercices de ce type.

i) Factorise
ii) Si tu es très courageux, factorise maintenant :

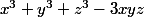
Bonne chance !

Hm...

(a-b)^3 + (c-b)^3 + (b-a)^3
= (a - b) (a - b) (a - b) + (c - b) (c - b) (c - b) + (b - a) (b - a) (b - a)

= (- 1) * (- a + b)³ + (- a + b)³ + (c - b) (c - b) (c - b)
NON DSL.. une sec.. lol

[Zweig]

Pour développer , utilise le fait que