[3e +] Fonctions - Calcul littéral - Exercices d'approfondissement
Réponses à toutes vos questions du CP à la 3ème
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 16:26
par Timothé Lefebvre » 01 Nov 2009, 16:26
Pour la réciproque tu ne peux pas vu que c'est ce que tu veux démontrer :lol2:

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 01 Nov 2009, 16:27
par Lostounet » 01 Nov 2009, 16:27
Je ne trouve pas l'erreur chez moi.. O_o
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 02 Nov 2009, 20:18
par Lostounet » 02 Nov 2009, 20:18
Je remonte le fil - il est important :D
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Nov 2009, 21:21
par Zweig » 02 Nov 2009, 21:21
Zweig a écrit:i) Factorise
^3 + (c-b)^3 + (b-a)^3)
ii) Si tu es très courageux, factorise maintenant :
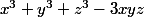
Je ne comprends pas trop tes développements ...
Pour l'exemple :
^3 = (a+b)(a^2 + 2ab+b^2) = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 = a^3 + 3a^2b + 3ab^2 + b^3)
Donc en remplaçant

par -

, on obtient :
^3 = a^3 - 3a^2b + 3ab^2 - b^3)
Par permutations circulaire, on obtient les autres développements. Il ne reste plus qu'à sommer et à factoriser.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 02 Nov 2009, 21:23
par Lostounet » 02 Nov 2009, 21:23
Euh Je n'ai pas développé.
J'ai juste remarqué que (a - b) et (b - a) sont opposés, leurs cubes le sont aussi donc. Non?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Nov 2009, 21:25
par Zweig » 02 Nov 2009, 21:25
Bah oui, et alors ? Enfin, je ne vois pas ce qui fait avancer le schmilblick, cette remarque.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 02 Nov 2009, 21:26
par Lostounet » 02 Nov 2009, 21:26
C'est une somme, on peut changer l'ordre des termes X_X.
Les opposés s'annulent, il ne reste que (c - b)³.. c'est tout prêt ! :P
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Nov 2009, 21:29
par Zweig » 02 Nov 2009, 21:29
Désolé, je me suis trompé. Voici l'énoncé corrigé :
i) Factorise
^3 + (b-c)^3 + (c-a)^3)
ii) Si tu es très courageux, factorise maintenant :
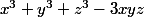

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 02 Nov 2009, 21:30
par Lostounet » 02 Nov 2009, 21:30
Bon, j'ferai demain, je dois y aller là :(
Merci :)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 08:53
par benekire2 » 03 Nov 2009, 08:53
Pour la i faut que tu fasse comme Zweig a dit, tu développe et ensuite tu remarque une identité remarquable de degré 3.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 03 Nov 2009, 12:38
par Zweig » 03 Nov 2009, 12:38
Sûrement pas ! En développant on ne retombe pas sur une identité remarquable de degré 3, sinon ce serait trop facile ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 13:00
par benekire2 » 03 Nov 2009, 13:00
Zweig a écrit:Sûrement pas ! En développant on ne retombe pas sur une identité remarquable de degré 3, sinon ce serait trop facile ...
Ah désolé, en lisant rapidement j'avais cru que si ^^ en plus on est dans ma section collège... Tu va le tuer le pauvre

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 03 Nov 2009, 16:00
par Lostounet » 03 Nov 2009, 16:00
lol
Pour factoriser, on considère P(x) = 0?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 16:02
par benekire2 » 03 Nov 2009, 16:02
Lostounet a écrit:lol
Pour factoriser, on considère P(x) = 0?
Ben en fait on factorise avec des racines... qui sont solutions de P(x) = 0

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 03 Nov 2009, 16:05
par Lostounet » 03 Nov 2009, 16:05
On peut donc parfaitement écrire:
(a-b)^3 + (b-c)^3 + (c-a)^3 = 0
Non? (Je ne sais pas si ça sert à quelque chose, au fond)
Merci beaucoup de ta participation :)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 16:11
par benekire2 » 03 Nov 2009, 16:11
non, ne l'écrit pas !!
Si on te dit de factoriser x²-9 t'as pas le droit d'écrire x²-9=0 !!
par contre comme -3 et 3 sont des racines ( et vérifient donc x²-9=0,) on peut écrire x²-9=(x-3)(x+3)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 03 Nov 2009, 16:12
par Lostounet » 03 Nov 2009, 16:12
Ah ok ok. Désolé :P
Bon euh.. je ne vois pas là lol..!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 16:14
par benekire2 » 03 Nov 2009, 16:14
lol c'est pas grave, c'est en se trompant qu'on apprend!!
( Les exos de sweig sont toujours difficiles ... )

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 03 Nov 2009, 16:15
par Lostounet » 03 Nov 2009, 16:15
Surtout pour un élève en début troisième! :P
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 16:37
par benekire2 » 03 Nov 2009, 16:37
oui, et je t'assure que pour les lycéens c'est pas facile non plus !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
