Bonjour toutes et tous, bonne année (il est encore temps)
Voila mon problème :
J'ai deux vecteurs aléatoires U et V, de dimension P. Je connais leurs matrices de variance - covariance, disons Su et Sv. De plus, leur espérance mathématique est nulle.
Je cherche à exprimer la variance du produit scalaire de ces deux vecteurs, c'est à dire :
Var( U' * V ) ; j'utilise le ' pour transposé
Pour les cas simples (Su et Sv diagonales), on arrive à montrer que Var(U' * V) = trace(Su * Sv)
Pour les cas quelconques, j'ai vérifié numériquement que la formule tient toujours, mais je n'arrive pas à la démontrer littéralement.
Quelqu'un peut il m'aider.
Merci d'avance
Jean-Michel
Variance d'un produit scalaire
9 messages
- Page 1 sur 1
J'insiste
par jean-michel.roger » 21 Jan 2011, 09:04
Vraiment personne n'est inspiré par ce problème ???
par fatal_error » 21 Jan 2011, 10:47
salut,
si U a pour espérance 0, alors
pour = 0)
Or pour construire S_u, on a la variance sur la diago, et
 = cov(X_i,X_j))
mais
 = E(X_i-E(X_i))E(X_j-E(X_j)))
et = 0)
... donc
 = E(X_i)E(X_j) = 0)
et on a forcément S_u diagonale non?
edit : mal lu les crochets sur wiki...
 = E(X_iX_j)...)
bref, encore un post useless
si U a pour espérance 0, alors
pour
Or pour construire S_u, on a la variance sur la diago, et
mais
et
et on a forcément S_u diagonale non?
edit : mal lu les crochets sur wiki...
bref, encore un post useless
la vie est une fête 
par fatal_error » 21 Jan 2011, 14:51
i am back.
alors
on garde
et pareil pour
on a par hypothèse
(1) = tr(S_u_{n-1})tr(S_v_{n-1}))
now on veut vérifier que c'est vrai pour tout n.
on note
on a (2)
On part de (1), et on va regarder comment)
est modifiée.
on a
(3) = tr(S_u_{n-1}S_v_{n-1}) + e + f)
avec
e les elem sur la diago pour i=1 à n-1, à ajouter à cause de la nouvelle variable X_n, (resp Y_n)
f l'elem sur la diago pour la nouvelle ligne ajoutée.
cov(Y_n,Y_i))
cov(Y_n,Y_j) + var(X_n)var(Y_n))
on déduit de (3) en substituant e et f
 = tr(S_u_{n-1}S_v_{n-1}) + 2 \bigsum_{i=1}^{n-1} cov(X_i,X_n)cov(Y_i,Y_n) + var(X_n)var(Y_n))
soit
ensuite on dev lexpression de (1) du coté gauche
=var(S_{n-1})+var(X_nY_n)+2cov(S_{n-1},X_nY_n))
et en cherchant l'égalité de (1) il faut prouver que qqsoit X_i, Y_i, s.c E(X_i)=E(Y_i)=0
(4)var(Y_n) + 2 \bigsum_{i=1}^{n-1} cov(X_i,X_n)cov(Y_i,Y_n) = var(Z_n)+2cov(S_{n-1},Z_n))
avec
apres on tente de faire apparaitre des E(X_i)=0 pour simplifier(4)
donc partant decov(Y_i,Y_n)=E(X_iX_n)E(Y_iY_n))
et = E(X_iY_iX_nY_n) - E(X_iX_n)E(Y_iY_n))
on déduitcov(Y_i,Y_n) = E(X_iY_iX_nY_n)-cov(X_iX_n, Y_iY_n))
next
soit (4) :var(Y_n) + 2 \bigsum_{i=1}^{n-1}E(X_iY_iX_nY_n)-cov(X_iX_n, Y_iY_n)= var(Z_n)+2cov(S_{n-1},Z_n))
on dév Z_n
=var(X_nY_n) = E(X_n^2Y_n^2)-E^2(X_nY_n)\\<br />var(Z_n) = E(X_n^2)E(Y_n^2)+cov(X_n^2,Y_n^2) - (E(X_n)E(Y_n) + cov(X_n,Y_n))^2\\<br />var(Z_n) = E(X_n^2)E(Y_n^2)+cov(X_n^2,Y_n^2) - cov^2(X_n,Y_n))
on développe de l'autre cotévar(Y_n) = E(X_n^2)E(Y_n^2) + E^2(X_n)E^2(Y_n) - E(X_n^2)E^2(Y_n)-E(Y_n^2)E^2(X_n) = E(X_n^2)E(Y_n^2) + 0)
(4) devient alors en simplifiant lesE(Y_n^2))
E:-cov(X_iX_n, Y_iY_n)= (cov(X_n^2,Y_n^2) - cov^2(X_n,Y_n))+2cov(S_{n-1},Z_n))
) = E^2(X_nY_n))
et =E(X_n^2Y_n^2)-E(X_n^2)E(Y_n^2))
donc - cov^2(X_n,Y_n)=var(Z_n) - E(X_n^2)E(Y_n^2))
Il vient alors
E(Y_n^2) + 2 \bigsum_{i=1}^{n-1}E(X_iY_iX_nY_n)-cov(X_iX_n, Y_iY_n)= var(Z_n)+2cov(S_{n-1},Z_n))
puis = \bigsum_{i=1}^{n-1}cov(X_iY_i,X_nY_n))
donc
E :E(Y_n^2) + 2 \bigsum_{i=1}^{n-1}\left( E(X_iY_iX_nY_n)-cov(X_iX_n, Y_iY_n)-cov(X_iY_i,X_nY_n)\right)= var(Z_n))
 = cov(X_iX_n,Y_iY_n) + E(X_iX_n)E(Y_iY_n))
ou
 = cov(X_iY_i,X_nY_n) + E(X_iY_i)E(X_nY_n))
donc on a le choix pour E : either
E:E(Y_n^2) +2 \bigsum_{i=1}^{n-1}(E(X_iX_n)E(Y_iY_n) - cov(X_iY_i,X_nY_n) = var(Z_n))
or
E :E(Y_n^2) +2 \bigsum_{i=1}^{n-1}(E(X_iY_i)E(X_nY_n) - cov(X_iX_n, Y_iY_n) = var(Z_n))
reste à montrer que le gros paté à gauche ca vaut)
:marteau:
mais bon, jvais marreter là, je sais même pas si ca aboutit et si ya pas des couilles qui se sont glissées.
alors
on garde
on a par hypothèse
(1)
now on veut vérifier que c'est vrai pour tout n.
on note
on a (2)
On part de (1), et on va regarder comment
on a
(3)
avec
e les elem sur la diago pour i=1 à n-1, à ajouter à cause de la nouvelle variable X_n, (resp Y_n)
f l'elem sur la diago pour la nouvelle ligne ajoutée.
on déduit de (3) en substituant e et f
soit
ensuite on dev lexpression de (1) du coté gauche
et en cherchant l'égalité de (1) il faut prouver que qqsoit X_i, Y_i, s.c E(X_i)=E(Y_i)=0
(4)
avec
apres on tente de faire apparaitre des E(X_i)=0 pour simplifier(4)
donc partant de
et
on déduit
next
soit (4) :
on dév Z_n
on développe de l'autre coté
(4) devient alors en simplifiant les
E:
et
donc
Il vient alors
puis
donc
E :
ou
donc on a le choix pour E : either
E:
or
E :
reste à montrer que le gros paté à gauche ca vaut
mais bon, jvais marreter là, je sais même pas si ca aboutit et si ya pas des couilles qui se sont glissées.
la vie est une fête
une piste?
par jean-michel.roger » 21 Jan 2011, 14:53
Bon, pour faire avancer le schmilblick, voici ce que j'ai "réussi" à faire, qui aide dans le cas où Su et Sv sont diagonales :
Je suppose que
et 
peuvent s'écrire :
et
où
et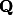 
sont des vecteurs gaussiens dont chaque composante est indépendante des autres, d'espérance nulle et de variance 1.
Le produit scalaire
s'écrit alors :
Dans le cas où
et 
sont diagonales, il vient rapidement que  = trace( \mathbf{S_u} \mathbf{S_v} ))
Est ce que je me trompe?
Est ce que cela vous met sur une piste ?
Merci d'avance de votre aide
Jean Michel
Je suppose que
et
où
Le produit scalaire
Dans le cas où
Est ce que je me trompe?
Est ce que cela vous met sur une piste ?
Merci d'avance de votre aide
Jean Michel
par fatal_error » 21 Jan 2011, 15:07
mon petit doigt me dit que c'est un probleme qui me dépasse...
bonne chance qd même
bonne chance qd même
la vie est une fête
par Ben314 » 21 Jan 2011, 16:32
Salut,
Je comprend vraiment pas comment le résultat pourrait être vrai en général : pour calculer le trace de Su*Sv, il n'est pas utile de savoir s'il y a une quelconque corélation entre les vecteurs aléatoires U et V alors qu'il me semble évident que la valeur du produit scalaire de U avec V dépend fortement des éventuelles corélations entre U et V.
Par exemple, si U ne prend que deux valeurs orthogonales E1 ou E2 (avec proba 1/2) et que V ne prend lui aussi que ces deux mêmes valeurs E1 ou E2 (avec proba 1/2) alors :
- Si par exemple U=E1 V=E1 alors =||E1||² ou ||E2||² (avec proba 1/2) et la variance de est non nulle si ||E1||||E2||.
- Si par contre on a U=E1 V=E2 alors =0 (avec proba 1)...
Si par contre tu suppose les vecteurs U et V indépendants, alors le résultat me semble assez évident :
Si_i)
et _i)
alors \big)_{i,j})
, \big)_{i,j})
donc =\sum_{i,j}E(X_iX_j)E(Y_iY_j))
Si
alors =\sum_iE(X_iY_i)=\sum_iE(X_i)E(Y_i))
(grâce à l'hypothèse d'indépendance) donc =0)
et  =E(Z^2) =E\Big(\sum_{i,j}X_iY_iX_jY_j\Big) =\sum_{i,j}E(X_iY_iX_jY_j)<br />=\sum_{i,j}E(X_iX_j)E(Y_iY_j))
(grâce à l'hypothèse d'indépendance)
Je comprend vraiment pas comment le résultat pourrait être vrai en général : pour calculer le trace de Su*Sv, il n'est pas utile de savoir s'il y a une quelconque corélation entre les vecteurs aléatoires U et V alors qu'il me semble évident que la valeur du produit scalaire de U avec V dépend fortement des éventuelles corélations entre U et V.
Par exemple, si U ne prend que deux valeurs orthogonales E1 ou E2 (avec proba 1/2) et que V ne prend lui aussi que ces deux mêmes valeurs E1 ou E2 (avec proba 1/2) alors :
- Si par exemple U=E1 V=E1 alors =||E1||² ou ||E2||² (avec proba 1/2) et la variance de est non nulle si ||E1||||E2||.
- Si par contre on a U=E1 V=E2 alors =0 (avec proba 1)...
Si par contre tu suppose les vecteurs U et V indépendants, alors le résultat me semble assez évident :
Si
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Résolu !!
par jean-michel.roger » 21 Jan 2011, 22:37
J'avais effectivement oublié de préciser que U et V étaient eux mêmes indépendants.
Merci beaucoup Ben134 pour cette démonstration, parfaitement claire §
Bon week end à tous
Jean-Michel
Merci beaucoup Ben134 pour cette démonstration, parfaitement claire §
Bon week end à tous
Jean-Michel
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :