A propos de la diversité des Alephs
96 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
A propos de la diversité des Alephs
Bonjour à tous. Un aspect des mathématiques me pose problème.
Comment la notion unique d'infini engendre-t-elle différents Alephs ?
Autrement dit, comment l'infini peut-il disposer de divers et multiples cardinaux ?
Est-ce parce qu'il existe différents ensembles infinis en mathématique ?
Cela n'a pas de sens dans mon esprit. Pouvez-vous éclaircir mon esprit au sujet des Alephs ?
Comment la notion unique d'infini engendre-t-elle différents Alephs ?
Autrement dit, comment l'infini peut-il disposer de divers et multiples cardinaux ?
Est-ce parce qu'il existe différents ensembles infinis en mathématique ?
Cela n'a pas de sens dans mon esprit. Pouvez-vous éclaircir mon esprit au sujet des Alephs ?
Re: A propos de la diversité des Alephs
c'est exactement cela, il ya plusieurs infinis.
Avec IN, tu peux compter, dénombrer ton infini,
par exemple tu peux compter combien tu as de nombres pairs,
alors tu prononces 1 , 2,3,4,5,6,7,... à chaque fois que tu vois un nombre pair.
Tu peux aussi physiquement taper du doigt et battre la mesure à chaque fois que tu vois un nombre pair, comme tu pourrais appuyer sur une touche + puis + puis +
ou la touche suivant, suivant suivant, suivant.
Maintenant avec les entiers IN tu ne pourras pas compter IR, tu ne pourras pas compter les nombres réels entre 0 et 1,...tu pourras pas faire suivant , suivant suivant...c'est pas dénombrable.
Avec IN, tu peux compter, dénombrer ton infini,
par exemple tu peux compter combien tu as de nombres pairs,
alors tu prononces 1 , 2,3,4,5,6,7,... à chaque fois que tu vois un nombre pair.
Tu peux aussi physiquement taper du doigt et battre la mesure à chaque fois que tu vois un nombre pair, comme tu pourrais appuyer sur une touche + puis + puis +
ou la touche suivant, suivant suivant, suivant.
Maintenant avec les entiers IN tu ne pourras pas compter IR, tu ne pourras pas compter les nombres réels entre 0 et 1,...tu pourras pas faire suivant , suivant suivant...c'est pas dénombrable.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: A propos de la diversité des Alephs
et après il ya le lycée de Versailles.
Avec les nombres pairs tu peux compter tous les entiers, suffit de changer un peu les noms, tu dis
0,2,4,6,8,10 quand tu vois 0,1,2,3,4,5
ça fait toc, toc, toc, toc, suivant suivant, mais comme des nombres pairs tu en as autant que tu veux tu ne seras pas coincé pour changer les noms.
Et aussi il ya autant de points dans un segment que dans le droite entiere, que dans le plan
Là faut taper google Cantor,
bijection des infinis.
le plus joli étant la lettre de Cantor à son ami mathématicien où cantor lui dit je me pince, mais pince moi plus fort, c'est-y pas vrai que j'ai une bijection du petit bout avec la droite...Grand moment de l'histoire des maths, de l'histoire des sciences cette lettre!
Avec les nombres pairs tu peux compter tous les entiers, suffit de changer un peu les noms, tu dis
0,2,4,6,8,10 quand tu vois 0,1,2,3,4,5
ça fait toc, toc, toc, toc, suivant suivant, mais comme des nombres pairs tu en as autant que tu veux tu ne seras pas coincé pour changer les noms.
Et aussi il ya autant de points dans un segment que dans le droite entiere, que dans le plan
Là faut taper google Cantor,
bijection des infinis.
le plus joli étant la lettre de Cantor à son ami mathématicien où cantor lui dit je me pince, mais pince moi plus fort, c'est-y pas vrai que j'ai une bijection du petit bout avec la droite...Grand moment de l'histoire des maths, de l'histoire des sciences cette lettre!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: A propos de la diversité des Alephs
Merci, beagle, pour cette superbe explication !
Il y a donc différentes manières de voir l'Infini….
En outre, est-il possible de comparer les Alephs entre eux en instaurant une relation d'ordre dans l'ensemble des Alephs ?
Par exemple, l'Aleph de l'ensemble des Réels est-il supérieur à l'Aleph de l'ensemble des Entiers Naturels ????
Il y a donc différentes manières de voir l'Infini….
En outre, est-il possible de comparer les Alephs entre eux en instaurant une relation d'ordre dans l'ensemble des Alephs ?
Par exemple, l'Aleph de l'ensemble des Réels est-il supérieur à l'Aleph de l'ensemble des Entiers Naturels ????
Modifié en dernier par grantstewart le 19 Juil 2018, 14:56, modifié 1 fois.
Re: A propos de la diversité des Alephs
je vais laisser les autres répondre,
en matière de relation d'ordre c'est toi qui m'a épaté hier suite à la réponse de hdci,
donc sur les terminologies je laisse les copains répondre,
j'ai une licence amateur seulement, pas pro!
en matière de relation d'ordre c'est toi qui m'a épaté hier suite à la réponse de hdci,
donc sur les terminologies je laisse les copains répondre,
j'ai une licence amateur seulement, pas pro!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: A propos de la diversité des Alephs
Oui, les différents infinis sont hiérarchisés.
Pour faire simple : le premier infini est l'infini dénombrable, c'est celui de (et de
(et de 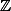 ,
, 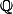 car ces ensembles sont en bijection les uns avec les autres). (D'un point de vue plus formel, le cardinal d'un ensemble est le plus petit ordinal avec lequel l'ensemble peut être mis en bijection).
car ces ensembles sont en bijection les uns avec les autres). (D'un point de vue plus formel, le cardinal d'un ensemble est le plus petit ordinal avec lequel l'ensemble peut être mis en bijection).
Par contre, on montre que) , l'ensemble des parties de
, l'ensemble des parties de  , est de cardinal strictement plus grand que celui de
, est de cardinal strictement plus grand que celui de  (autrement dit : il n'existe pas de bijection entre
(autrement dit : il n'existe pas de bijection entre ) et
et  , mais il y a une injection canonique de
, mais il y a une injection canonique de  dans
dans ) ).
).
Ceci est vrai d'ailleurs pour tous les ensembles : il n'y a pas de bijection entre un ensemble et l'ensemble de ses parties. Donc le cardinal de)) est strictement plus grand que celui de
est strictement plus grand que celui de )
Et caetera...
On montre également (c'est un peu plus ardu mais accessible) que a le même cardinal que
a le même cardinal que )
Une grande question est : y a-t-il un cardinal strictement compris entre celui de et celui de
et celui de  ? A cette question, des mathématiciens géniaux (ou fous ?) ont démontré que c'était indécidable : c'est-à-dire, que si la théorie des ensembles (ZFC pour les intimes) à laquelle on ajoute l'axiome "il existe un cardinal strictement compris entre
? A cette question, des mathématiciens géniaux (ou fous ?) ont démontré que c'était indécidable : c'est-à-dire, que si la théorie des ensembles (ZFC pour les intimes) à laquelle on ajoute l'axiome "il existe un cardinal strictement compris entre  et
et  " est cohérente, alors la théorie ZFC à laquelle on ajoute l'axiome "il n'y a pas de cardinal strictement compris entre
" est cohérente, alors la théorie ZFC à laquelle on ajoute l'axiome "il n'y a pas de cardinal strictement compris entre  et
et  " est également cohérente.
" est également cohérente.
Du coup, décider s'il y en a un ou pas, c'est une question d'axiome : c'est ce qu'on appelle "l'hypothèse du continu" (il n'y a pas de cardinal entre et
et  ), ou encore plus fort, "hypothèse du continu généralisé" qui dit qu'il n'y a pas de cardinal strictement compris entre un ensemble infini et l'ensemble de ses parties.
), ou encore plus fort, "hypothèse du continu généralisé" qui dit qu'il n'y a pas de cardinal strictement compris entre un ensemble infini et l'ensemble de ses parties.
Pour faire simple : le premier infini est l'infini dénombrable, c'est celui de
Par contre, on montre que
Ceci est vrai d'ailleurs pour tous les ensembles : il n'y a pas de bijection entre un ensemble et l'ensemble de ses parties. Donc le cardinal de
Et caetera...
On montre également (c'est un peu plus ardu mais accessible) que
Une grande question est : y a-t-il un cardinal strictement compris entre celui de
Du coup, décider s'il y en a un ou pas, c'est une question d'axiome : c'est ce qu'on appelle "l'hypothèse du continu" (il n'y a pas de cardinal entre
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: A propos de la diversité des Alephs
Bravo hdc !
C'est, à nouveau, Toi qui remportes l'énigme mathématique des Alephs….
C'est, à nouveau, Toi qui remportes l'énigme mathématique des Alephs….
Re: A propos de la diversité des Alephs
grantstewart a écrit:Bravo hdc !
C'est, à nouveau, Toi qui remportes l'énigme mathématique des Alephs….
Ptain y va mettre une relation d'ordre dans les réponses de chacun de ses fils?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: A propos de la diversité des Alephs
Afin de poursuivre cette conversation sur les Alephs, voici une question compliquée...
J'ai l'habitude de donner des notes supérieures à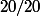 à certains de mes élèves...
à certains de mes élèves...
Ai-je le droit d'utiliser la note de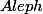 -ω
-ω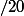 ?
?
La grandeur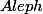 -ω est-elle compatible avec l'entier naturel
-ω est-elle compatible avec l'entier naturel 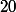 ?
?
J'ai l'habitude de donner des notes supérieures à
Ai-je le droit d'utiliser la note de
La grandeur
Re: A propos de la diversité des Alephs
aucun problème, tu iras plus vite pour faire les moyennes trimestrielles.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: A propos de la diversité des Alephs
beagle a écrit:aucun problème, tu iras plus vite pour faire les moyennes trimestrielles.
C'est clair !
Plus besoin de calculer quoi que ce soit !
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: A propos de la diversité des Alephs
J'ai l'impression que les Alephs ne jouent qu'à augmenter l'infini,
ne le diminuant pas. En effet, je ne trouve nulle part de trace
de la notion d') ,
, ) ,
, ) .
.
Savez-vous si cette soustraction d'entiers à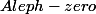 est
est
pertinente et existe dans les mathématiques ?
ne le diminuant pas. En effet, je ne trouve nulle part de trace
de la notion d'
Savez-vous si cette soustraction d'entiers à
pertinente et existe dans les mathématiques ?
Re: A propos de la diversité des Alephs
Salut,
Le problème, c'est qu'il faudrait peut être songer à "remettre les pieds sur terre" :
L'infini, sous quelque forme que ce soit, n'a aucune existence concrète, donc c'est de la "pure (et dure) abstraction" avec lequel tu ne peut bien évidement travailler qu'avec un formalisme parfaitement clair et précis (il est bien évident que tu risque pas de dire quoi que ce soit "d'intuitif" concernant un truc qui n'a pas la moindre existence concrète).
Donc, si tu veut un tant soit peu "manipuler" des trucs comme les cardinaux infinis, il faut forcément avoir une définition rigoureuse de ce que sont ces fameux aleph ainsi que des définition tout aussi rigoureuse des opérations que tu va accepter de faire dessus.
Bref,
1) La définition d'un cardinal, c'est une classe d'ensemble modulo la relation d'équipotence (i.e. il existe une bijection entre les deux ensembles).
2) On peut démontrer que, si A et B sont deux ensemble disjoints ainsi que A' et B' avec A équipotent à A' et B équipotent à B' alors les ensembles AuB et A'uB' sont équipotents. Et ce constat fait que le cardinal d'une réunion (disjointe) ne dépend que des cardinaux des deux ensembles en question ce qui permet de définir une notion d'addition sur les cardinaux (égal au cardinal d'une réunion disjointe).
3) Sauf que, si tu veut faire à peu prés la même chose pour définir une notion de soustraction en disant que le cardinal de A moins le cardinal de B, ça va être le cardinal de l'ensemble A privé de B (ou on suppose que A contient B), ben c'est clairement débile vu que là, le cardinal de A privé de B ne dépend pas uniquement du cardinal de A et de B :
- Si A=N et B=N (tout les deux de cardinal dénombrable) alors A privé de B, c'est l'ensemble vide de cardinal 0.
- Si A=N et B=N* (tout les deux de cardinal dénombrable) alors A privé de B, c'est {0} cardinal 1.
- Si A=N et B={nombres pairs} (tout les deux de cardinal dénombrable) alors A privé de B, c'est {nombres impairs} de cardinal dénombrable.
Donc, pour que ta "soustraction" ait du sens, il faut être dans une configuration où le cardinal de A privé de B ne dépend que du cardinal de A et de B et pas d'autre chose ce qui est vrai :
- Lorsque A et B sont finis (et c'est pour ça que ça a du sens de faire la soustraction de deux entiers et c'est bien sous cette forme de "cardinal de A privé de B" que c'est présenté dans le primaire).
- Lorsque A est infini et que le cardinal de B est strictement inférieur à celui de A où le cardinal de A privé de B sera systématiquement celui de A. (par exemple un cardinal infini "moins" un cardinal fini, ça fait systématiquement le cardinal de départ).
Le problème, c'est qu'il faudrait peut être songer à "remettre les pieds sur terre" :
L'infini, sous quelque forme que ce soit, n'a aucune existence concrète, donc c'est de la "pure (et dure) abstraction" avec lequel tu ne peut bien évidement travailler qu'avec un formalisme parfaitement clair et précis (il est bien évident que tu risque pas de dire quoi que ce soit "d'intuitif" concernant un truc qui n'a pas la moindre existence concrète).
Donc, si tu veut un tant soit peu "manipuler" des trucs comme les cardinaux infinis, il faut forcément avoir une définition rigoureuse de ce que sont ces fameux aleph ainsi que des définition tout aussi rigoureuse des opérations que tu va accepter de faire dessus.
Bref,
1) La définition d'un cardinal, c'est une classe d'ensemble modulo la relation d'équipotence (i.e. il existe une bijection entre les deux ensembles).
2) On peut démontrer que, si A et B sont deux ensemble disjoints ainsi que A' et B' avec A équipotent à A' et B équipotent à B' alors les ensembles AuB et A'uB' sont équipotents. Et ce constat fait que le cardinal d'une réunion (disjointe) ne dépend que des cardinaux des deux ensembles en question ce qui permet de définir une notion d'addition sur les cardinaux (égal au cardinal d'une réunion disjointe).
3) Sauf que, si tu veut faire à peu prés la même chose pour définir une notion de soustraction en disant que le cardinal de A moins le cardinal de B, ça va être le cardinal de l'ensemble A privé de B (ou on suppose que A contient B), ben c'est clairement débile vu que là, le cardinal de A privé de B ne dépend pas uniquement du cardinal de A et de B :
- Si A=N et B=N (tout les deux de cardinal dénombrable) alors A privé de B, c'est l'ensemble vide de cardinal 0.
- Si A=N et B=N* (tout les deux de cardinal dénombrable) alors A privé de B, c'est {0} cardinal 1.
- Si A=N et B={nombres pairs} (tout les deux de cardinal dénombrable) alors A privé de B, c'est {nombres impairs} de cardinal dénombrable.
Donc, pour que ta "soustraction" ait du sens, il faut être dans une configuration où le cardinal de A privé de B ne dépend que du cardinal de A et de B et pas d'autre chose ce qui est vrai :
- Lorsque A et B sont finis (et c'est pour ça que ça a du sens de faire la soustraction de deux entiers et c'est bien sous cette forme de "cardinal de A privé de B" que c'est présenté dans le primaire).
- Lorsque A est infini et que le cardinal de B est strictement inférieur à celui de A où le cardinal de A privé de B sera systématiquement celui de A. (par exemple un cardinal infini "moins" un cardinal fini, ça fait systématiquement le cardinal de départ).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: A propos de la diversité des Alephs
Cher Ben314, toutes tes explications dépassent mon entendement.
Elles ont l'air cohérentes, mais je ne dispose pas d'un niveau mathématique suffisamment élevé afin de les comprendre pleinement.
Je vais simplifier ma question.
Je sais que l'on peut écrire) ,
, ) ,
, ) ,
, ) …
…
Mais est-il possible d'écrire) ,
, ) ,
, ) ... ?
... ?
Elles ont l'air cohérentes, mais je ne dispose pas d'un niveau mathématique suffisamment élevé afin de les comprendre pleinement.
Je vais simplifier ma question.
Je sais que l'on peut écrire
Mais est-il possible d'écrire
Re: A propos de la diversité des Alephs
Si tu as pas les outils (formels) nécessaire à la compréhension des définition de ce que sont les cardinaux infinis, alors tu va droit dans le mur : tout ce qui est raisonnement intuitif est totalement et on ne peut plus clairement "à bannir".grantstewart a écrit:Cher Ben314, toutes tes explications dépassent mon entendement.
Elles ont l'air cohérentes, mais je ne dispose pas d'un niveau mathématique suffisamment élevé afin de les comprendre pleinement.
C'est pas pour rien que Cantor (le père des cardinaux) a créé autant de controverse à son époque et que beaucoup de ces contemporains dont de très très illustre mathématiciens de l'époque considéraient que c'était totalement délirant comme point de vue de considérer comme formant "un tout" une collection infinie d'objets.
Modifié en dernier par Ben314 le 30 Oct 2018, 17:10, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: A propos de la diversité des Alephs
Ben314 a écrit:C'est pas pour rien que Cantor (le père des cardinaux) a créé autant de controverse à son époque et que beaucoup de ces contemporains dont de très très illustre mathématiciens de l'époque considéraient que c'était totalement délirant comme point de considérer comme formant "un tout" une collection infinie d'objets.
Ben314, tu ne réponds, là, aucunement à ma question, qui est la suivante :
Est-il possible d'écrire
Re: A propos de la diversité des Alephs
Bonjour,
Il est toujours possible de l'écrire, la preuve, tu viens de le faire.
En revanche, est-ce que cela a un sens? Quel sens donnerais tu à ce que tu viens d'écrire?
Ben pour ça, j'ai bien peur qu'il faille que tu aies "un niveau mathématique suffisant" ... Mais même si ce n'est pas le cas, c'est intéressant de chercher.
Et je dirais : non cela n'a pas de sens.
Les Aleph sont le cardinal des ensembles infinis. Il faut donc bien comprendre le concept de cardinal (et donc de relation d'équivalence)
Aleph zero n'est qu'une notation pour dire " le plus petit cardinal infini"
Il est toujours possible de l'écrire, la preuve, tu viens de le faire.
En revanche, est-ce que cela a un sens? Quel sens donnerais tu à ce que tu viens d'écrire?
Ben pour ça, j'ai bien peur qu'il faille que tu aies "un niveau mathématique suffisant" ... Mais même si ce n'est pas le cas, c'est intéressant de chercher.
Et je dirais : non cela n'a pas de sens.
Les Aleph sont le cardinal des ensembles infinis. Il faut donc bien comprendre le concept de cardinal (et donc de relation d'équivalence)
Aleph zero n'est qu'une notation pour dire " le plus petit cardinal infini"
Re: A propos de la diversité des Alephs
Bravo & merci pour cette réponse compétente & pertinente, LB2...
Prenons un exemple.
Admettons un intervalle de temps de 682 années de l'an 2018 à l'an 2700.
En 2018, il reste 682 années afin d'atteindre l'an 2700.
En 2700, il restera) années afin d'atteindre l'an
années afin d'atteindre l'an  .
.
En 2018, il reste) années afin d'atteindre l'an
années afin d'atteindre l'an  .
.
Et l'an prochain, en 2019, il restera) années afin d'atteindre l'an
années afin d'atteindre l'an  .
.
Si on peut soustraire une année à) ,
,
c'est que l'on peut soustraire une année à) , ce qui donne
, ce qui donne ) .
.
Cela est-il correct, LB2 ? Vois-tu où je veux en venir ?
LB2 a écrit:En revanche, est-ce que cela a un sens ? Quel sens donnerais tu à ce que tu viens d'écrire ?
Prenons un exemple.
Admettons un intervalle de temps de 682 années de l'an 2018 à l'an 2700.
En 2018, il reste 682 années afin d'atteindre l'an 2700.
En 2700, il restera
En 2018, il reste
Et l'an prochain, en 2019, il restera
Si on peut soustraire une année à
c'est que l'on peut soustraire une année à
Cela est-il correct, LB2 ? Vois-tu où je veux en venir ?
Re: A propos de la diversité des Alephs
as-tu l'age suffisant pour parler de l'an +l'infini?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
96 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
