Premiers classés par niveau

[R.E.]

Bonjour,

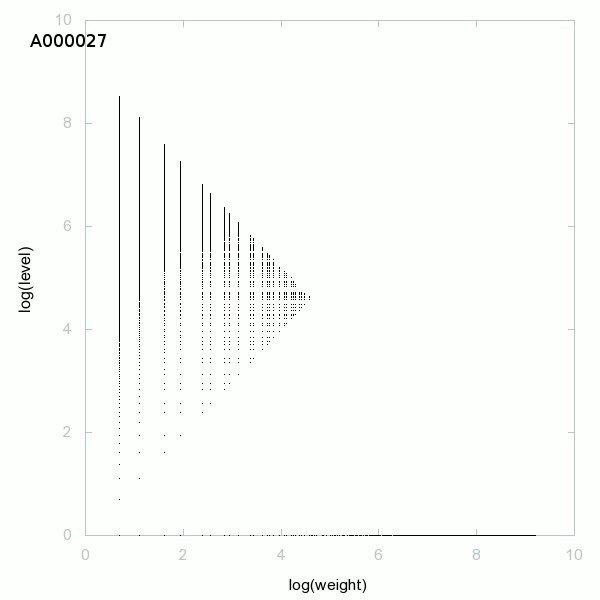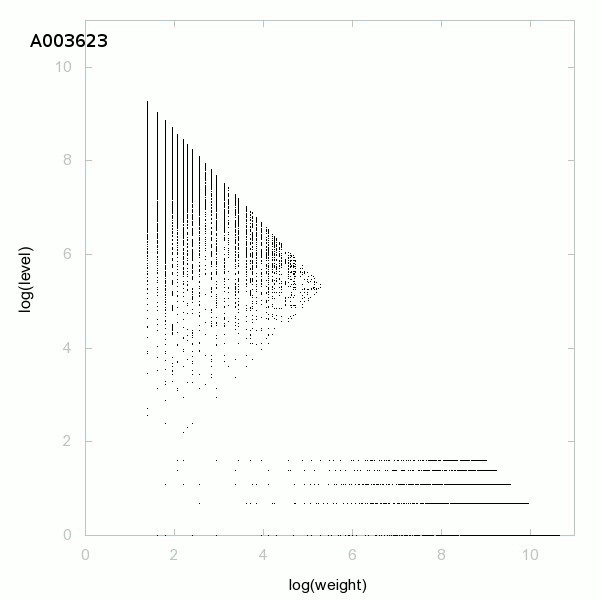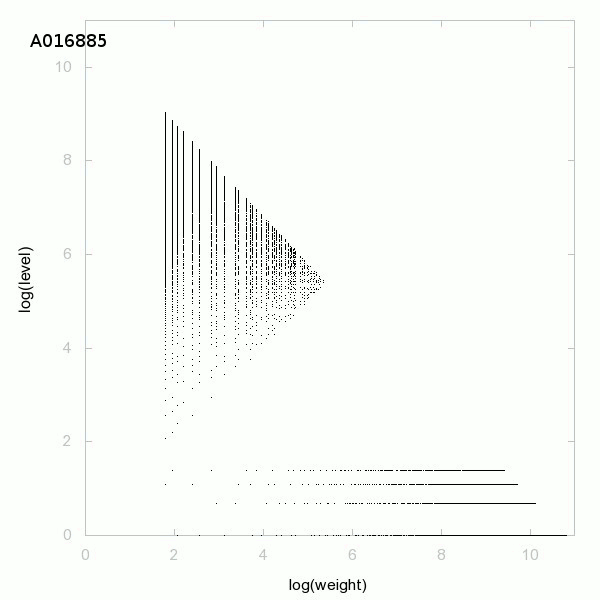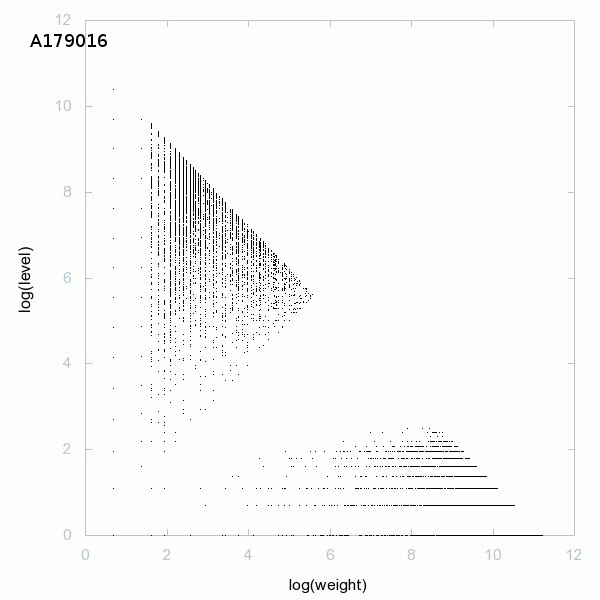
Je vous propose une conjecture dont les définitions seront données un peu plus bas :
Conjecture 9 : les nombres premiers classés par niveau se raréfient parmi les nombres premiers.

Précisions importantes : à part , et les nombres premiers sont soit classés par poids soit par niveau. Les nombres premiers classés par poids ont par définition un saut (première différence) inférieur à

Mes questions sont :
- Cette conjecture est-elle dure à prouver ? (je pense que oui)
- Cette conjecture est-elle intéressante concernant la répartition des nombres premiers ? (je pense que oui)
- Quelles sont les relations de cette conjecture avec d'autres conjectures célèbres comme la conjecture de Legendre et l'hypothèse de Riemann ?

Je mets les définitions de la décomposition en sur le forum pour que vous n'ayez pas à sortir mais vous pouvez les retrouver sur la page de la décomposition sur l'OEISWiki et dans mon preprint (arXiv:0711.0865)

Définitions de la décomposition en :

Soit une suite d'entier strictement croissante.

Le saut (première différence, écart) :




Définition alternative avec la fonction :



Le poids :

Définition alternative avec la fonction :


Le niveau :



Critère de décomposition :
La décomposition est possible si et seulement si

Une décomposition unique :
Le poids est le plus petit tel que dans la division euclidienne de par son poids, le quotient est le niveau et le reste est le saut et nous avons :

Principe de classification :
Si pour alors n'est pas classé.
Si pour est classé par niveau sinon est classé par poids.

La décomposition en des entiers naturels est le crible d’Ératosthène : les entiers naturels classés par poids sont les et ceux classés par niveau sont les


Ci-dessous un graphique de la décomposition des nombres premiers :


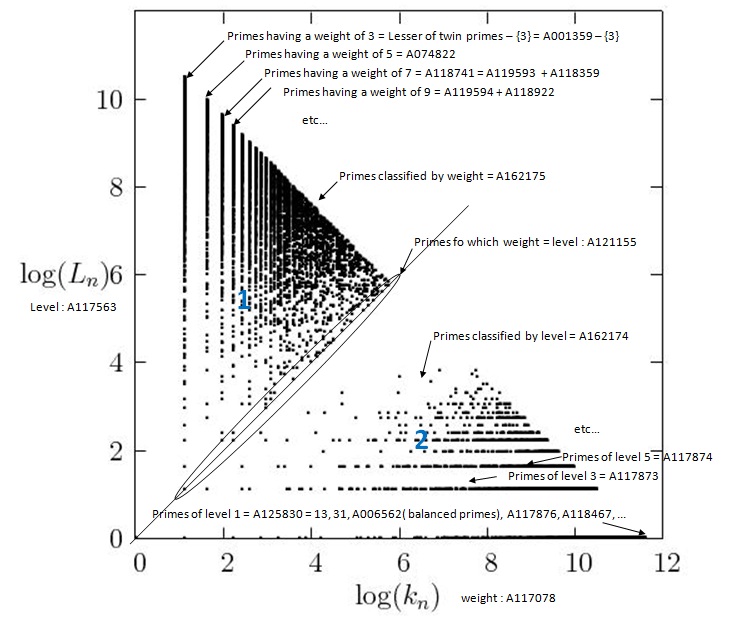
Cela fait pas mal de temps que j'ai compris que je ne faisais pas des maths car faire des mathématiques c'est démontrer des propositions or je ne fais que monter une façon de décomposer les nombres. Dans mon preprint, ce ne sont pas les théorèmes et lemmes qui sont importants mais les définitions.

Merci d'avoir pris le temps de lire ce message,

Rémi.

[R.E.]

Bonjour,

150 suites décomposées en un gif :


Ma première suite : A117078 (celle dont tout découle - 10 ans aujourd'hui).

La décomposition en poids × niveau + saut des nombres premiers en 3D (WebGL-three.js).

Un album Google+ des graphiques 2D des 400 suites que j'ai décomposées.

Mes questions du premier post tiennent toujours.

Bonne journée,

Rémi.

[R.E.]

Bonjour,

La décomposition en est une décomposition d'entier positif dans une suite. Le poids est le plus petit tel que dans la division euclidienne d'un nombre par son poids, le reste et le saut (première différence, écart). Le quotient est le niveau. Donc pour décomposer , on a besoin de avec (suite strictement croissante) et la décomposition est possible si .
La décomposition en des entiers naturels est le crible d’Ératosthène. Pour les entiers naturels, le poids est plus plus petit facteur premier de et le niveau est le plus grand diviseur propre de . Les entiers naturels classés par niveau sont les et les entiers naturels classés par poids sont les .
Pour les nombres premiers, cette décomposition conduit à une nouvelle classification des nombres premiers. Les nombres premiers classés par poids suivent le conjecture de Legendre et je conjecture que ceux classés par niveau se raréfient. Je pense que cette conjecture est très importante pour la distribution des nombres premiers. Il est facile de voir et de prouver que les plus petits des nombres premiers jumeaux () ont un poids de . Donc la conjecture des nombres premiers jumeaux peut se réécrire : il y a une infinité de nombres premiers qui ont un poids de .
Je ne suis pas mathématicien donc je décompose des suites pour promouvoir ma vision des nombres, maintenant 400 suites décomposées sur mon site avec les 500 premiers termes et des graphiques en 3D (webGL - three.js). En faisant ces décompositions, j'applique une sorte de crible sur chacune de ces suites. En un sens, je trouve les composés (nombres classés par poids) et les premiers (nombres classés par niveau) de chacune de ces suites.

Un album imgur.

Bonne journée,

R.E.