Les racines négatives existent, pourquoi pas les dénominateu
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 16:25
par Dinozzo13 » 05 Mai 2010, 16:25
Bonjour, ça fait un moment que je me pose cette question et j'aimerais savoir ce que vous en pensez :
Pourrais-t-on remplacer un dénominateur nul par une lettre tout comme les racines négatives qu'on les écris en fonction de
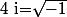
?
ex : si on pose :

.
Et puis je me dis, admettre l'existence des racines négatives implique un nouvel ensemble dont l'élément je dirai "caractéristique" est i ; donc si on admet qu'un dénominateur peut-être nul on aurait alors un nouvel ensemble , (
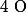
tel que
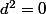
? biensûr j'invente ^^).
Et donc par ex : pour tout

de
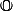
:
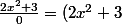d)
d=2dx^2)
Alors après est-ce que
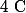
serait inclus dans
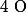
ou l'inverse ou ni l'un ni l'autre ? Je n'en sais rien.
En tout cas
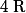
serait inclus dans
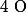
.
Biensûr je comprends tout à fait que cette idée peut paraître farfelue, mais qui sait, on disait déjà la même chose des complexes :party:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 05 Mai 2010, 16:55
par Ericovitchi » 05 Mai 2010, 16:55
le problème de poser d=1/0 c'est que ça bousille la notion d'élément neutre 0 dans le corps des réels puisque ça entraîne d fois 0 = 1 qui est contraire à la définition d'un élément neutre pour la multiplication.
Donc ça n'a plus une structure de corps. Il faudrait trouver un nouvel élément neutre, ou une nouvelle opération remplaçant la multiplication (commutative, distributive sur l'addition, etc, etc... ).
Donc ça ne va pas, ça ne laisse pas intègre les définitions des opérations.
tu devrais t'intéresser aux quaternions plutôt, si tu veux jouer au chercheur de nouvelles structures.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 05 Mai 2010, 16:57
par anthony_unac » 05 Mai 2010, 16:57
Dinozzo13 a écrit:Bonjour, ça fait un moment que je me pose cette question et j'aimerais savoir ce que vous en pensez :
Pourrais-t-on remplacer un dénominateur nul par une lettre tout comme les racines négatives qu'on les écris en fonction de
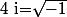
?
ex : si on pose :

.
Mais alors dans ce cas si d=1/0 "alors" 1=d*0 or 1 ne peut pas être égal à zéro puisque 1 est le succésseur de zéro.
Je poursuis encore :
2*d = 2*1/0 = 2/0 "donc" 2 = 0*2*d mais d = 1/0 il vient alors 2 = 0*2*1/0 =0/0 et la c'est la porte ouverte à toute les fenêtres :doh:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 16:58
par Dinozzo13 » 05 Mai 2010, 16:58
En effet, ca bousille l'élément neutre.
Qu'est-ce que les quaternions ? Si c'est du niveau sup je risque de ne pas être à la hauteur.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Mai 2010, 17:01
par fatal_error » 05 Mai 2010, 17:01
salut,
de mémoire pour la division par 0, javais eu un exo ou on avait
convention :
a/0 = infini
et on avait une opération qui était pour a et b dans R
a//b = 1/(1/a+1/b)
on avait du montrer que c'était un monoïde ou un autre truc savant dont je retiens jamais les noms.
Ca rappele accessoirement le calcul d'une resistance equivalente pour un circuit en dérivation.
avec les résultats que Req = 0 si une des resistance vaut 0.
Bref, voilà une utilité pour poser a/0=infini
la vie est une fête

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 17:02
par Dinozzo13 » 05 Mai 2010, 17:02
anthony_unac a écrit:Mais alors dans ce cas si d=1/0 "alors" 1=d*0 or 1 ne peut pas être égal à zéro puisque 1 est le succésseur de zéro.
Je poursuis encore :
2*d = 2*1/0 = 2/0 "donc" 2 = 0*2*d mais d = 1/0 il vient alors 2 = 0*2*1/0 =0/0 et la c'est la porte ouverte à toute les fenêtres :doh:
C'est là qu'on se dit que si on change ou considère quelque chose.
Néanmoins, cette etude de remplacement de 1/0 par une lettre a-t-elle déjà faite ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 17:07
par Dinozzo13 » 05 Mai 2010, 17:07
fatal_error a écrit:salut,
de mémoire pour la division par 0, javais eu un exo ou on avait
convention :
a/0 = infini
et on avait une opération qui était pour a et b dans R
a//b = 1/(1/a+1/b)
on avait du montrer que c'était un monoïde ou un autre truc savant dont je retiens jamais les noms.
Ca rappele accessoirement le calcul d'une resistance equivalente pour un circuit en dérivation.
avec les résultats que Req = 0 si une des resistance vaut 0.
Bref, voilà une utilité pour poser a/0=infini
Quand tu dis

, pourquoi ne mets-tu pas un + ou un - ? Car je ne vois pas bien ce que signifie \infty sans signe ?
De plus, aurait-on
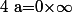
et

?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 17:10
par Dinozzo13 » 05 Mai 2010, 17:10
Ericovitchi a écrit:le problème de poser d=1/0 c'est que ça bousille la notion d'élément neutre 0 dans le corps des réels puisque ça entraîne d fois 0 = 1 qui est contraire à la définition d'un élément neutre pour la multiplication.
Donc ça n'a plus une structure de corps. Il faudrait trouver un nouvel élément neutre, ou une nouvelle opération remplaçant la multiplication (commutative, distributive sur l'addition, etc, etc... ).
Donc ça ne va pas, ça ne laisse pas intègre les définitions des opérations.
tu devrais t'intéresser aux quaternions plutôt, si tu veux jouer au chercheur de nouvelles structures.
Mais alors comment on-t-il fait pour les nombres complexes avec
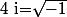
pour satisfaire toutes ces conditions ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Mai 2010, 17:11
par fatal_error » 05 Mai 2010, 17:11
ben vu qu'on a pas redefini l'opérateur d'égalité, a priori on a
pour tout a dans R a/0=+infini <=> a = 0*infini
vu qu'on peut quand même multiplier par 0, et que diviser par 0 respecte notre convention :)
Apres, si t'arrives a faire capoter, ben t'auras trouvé une limite au modele (si on peut appeler ca un modele).
la vie est une fête

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 17:13
par Dinozzo13 » 05 Mai 2010, 17:13
Qu'est-ce que t'entends par faire capoter ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Mai 2010, 17:15
par fatal_error » 05 Mai 2010, 17:15
ya aucun intéret a avoir
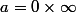
si a c'est la valeur d'une résistance...
+infini, ui, ps : a et b sont positives
la vie est une fête

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Mai 2010, 17:23
par benekire2 » 05 Mai 2010, 17:23
moi je dirais plutôt que c'est libre a toi de définir la division par 0 ; cependant avec les ensembles que tu vas construire avec, tu pourra rien faire de ce que on à l'habitude de faire ... en fait ça sert a rien ...
enfin pour les quaternions regarde là :
http://fr.wikipedia.org/wiki/Quaternion
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 05 Mai 2010, 17:33
par Arnaud-29-31 » 05 Mai 2010, 17:33
Il te faut le programme de sup pour voir comment les corps sont construits et voir que ceci ne peut avoir de sens ...
Attention, lorsque tu écris
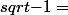
i ... ce n'est pas parce qu'on a les complexes qu'on a le droit de mettre un nombre négatif sous une racine, contrairement a ce que dit ton topic, les racines carrées d'un nombre négatif n'existent pas. Racine carré reste une fonction de
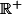
dans
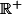
...
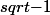
ca n'a toujours pas de sens.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Mai 2010, 17:36
par Nightmare » 05 Mai 2010, 17:36
Salut !
La notion de division par 0 n'a pas de sens car 0 n'est jamais inversible. Par contre, la notion de "diviseurs de 0" existe bel est bien. Dans C (dans tout corps de manière général) on sait que pour qu'un produit fasse 0, il faut nécessairement qu'un des facteurs soit nul. Si l'on raisonne par exemple sur les classes de reste modulo un entier n, le produit par exemple 4*5 est nul modulo 10 sans qu'aucun des deux facteurs ne le soit. Cependant, on ne peut pas écrire que 4/0 = 5 puisqu'on a aussi 4*15=0 mod 10 et plus simplement 4*0 = 0 [10]. Qu'écrire alors? 4/0 =5 ? 4/0 = 15 ? 4/0=0 ? On ne peut rien décider.
-
Hir
- Membre Relatif
- Messages: 120
- Enregistré le: 07 Déc 2008, 15:43
-
 par Hir » 05 Mai 2010, 18:13
par Hir » 05 Mai 2010, 18:13
Nightmare a écrit: Par contre, la notion de "diviseurs de 0" existe bel est bien. Dans C (dans tout corps de manière général) on sait que pour qu'un produit fasse 0, il faut nécessairement qu'un des facteurs soit nul. Si l'on raisonne par exemple sur les classes de reste modulo un entier n, le produit par exemple 4*5 est nul modulo 10 sans qu'aucun des deux facteurs ne le soit.
De même on peut trouver, dans l'ensemble des fonctions à valeurs réelles, 2 fonctions f et g (qui ne soient pas la fonction nulle) telles que le produit (f*g) soit nul.
Et pour revenir à ta proposition de définition, Dinozzo, il faut quand même se poser un peu la question de l'utilité d'une telle "invention". Les nombres complexes par exemple permettent de résoudre des problèmes d'électrocinétique et de mécanique, entre autres...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 19:29
par Dinozzo13 » 05 Mai 2010, 19:29
Ok, merci bien pour toutes ces questions enrichissante, je suis satisfait :+++:
Par contre l'histoire des quaternions, j'ai pas bien pigé :cry:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 05 Mai 2010, 19:36
par Arnaud-29-31 » 05 Mai 2010, 19:36
En très très gros, le corps des quaternions à été construit via une extension des nombres complexes.
De la même façon que l'on a étendu l'ensemble des réels en l'ensemble des complexes pour décrire le plan, on a étendu l'ensemble des complexes en l'ensemble des quaternions pour décrire l'espace ...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Mai 2010, 19:53
par Dinozzo13 » 05 Mai 2010, 19:53
Ah ok, donc
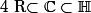
?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 05 Mai 2010, 20:14
par Arnaud-29-31 » 05 Mai 2010, 20:14
Affirm ...

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 09 Mai 2010, 19:38
par Lostounet » 09 Mai 2010, 19:38
On en aura peut-être besoin, un jour?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
