Bonjour,
Est il possible de se représenter un objet géométrique, par exemple un triangle rectangle, dont la longueur des côtés sont des nombres complexes ?
Par exemple un triangle rectangle en A dont AB=6+3i et AC=8+5i
Si je ne me suis pas trompé dans mes calculs, en prenant la formule conventionnelle AC devrait mesurer approximativement 10,24 + 6,24i
Merci.
Géométrie et nombres complexes.
12 messages
- Page 1 sur 1
Re: Géométrie et nombres complexes.
Bonjour,
1) tout d'abord, pourrais-tu nous dire ce que tu entends par
2) à quoi est égal le module d'un nombre complexe?
1) tout d'abord, pourrais-tu nous dire ce que tu entends par
en prenant la formule conventionnelle AC...
2) à quoi est égal le module d'un nombre complexe?
Re: Géométrie et nombres complexes.
1/ la formule pour calculer l’hypoténuse d'un triangle rectangle, BC²=AB²+AC²
2/racine carré de la somme de la partie réelle et imaginaire du nombre complexe
2/racine carré de la somme de la partie réelle et imaginaire du nombre complexe
Re: Géométrie et nombres complexes.
Bonjour,
soient A et B deux points du plan (le plan muni d'un repère orthonormé) de coordonnées
) et
et )
le vecteur a pour coordonnées
a pour coordonnées ) . le vecteur
. le vecteur  a pour affixe
a pour affixe
+i(y_B-y_A)) , avec
, avec 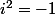 . Si tu veux, l'affixe d'un vecteur est sa coordonnée complexe.
. Si tu veux, l'affixe d'un vecteur est sa coordonnée complexe.
Dans ces conditions, un vecteur a une norme (sa longueur) , notée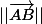 .
.
on a=AB=||\vec{AB}|| = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2})
d(A,B) est la distance (euclidienne) du point A au point B.
une norme est une application du plan vectoriel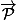 dans
dans 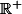
Une norme doit vérifier trois propriétés:
 et
et  sont des vecteurs du plan:
sont des vecteurs du plan:
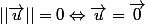

pour réel,
réel, 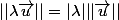
soient A et B deux points du plan (le plan muni d'un repère orthonormé) de coordonnées
le vecteur
Dans ces conditions, un vecteur a une norme (sa longueur) , notée
on a
d(A,B) est la distance (euclidienne) du point A au point B.
une norme est une application du plan vectoriel
Une norme doit vérifier trois propriétés:
pour
Modifié en dernier par mathelot le 23 Nov 2022, 11:25, modifié 1 fois.
Re: Géométrie et nombres complexes.
@Frederic87
puisque mathelot t'as donné toutes les infos je m'éclipse
je m'éclipse
puisque mathelot t'as donné toutes les infos
Re: Géométrie et nombres complexes.
Pisigma a écrit:@Frederic87
puisque mathelot t'as donné toutes les infosje m'éclipse
@Pisigma , bah non ,reste , j'ai écrit quelques formules mais il manque la mise en pratique
Re: Géométrie et nombres complexes.
Ok merci, il faut que je me pose pour étudier ça, je reviens plus tard si j'ai encore des questionnements  .
.
Re: Géométrie et nombres complexes.
Tout ça me surprend beaucoup.
D'où vient l'énoncé, quel est l'énoncé précis ?
Un triangle dont les cotés sont AB=6+3i et AC=8+5i : ok, pourquoi pas.
Mais quand tu dis : la longueur des côtés sont des nombres complexes ?
Bof bof bof ...
Et tu dis que ce triangle serait rectangle en A.
Ca ne me paraît pas compatible avec les informations AB=6+3i et AC=8+5i
Si on avait par exemple AB=6+i et AC=-1+6i , ok, je dirais qu'il y a des trucs bizarres, mais passons.
Là, c'est très très louche.
D'où vient l'énoncé, quel est l'énoncé précis ?
Un triangle dont les cotés sont AB=6+3i et AC=8+5i : ok, pourquoi pas.
Mais quand tu dis : la longueur des côtés sont des nombres complexes ?
Bof bof bof ...
Et tu dis que ce triangle serait rectangle en A.
Ca ne me paraît pas compatible avec les informations AB=6+3i et AC=8+5i
Si on avait par exemple AB=6+i et AC=-1+6i , ok, je dirais qu'il y a des trucs bizarres, mais passons.
Là, c'est très très louche.
Re: Géométrie et nombres complexes.
Bonjour,
Oui c'est louche en effet, ma question n'était pas de pouvoir tracer un triangle rectangle sur le plan complexe mais bien de visualiser un triangle rectangle dont la longueur des côtés seraient des nombres complexes.
ça peut effectivement ne pas avoir de sens, mais je voulais savoir si des mathématiciens s'était déjà posé la question et si il y avait un début de réponse à cette question. Merci.
Oui c'est louche en effet, ma question n'était pas de pouvoir tracer un triangle rectangle sur le plan complexe mais bien de visualiser un triangle rectangle dont la longueur des côtés seraient des nombres complexes.
ça peut effectivement ne pas avoir de sens, mais je voulais savoir si des mathématiciens s'était déjà posé la question et si il y avait un début de réponse à cette question. Merci.
Re: Géométrie et nombres complexes.
Une longueur est un nombre réel positif.
Sont donc exclus les réels négatifs et les complexes autres que les réels positifs.
Sont donc exclus les réels négatifs et les complexes autres que les réels positifs.
Re: Géométrie et nombres complexes.
Bonjour,
Soit ABC un triangle rectangle en A.
a,b,c,d,e,f sont réels.
On considère les affixes des vecteurs
, \vec{AC}(c+id),\vec{BC}(e+if)) avec
avec 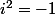
L'égalité de Pythagore (BC est l'hypoténuse) s'écrit:

soit:
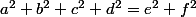
on remarque qu'il n'y a plus de "i" dans l'égalité, et que c'est une égalité entre nombres réels positifs.
Soit ABC un triangle rectangle en A.
a,b,c,d,e,f sont réels.
On considère les affixes des vecteurs
L'égalité de Pythagore (BC est l'hypoténuse) s'écrit:
soit:
on remarque qu'il n'y a plus de "i" dans l'égalité, et que c'est une égalité entre nombres réels positifs.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
