Nombres complexes - Méthode pédagogique

[busard_des_roseaux]

salut,


je souhaite expliquer les nombres complexes à mimi (elle est en Seconde).
Comme elle connait les coordonnées et la trigonométrie de seconde, je pense que ça devrait pouvoir passer.

Juste une question:
pour montrer
est-ce que j'ai besoin des formules d'addition du style

cos(a+b)=cos(a)cos(b)-sin(a)sin(b)

formule qui s'obtiennent avec le produit scalaire de la classe de Première
(en France) ?

est-ce un souci de ne pas avoir la relation de Chasles sur les angles orientés ?

merci pour vos conseils.

[phryte]

Bonjour

pour montrer e^{i(\theta+\theta')}=e^{i \theta} e^{i theta'}

Il suffit qu'elle ait compris :
x^(a+b) = x^a * x^b

[axiome]

Bonjour

Il suffit qu'elle ait compris :
x^(a+b) = x^a * x^b

Et c'est niveau 4e, donc ça doit passer sans problème.
:++:

[maturin]

oui enfin en 4eme c'est avec a et b réel.
et il me semble qu'on démontre que ça marche aussi avec des complexes en passant justement par cos(a+b) et sin(a+b).
ptêtre je me gourre ça remonte à longtemps mes études :(

[phryte]

ça marche aussi avec des complexes en passant justement par cos(a+b) et sin(a+b).

Je pense que tu confonds avec Moivre.

[Kah]

je souhaite expliquer les nombres complexes à mimi (elle est en Seconde).
Comme elle connait les coordonnées et la trigonométrie de seconde, je pense que ça devrait pouvoir passer.

Et bien bonne chance. Heu par contre, dans ton expression, tu as une exponentielle, qui est une part entiere du programme de Tle.
Dur a expliquer a un(e) seconde.

[Sve@r]

oui enfin en 4eme c'est avec a et b réel.
et il me semble qu'on démontre que ça marche aussi avec des complexes en passant justement par cos(a+b) et sin(a+b).
ptêtre je me gourre ça remonte à longtemps mes études

Pour expliquer les complexes, suffit de poser i²=(-1) et tout part de là. Ensuite, les règles de distributivité, de développement, de réduction restent les mêmes. Mais chaque fois qu'on tombe sur i², on l'enlève et on inverse le signe

Maintenant, pour expliquer pourquoi i²=(-1) au mépris des règles de multiplication enseignées depuis le primaire, c'est plus difficile. A toi de trouver les bon mots...

[Luc]

Pour expliquer les complexes, suffit de poser i²=(-1) et tout part de là. Ensuite, les règles de distributivité, de développement, de réduction restent les mêmes. Mais chaque fois qu'on tombe sur i², on l'enlève et on inverse le signe

Maintenant, pour expliquer pourquoi i²=(-1) au mépris des règles de multiplication enseignées depuis le primaire, c'est plus difficile. A toi de trouver les bon mots...

Je ne suis pas vraiment convaincu de la pertinence pédagogique de cette approche qui est certes exacte, mais qui ne signifie pas grand chose à part que "ça marche". Je préfère expliquer au départ qu'un nombre complexe est un vecteur du plan. Puis qu'on peut le munir d'une structure de corps en interprétant la multiplication comme une similitude directe de centre O.

Sinon, on peut aussi le définir (plus rigoureusement) comme l'ensemble des racines de , ie la clôture algébrique de .


Luc

[Monsieur23]

Je préfère expliquer au départ qu'un nombre complexe est un vecteur du plan. Puis qu'on peut le munir d'une structure de corps en interprétant la multiplication comme une similitude directe de centre O.

Sinon, on peut aussi le définir (plus rigoureusement) comme l'ensemble des racines de \mathbb{R}[X] , ie la clôture algébrique de \mathbb_{R} .

Tellement plus simple à expliquer à quelqu'un en seconde ...

[Timothé Lefebvre]

Salut à tous,

je suis en seconde et j'ai vu les complexes il y a un petit moment, je vais essayer de t'expliquer comment j'ai fait pour le début.

Tout d'abord j'ai commencé par tenter de résoudre cette équation (c'est accessible avec des outils de troisième, très simple).



Je factorise par



Puis par



[Produit de facteurs nul] De là on remarque qu'il y a une solution réelle qui est 1, puis une autre qui semble bizarre qui est

J'explique ensuite que cette deuxième solution appartient à , et qu'elle en est le principal élément noté .

Un autre exemple :

Deux solutions dans qui sont i et -i .

Voilà pour l'introduction, c'est compréhensible par tous, pas besoin d'être en TS.

Pour la suite tu peux dire ce que les autres t'ont dit, c'est à dire le cours complet, ce ne sont pas non plus des notions très dures.

Voilà voilà !

A+

[Sve@r]

Je ne suis pas vraiment convaincu de la pertinence pédagogique de cette approche qui est certes exacte, mais qui ne signifie pas grand chose à part que "ça marche". Je préfère expliquer au départ qu'un nombre complexe est un vecteur du plan. Puis qu'on peut le munir d'une structure de corps en interprétant la multiplication comme une similitude directe de centre O.

Sinon, on peut aussi le définir (plus rigoureusement) comme l'ensemble des racines de , ie la clôture algébrique de .


Luc

Hum... ce genre de discussion (qui peut être passionnant et c'est pourquoi je l'ai déplacé dans la rubrique destinée aux discussions) possède deux points principaux
1) comment expliquer le nombre complexe (qui peut être aussi difficile à appréhender pour certains de nos contemporains que ce que l'était le nombre irrationnel pour Pythagore)
2) quelle méthode pédagogique utiliser

Bon, pour le point 1, je ne peux rien dire. Je le comprends d'une certaine façon et je tente de l'expliquer de la même façon. Peut-être puis-je juste ajouter que cet outil a été inventé au XVIII° siècle pour résoudre une équation du 3° degré et que grace à lui, les solutions réelles de l'équation ont pu être trouvées.

Pour le point 2, ça dépend évidemment de l'interlocuteur. Peut-être que la notion de vecteurs et de similitude de corps n'est pas non-plus adaptée à un lycéen. Je voudrais rebondir à ce sujet sur un livre de Marco Wolf "La bosse des maths est-elle une maladie mentale" (1984, ISBN 2707114650) qui a développé dans son livre avec beaucoup d'humour les inconvénients de la méthode ensembliste pronée dans les années 1970 pour enseigner les mathématiques aux pauvres collégiens de l'époque. Mais bon, de toute façon il n'y a pas de méthode magique. Je reste cependant persuadé que pour expliquer une notion, il faut commencer par des exemples de la vie réelle et la façon dont ils peuvent être schématisés par les mathématiques. Mais évidemment, trouver des exemples de nombres complexes dans la vie réelle.... :briques:

[axiome]

Salut à tous,

je suis en seconde et j'ai vu les complexes il y a un petit moment, je vais essayer de t'expliquer comment j'ai fait pour le début.

Tout d'abord j'ai commencé par tenter de résoudre cette équation (c'est accessible avec des outils de troisième, très simple).



Je factorise par



Puis par



[Produit de facteurs nul] De là on remarque qu'il y a une solution réelle qui est 1, puis une autre qui semble bizarre qui est

J'explique ensuite que cette deuxième solution appartien à , et qu'elle en est le principal élément noté .

Un autre exemple :

Deux solutions dans qui sont i et -i .

Voilà pour l'introduction, c'est compréhensible par tous, pas besoin d'être en TS.

Pour la suite tu peux dire ce que les autres t'ont dit, c'est à dire le cours complet, ce ne sont pas non plus des notions très dures.

Voilà voilà !

A+

Tu te compliques la vie quand même dans ton premier exemple... :happy2:
Sinon, je suis d'accord avec toi, les complexes, c'est pas une notion très compliquée. On les étudie je crois d'ailleurs en première dans certaines filières.

[Timothé Lefebvre]

Hum je crois pas pour la première, en tout cas dans mes bouquins c'est TS.

Le premier exemple c'est une première approche, pour montrer qu'il existe des nombres qui choquent au premier abord, et que toute solution d'une équatio ndn'est pas forcément réelle.

Juste après ça j'explique la formatio nd'un nombre comlexe, de la forme z = a + ib, avec a et b des réels, a la partie relle et ib la partie imaginaire. On peut parler des nombres de la forme z = bi : les imaginaires purs.
Là non plus c'est pas dur.

Après, là où ça se complique c'est à la représentation géométrique du nombre complexe et faire comprendre la notion d'affixe d'un point ...

[axiome]

Ca s'étudie en première STI je crois...

[Timothé Lefebvre]

Serieux ?!

Je l'ignorais totalement, il me semblait que mon prof m'avait dit que c'était uniquement TS ...

Prise de renseignement faite : oui en STI en électricité c'est ça ?

[le_fabien]

Serieux ?!

Je l'ignorais totalement, il me semblait que mon prof m'avait dit que c'était uniquement TS ...

Prise de renseignement faite : oui en STI en électricité c'est ça ?

Et non en STI dès la première, oui oui . :zen:

[axiome]

Serieux ?!

Je l'ignorais totalement, il me semblait que mon prof m'avait dit que c'était uniquement TS ...

Prise de renseignement faite : oui en STI en électricité c'est ça ?

Je crois qu'on trouve des applications en électronique avec les complexes, c'est pour ça, qu'on les étudie en première STI.

[Luc]

Hum... ce genre de discussion (qui peut être passionnant et c'est pourquoi je l'ai déplacé dans la rubrique destinée aux discussions) possède deux points principaux
1) comment expliquer le nombre complexe (qui peut être aussi difficile à appréhender pour certains de nos contemporains que ce que l'était le nombre irrationnel pour Pythagore)
2) quelle méthode pédagogique utiliser

Bon, pour le point 1, je ne peux rien dire. Je le comprends d'une certaine façon et je tente de l'expliquer de la même façon. Peut-être puis-je juste ajouter que cet outil a été inventé au XVIII° siècle pour résoudre une équation du 3° degré et que grace à lui, les solutions réelles de l'équation ont pu être trouvées.

Pour le point 2, ça dépend évidemment de l'interlocuteur. Peut-être que la notion de vecteurs et de similitude de corps n'est pas non-plus adaptée à un lycéen. Je voudrais rebondir à ce sujet sur un livre de Marco Wolf "La bosse des maths est-elle une maladie mentale" (1984, ISBN 2707114650) qui a développé dans son livre avec beaucoup d'humour les inconvénients de la méthode ensembliste pronée dans les années 1970 pour enseigner les mathématiques aux pauvres collégiens de l'époque. Mais bon, de toute façon il n'y a pas de méthode magique. Je reste cependant persuadé que pour expliquer une notion, il faut commencer par des exemples de la vie réelle et la façon dont ils peuvent être schématisés par les mathématiques. Mais évidemment, trouver des exemples de nombres complexes dans la vie réelle.... :briques:

Argh! Je me suis mal fait comprendre. :id:

A mon avis, il ne faut surtout pas expliquer les nombres complexes comme "la clôture algébrique de " à un seconde alors qu'il commence à peine à savoir ce qu'est un polynôme! Ça serait beaucoup trop long et abstrait à expliquer! Je suis d'accord avec toi qu'il vaut mieux

commencer par des exemples de la vie réelle et la façon dont ils peuvent être schématisés par les mathématiques.

Ce que je dis, c'est que ça me parait plus simple, pour un élève de seconde, de voir un nombre complexe comme un élément de (Il connait les vecteurs). Ce qui est magique, c'est qu'on peut munir d'une structure de corps! Effectivement ça c'est moins évident à expliquer, mais on peut interpréter géométriquement la multiplication comme je l'ai déja évoqué. Il ne paraît alors pas impossible qu'un carré soit négatif, ce qui amène à une définition naturelle de i.

Bien entendu toutes les approches (algébriques, géométriques) sont possibles à partir d'exemples. L'approche qu'a évoquée Timothé par les équations est intéressante également car elle fait pressentir l'existence des nombres à carré négatif (c'est d'ailleurs l'approche historique).

Cordialement,

Luc

[Timothé Lefebvre]

Ouaip, je te parle de ça parce que c'est comme ça que je les ai appris, ça m'a parut clair et compréhensible par tous dès le niveau de fin de troisième (bon ok à partir de la représentation géométrique du nombre complexe dans le plan mieux vaut avoir fait une 1S).

Néanmoins, si ton élève aime les maths et est curieux il(elle) ne devrait pas y avoir de problème :lol4:

[ffpower]

Hum... ce genre de discussion (qui peut être passionnant et c'est pourquoi je l'ai déplacé dans la rubrique destinée aux discussions) possède deux points principaux
1) comment expliquer le nombre complexe (qui peut être aussi difficile à appréhender pour certains de nos contemporains que ce que l'était le nombre irrationnel pour Pythagore)
2) quelle méthode pédagogique utiliser

Je pense qu'il faudrait aussi ajouter un point 3)
3)interet des nbs complexes

Pour l introduction des nbs complexes,je vous donne une idée pompée sur un mag de vulgarisation.

Bon,il faut pour bien faire qu elle connaisse la résolution générale des équations de degré 2,et le lien avec les problemes du type
a+b=S,ab=P

Regardons le probleme suivant:Trouver a et b tels que
a+b=10
ab=40

Donc c'est parti.L equation correspondante a resoudre est X²-10X+40=0
Le discriminant vaut 10²-4.40=-60.Flute,il est négatif,il n a donc pas de racine carrée et ya donc pas de solutions,c est triste.Mais bon,allez soyons fous,faisons comme si on pouvait prendre la racine carrée,juste pour voir^^
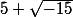
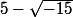
En utilisant la formule classique(avec un discriminant pas classique^^),on obtiens alors les solutions et .Donc on obtiens en effet des nbs qui n existent pas,mais cela dit,si on fait la somme de ces nbres on a ,et si on fais le produit:

Donc nos nombres n existent pas,mais leur somme et leur produit eux,existent et donnent ce que l'on veut...

Donc voila,c est une maniere comme une autre de les introduire,mais cela dit je suis d accord avec Svear:l idée principale et premiere des complexes,c est qu on a une racine carrée de -1,pas de faire de la géométrie^^

Bon,et en ce qui concerne le point 3,trouver une utilité aux complexes,la j ai pas trop d idee:Faudrait trouver un probleme concret,avec une solution concrete mais dont la preuve utilise les complexes comme "intermédiaire".Ya bien la résolution des équations de degré 3,mais ca me semble un peu tendu.Ya aussi la factorisation des poly réels en poly de degré inferieur a 2,mais la ca rejoint l idee de C algebriquement clos,donc c est meme plus de l ordre du faisable.Bon ben je posterai si je trouve une bonne idee alors^^