Fonctions je suis incapable de trouver la reponse
16 messages
- Page 1 sur 1
Fonctions je suis incapable de trouver la reponse
On rappelle qu’une équation de C est donnée par x2 + y2 = 1. Montrez xM est solution del’équation(1+t2)X*2m +2t*2Xm +t*2-1=0.
Quelqu’un pourrai m’aider svpppp
Quelqu’un pourrai m’aider svpppp
Re: Fonctions je suis incapable de trouver la reponse
Bonjour à toi aussi,
énoncé incomplet à revoir
P.S. : x au carré s'écrit x^2
pas envie de jouer aux devinettes!
on attend!
énoncé incomplet à revoir
P.S. : x au carré s'écrit x^2
pas envie de jouer aux devinettes!
on attend!
Re: Fonctions je suis incapable de trouver la reponse
Grnc91 a écrit:On rappelle qu’une équation de C est donnée par x^2+ y^2 = 1. Montrez xM est solution del’équation(1+t^2)X^2m +2t^2Xm +t^2-1=0.
Xm vaut cos(téta)
Quelqu’un pourrai m’aider svpppp
Re: Fonctions je suis incapable de trouver la reponse
2x+2y=1
c'est quoi C?
xM, Xm et X^2m?
Xm vaut cos(téta)??
tout ça n'est pas très clair
c'est quoi C?
xM, Xm et X^2m?
Xm vaut cos(téta)??
tout ça n'est pas très clair
Modifié en dernier par Pisigma le 09 Oct 2021, 17:48, modifié 1 fois.
Re: Fonctions je suis incapable de trouver la reponse
Dans un repère orthonormé, on considère le cercle C de centre l’origine et de rayon 1. Soient A, I et B les points de coordonnées respectives (1,0), (1,0) et (0,t). On note M le point d’interstion de (AB) avec C qui n’est pas sur l’axe de abscisses.
Sa c’est l’énoncer du debut
Sa c’est l’énoncer du debut
Re: Fonctions je suis incapable de trouver la reponse
donc les points A et I sont confondus(même abscisse, même ordonnée)
Re: Fonctions je suis incapable de trouver la reponse
si mais tu dois passer par un hébergeur d'image
Re: Fonctions je suis incapable de trouver la reponse
Dans un repère orthonormé, on considère le cercle C de centre l’origine et de rayon 1. Soient A, I et B les points de coordonnées respectives ( -1,0), (1,0) et (0,t). On note M le point d’interstion de (AB) avec C qui n’est pas sur l’axe de abscisses. . (xM,yM) les coordonées de M.
On rappelle qu’une équation de C est donnée par x^2 + y^2 = 1. Montrez xM est solution de l’équation (1+t2)xM^2 +2t^2xM +t^2 1=0.
J'espère que c'est plus clair maintenant
On rappelle qu’une équation de C est donnée par x^2 + y^2 = 1. Montrez xM est solution de l’équation (1+t2)xM^2 +2t^2xM +t^2 1=0.
J'espère que c'est plus clair maintenant
Re: Fonctions je suis incapable de trouver la reponse
nettement mieux!
il faut d'abord écrire l'équation de la droite qui passe par les points A et B
il faut d'abord écrire l'équation de la droite qui passe par les points A et B
Re: Fonctions je suis incapable de trouver la reponse
oui 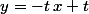
maintenant tu cherches les coordonnées de)
en résolvant le système
& \\ <br />y=-t\,x+t (2) <br />\end{cases})
maintenant tu cherches les coordonnées de
en résolvant le système
Modifié en dernier par Pisigma le 09 Oct 2021, 19:34, modifié 1 fois.
Re: Fonctions je suis incapable de trouver la reponse
Ok merci beaucoup je vais essaye et une fois que j’ai trouver je remplace les xm dans l’équation par le xm que j’ai trouvé?
Re: Fonctions je suis incapable de trouver la reponse
en fait on ne te demande pas 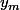 mais on demande uniquement de trouver l'équation
mais on demande uniquement de trouver l'équation
x^2-2xt^2+t^2-1=0) ensuite il suffit de remplacer
ensuite il suffit de remplacer  par
par 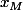
Re: Fonctions je suis incapable de trouver la reponse
L’équation je la trouve en résolvant le système?
Re: Fonctions je suis incapable de trouver la reponse
tu mets (2) dans (1) et tu auras "ton" expression
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
