Salut,
Le truc, c'est que ce n'est pas du tout
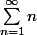
qui vaut -1/12 (en ce moment, ça fait visiblement fureur sur le net de présenter ça sous cette forme débile....)
La fonction zéta, on peut la définir
pour les complexes s de partie réelle >1 comme étant égale à
=\sum_{n\geq 1}\frac{1}{n^s})
.
Pour de tels s, la série est convergente et ç'est donc on ne peut plus cohérent.
Après, le truc, c'est que la fonction ainsi définie peut
se prolonger de façon analytique au plan complexe tout entier privé seulement de 0. Et c'est ce prolongement qui prend la valeur -1/12 en s=-1.
Fondamentalement, écrire que
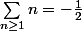
, c'est la même chose que d'écrire que
-1}{0^2}=-\frac{1}{2})
sous prétexte que la fonction
-1}{x^2})
se prolonge en x=0 avec la valeur -1/2 : c'est clairement un énorme abus de notation à proscrire impérativement si on ne veut pas finir par écrire n'importe quoi...
