Exo de logique + B..

[nada-top]

ni hao :lol3:

exo :

vérifier la véracité de cette proposition :

E un ensemble fini et card(E)=n '' il exsite une application surjective de E ''

Bonnus : soient et
prouver l'existence du couple tel que :

indice : quelques simples principes peuvent être parfois trés utiles .:lol4:

good luck :lol3:

[alben]

E un ensemble fini et card(E)=n '' il exsite une application surjective de E ''

pas vrai : principe des tiroirs .

Bonnus : soient et
prouver l'existence du couple tel que :

Il manque la condition

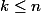
[nada-top]

pas vrai : principe des tiroirs .

c bon ..mais le lemme des bergers me parait plus adéquat non?:lol4:

sinon pour le bonnus je ne me rappelle pas t bien de l'énoncé mais je peux t'affirmer que ces conditions sont trés suffisantes pour prouver l'existence de (m,k) :lol3:

zu ni hao yen :lol3:

[Roman]

Bonjour,

D'ailleurs, nada-top, l'enonce de ton exercice reste faux meme si tu ne supposes plus que E est un ensemble fini !

Exo:

Le demontrer (c'est un classique de theorie des ensembles, mais plus de tiroirs ni de bergers lorsque l'ensemble est infini...)

Roman

[nada-top]

Bonjour,

E un ensemble fini et card(E)=n '' il exsite une application surjective de E ''

ça suffit pas ?!!!