Demontrer exp(0)=1
32 messages
- Page 1 sur 2 - 1, 2
C'est sûr que cela dépend de la définition que l'on se donne à la base pour l'exponentielle.
Contrairement au lycée, où on nous l'avait introduit de la manière d'Euler911, en prépa on nous a affirmé qu'elle avait été introduite dans un premier temps comme la réciproque du logarithme.
Après, quoi qu'il arrive on arrive aux mêmes choses ^^
Contrairement au lycée, où on nous l'avait introduit de la manière d'Euler911, en prépa on nous a affirmé qu'elle avait été introduite dans un premier temps comme la réciproque du logarithme.
Après, quoi qu'il arrive on arrive aux mêmes choses ^^
Bonsoir
Il me semble qu'il n'a pas été dit ceci, qui serait tout aussi judicieux: "exponentielle" est un adjectif en rapport avec le nom "exposant". Les fonctions exponentielles sont des fonctions de la forme f: x-> a^x, où a est dit la base de cette exponentielle. Or, tout nombre (en particulier, ici, e) élevé à la puissance 0 donne 1
Il me semble qu'il n'a pas été dit ceci, qui serait tout aussi judicieux: "exponentielle" est un adjectif en rapport avec le nom "exposant". Les fonctions exponentielles sont des fonctions de la forme f: x-> a^x, où a est dit la base de cette exponentielle. Or, tout nombre (en particulier, ici, e) élevé à la puissance 0 donne 1
Bastien L. a écrit:Bonsoir
Il me semble qu'il n'a pas été dit ceci, qui serait tout aussi judicieux: "exponentielle" est un adjectif en rapport avec le nom "exposant". Les fonctions exponentielles sont des fonctions de la forme f: x-> a^x, où a est dit la base de cette exponentielle. Or, tout nombre (en particulier, ici, e) élevé à la puissance 0 donne 1
Dans ce cas, démontre nous cette propriété des exposants...
Il n'empêche, il y a un truc qui m'intéresse vivement, c'est l'exponentielle de base 0!
Alors que chacun s'accordera pour la trouver sans intérêt sur \mathbb{R}*, je suis sûr que certains passeraient des nuits à se demander quel est son comportement en 0, ne serait-ce que pour savoir si elle y est définie! :we:
Alors que chacun s'accordera pour la trouver sans intérêt sur \mathbb{R}*, je suis sûr que certains passeraient des nuits à se demander quel est son comportement en 0, ne serait-ce que pour savoir si elle y est définie! :we:
D'après ce que j'ai peu lire l'exponentielle de base 0 n'a que peut d'intérêt...
Son domaine de définition est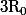 et son domaine image est 0... peu utile! Le seule chose qui pourrait être intéressante est d'étudier ceci :
et son domaine image est 0... peu utile! Le seule chose qui pourrait être intéressante est d'étudier ceci : 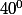
C'est une forme indéterminée, mais pourquoi? Comment? Est-ce que cette indétermination est utile...?
Peut-être...
Son domaine de définition est
C'est une forme indéterminée, mais pourquoi? Comment? Est-ce que cette indétermination est utile...?
Peut-être...
héé l'eau !
la difficulté n'est pas de dire ce que vaut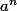 avdc
avdc 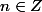 , voire
, voire 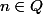 , mais de justifier des propriétés avec des exposants réels, non ?
, mais de justifier des propriétés avec des exposants réels, non ?
Bastien L. a écrit:Ah!
J'avoue que je ne m'étais pas trop posé la question
Sur Wikipédia, on propose ceci: a^0 = a^(1-1) = a/a = 1.
(Désolé pour la mise en forme, je ne me suis pas encore penché sur la façon d'écrire de jolies équations )
la difficulté n'est pas de dire ce que vaut
Concernant 0^0, c'est du gros :id: .
Ya des gens (matheux) qui ont pondu des posts plutot pas mal.
En gros, ya des histoires de conventions mais ya aussi des questions de passages à la limite.
Enfin yavait un truc que j'avais lu assez compliqué (pour moi) avec des espaces vectoriels mais ca doit se retrouver facilement avec google, futura-sciences, pe math forum qui sait :zen:
Ya des gens (matheux) qui ont pondu des posts plutot pas mal.
En gros, ya des histoires de conventions mais ya aussi des questions de passages à la limite.
Enfin yavait un truc que j'avais lu assez compliqué (pour moi) avec des espaces vectoriels mais ca doit se retrouver facilement avec google, futura-sciences, pe math forum qui sait :zen:
la vie est une fête 
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
