Salut à tous,
Existe-t-il une méthode pour définir une fonction sachant que :
f(x)>0 sur R, y=0 asymptôte hrzt.
La courbe possède 2 maxima (en xA, yA et xB, yB) donc aussi un minimum en xC, yC. (xA < xC < xB) Ce qui signifierait que f'(x) a 3 racines, qu'elle soit + de - l'infini à xA, qu'elle soit - de xA à xC, puis + de xC à xB , et enfin - pour la suite.
Toutes indications ou pistes sont bien venues.
En fait c'est pour générer des courbes aléatoires de réflectance colorimétrique (en choisissant xA,et xB et yA et yB) et où 400nm < x < 700 nm et f(x) = R% (0 à 100%) qui est le taux d'énergie ré emise en fonction de la longueur d'onde.
J'espère avoir été clair.
Merci d'avance.
Définir une fonction selon des éléments de sa courbe
12 messages
- Page 1 sur 1
OUaou!!
bon j'ai pas tout compris, mais à mon humble avis tu dois peut etre pouvoir t'en sortir avec la forumle d'interpolation des polynomes de lagrange.
Il te suffit d connaitre les coordonnées de plusieurs points et tu peux générer avec cette formule un polynomequi passe par ces points, plus tu as de points meilleure est donc la fonction approximée.
Voilà si ça t'intéresse je dois pouvoir retrouver cette formule!
bon j'ai pas tout compris, mais à mon humble avis tu dois peut etre pouvoir t'en sortir avec la forumle d'interpolation des polynomes de lagrange.
Il te suffit d connaitre les coordonnées de plusieurs points et tu peux générer avec cette formule un polynomequi passe par ces points, plus tu as de points meilleure est donc la fonction approximée.
Voilà si ça t'intéresse je dois pouvoir retrouver cette formule!
Salut Laurent,
je n'ai pas bien le temps de réfléchir à la question, mais voici quelques précisions :
- C'est une erreur que de penser que plus on a de points, plus l'interpolation polynômiale de Lagrange approxime de façon efficace une fonction passant par les points d'interpolation
- Si on note (xi,yi) les n points à interpoler, on défini li(x) = (produit de j=1 à n , j différent de i, de (x-xj) / (xi - xj). Alors li(xk) = 0 si k différent de i , = 1 si k=i.
On pose p(x) = somme de 0 à n des yi*li(x), qui est alors le polynôme de Lagrange interpolant les (xi,yi).
Mais je crois qu'ici Lagrange ne peut pas servir, à cause notamment des conditions avec les asymptotes.

je n'ai pas bien le temps de réfléchir à la question, mais voici quelques précisions :
- C'est une erreur que de penser que plus on a de points, plus l'interpolation polynômiale de Lagrange approxime de façon efficace une fonction passant par les points d'interpolation
- Si on note (xi,yi) les n points à interpoler, on défini li(x) = (produit de j=1 à n , j différent de i, de (x-xj) / (xi - xj). Alors li(xk) = 0 si k différent de i , = 1 si k=i.
On pose p(x) = somme de 0 à n des yi*li(x), qui est alors le polynôme de Lagrange interpolant les (xi,yi).
Mais je crois qu'ici Lagrange ne peut pas servir, à cause notamment des conditions avec les asymptotes.
En fait les courbes de Béziers comme les splines servent à faire de l'interpolation par des fonctions polynômiales par morceaux de sorte que "l'allure de la courbe" que l'on a échantillonnée (dont on connaît seulement quelques points, par exemple des mesures en physique) varie peu quand on rajoute un point connu.
En chaque point que l'on connaît on fait un raccord C2 (continuité de la dérivée seconde) avec des fonctions polynômiales de degré 3 par morceaux (splines cubiques), C3 avec des fonctions polynômiales de degré 4 par morceaux etc.
Cela reste malheureusement un problème "local", le but de ces courbes étant de lisser un tracé de courbe fini (comme dans un logiciel de dessin vectoriel).
Pour en revenir au problème, il doit exister une solution qui serait une fonction rationnelle, en jouant sur les coefficients et sur le fait que le dénominateur n'a pas de racines, on doit pouvoir trouver une solution.
En chaque point que l'on connaît on fait un raccord C2 (continuité de la dérivée seconde) avec des fonctions polynômiales de degré 3 par morceaux (splines cubiques), C3 avec des fonctions polynômiales de degré 4 par morceaux etc.
Cela reste malheureusement un problème "local", le but de ces courbes étant de lisser un tracé de courbe fini (comme dans un logiciel de dessin vectoriel).
Pour en revenir au problème, il doit exister une solution qui serait une fonction rationnelle, en jouant sur les coefficients et sur le fait que le dénominateur n'a pas de racines, on doit pouvoir trouver une solution.
une solution ?
(sans relecture ni explicitation définitive) :
on considère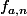 :
: 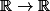
(x-a+1/n)}) si x est dans ]a-1/n, a+1/n[, 0 sinon.
si x est dans ]a-1/n, a+1/n[, 0 sinon.
(f(a,n) est indéfiniment dérivable, elle a un maximum en a qui vaut e^{n^2}).
on prend alors yA*f(xA,n1)/n1^2+yB*f(xB,n2)/n2^2 en ajustant "correctement" n1 et n2 en fonction de yA et yB pour que on ait bien "deux bosses" correspondant aux deux maximums voulus, plutôt qu'une courbe "relativement plate au milieu". En gros plus n1 et n2 sont grands mieux ça marche.
En choisissant n réel positif plutôt qu'entier, on peut même choisir n1 et n2 pour que cette solution ait son minimum local en xC choisi.
Il reste juste à adapter n1 et n2 , ça doit pouvoir se faire algorithmiquement
, ça doit pouvoir se faire algorithmiquement
on considère
(f(a,n) est indéfiniment dérivable, elle a un maximum en a qui vaut e^{n^2}).
on prend alors yA*f(xA,n1)/n1^2+yB*f(xB,n2)/n2^2 en ajustant "correctement" n1 et n2 en fonction de yA et yB pour que on ait bien "deux bosses" correspondant aux deux maximums voulus, plutôt qu'une courbe "relativement plate au milieu". En gros plus n1 et n2 sont grands mieux ça marche.
En choisissant n réel positif plutôt qu'entier, on peut même choisir n1 et n2 pour que cette solution ait son minimum local en xC choisi.
Il reste juste à adapter n1 et n2
merci
Ayant été absent, je n'avais pas pu regarder vos suggestions. mais je suis agréablement surpris de voir que ma question ait pu interesser des gars de votre niveau.
Merci à tous et surtout à khivapia qui semble être le plus proche de ce que j'espérais. (on comprend ce que membre confirmé veut dire....)
Je vais essayer de construire mes courbe avec çà.
Khivapia : peux-tu développer ton idée dans ton 2 ème paragraphe ? (si possible)
Je vous tiendrai au courant
à+
Merci à tous et surtout à khivapia qui semble être le plus proche de ce que j'espérais. (on comprend ce que membre confirmé veut dire....)
Je vais essayer de construire mes courbe avec çà.
Khivapia : peux-tu développer ton idée dans ton 2 ème paragraphe ? (si possible)
Je vous tiendrai au courant
à+
Tout d'abord je tiens à m'excuser, il me semble avoir fait une erreur : le maximum de la fonction f(a,n) me semble plutôt être e^{-n^2}, il faut donc prendre yA*f(xA,n1)*e^{n1^2}+yB*f(xB,n2)*e^{n2^2}
En fait f(a,n) est nulle à l'extérieur de ]a-1/n, a+1/n[. Donc plus n est grand plus cet intervalle est petit, la courbe représentative de f(a,n) se resserre.
Quel en est l'intérêt : tout d'abord, si tu prends n=1 et par exemple (pas tout à fait sûr mais ça doit marcher) xA=-1/50 et xB = 1/50, et yA = yB = 1, la fonction obtenue va avoir un maximum en 0 et non pas en xA et xB, parce que en fait on additionnera deux fonctions bosses trop proches l'une de l'autre :
(regarde avec un logiciel qui trace des courbes tu comprendras mieux) :
/\
/ \
_/ \_
+
/\
/ \
__/ \_____ (légèrement décalée à droite)
=
/\
| |
| |
_| |___ (un seul maximum hélas ; et un peut plus arrondi au milieu)
alors que si les n est grands, fatalement on tombera sur quelque chose comme ça :
|
| |
_| |__
+
|
| |
___| |__
=
| |
| | | |
__| | |__
A la limite, on peut augmenter n1 et n2 jusqu'à ce que les deux bosses soient disjointes, on pourra additionner sans problème.
Le tout c'est que la deuxième fonction ne commence pas à monter avant que la première ait atteint son maximum, sinon on n'a pas de maximum local en xA.
En réglant plus finement n1 par rapport à n2, on peut jouer sur la position du minimum, par exemple n1=n2 impose que le minimum soit au milieu de xA et xB, mais augmenter l'un et pas l'autre décale le minimum). Et pour choisir une position du minimum imposée, on peut prendre n réel positif (non nul).
Voilà, ce n'est pas facile à expliquer sans dessins corrects, si tu as d'autres questions n'hésite pas.
En fait f(a,n) est nulle à l'extérieur de ]a-1/n, a+1/n[. Donc plus n est grand plus cet intervalle est petit, la courbe représentative de f(a,n) se resserre.
Quel en est l'intérêt : tout d'abord, si tu prends n=1 et par exemple (pas tout à fait sûr mais ça doit marcher) xA=-1/50 et xB = 1/50, et yA = yB = 1, la fonction obtenue va avoir un maximum en 0 et non pas en xA et xB, parce que en fait on additionnera deux fonctions bosses trop proches l'une de l'autre :
(regarde avec un logiciel qui trace des courbes tu comprendras mieux) :
/\
/ \
_/ \_
+
/\
/ \
__/ \_____ (légèrement décalée à droite)
=
/\
| |
| |
_| |___ (un seul maximum hélas ; et un peut plus arrondi au milieu)
alors que si les n est grands, fatalement on tombera sur quelque chose comme ça :
|
| |
_| |__
+
|
| |
___| |__
=
| |
| | | |
__| | |__
A la limite, on peut augmenter n1 et n2 jusqu'à ce que les deux bosses soient disjointes, on pourra additionner sans problème.
Le tout c'est que la deuxième fonction ne commence pas à monter avant que la première ait atteint son maximum, sinon on n'a pas de maximum local en xA.
En réglant plus finement n1 par rapport à n2, on peut jouer sur la position du minimum, par exemple n1=n2 impose que le minimum soit au milieu de xA et xB, mais augmenter l'un et pas l'autre décale le minimum). Et pour choisir une position du minimum imposée, on peut prendre n réel positif (non nul).
Voilà, ce n'est pas facile à expliquer sans dessins corrects, si tu as d'autres questions n'hésite pas.
Questions subsidiaires
Pour répondre aux contraintes de F(x)>0 et d'asymptote y=o en + et - l'infini il est impératif d'utiliser l'inverse d'un fonction exponentielle de degré paire.
On utilise 2 fonctions f(x) et g(x) du type = k/e^((x/b)+a)^(2n)
(desolé mais je ne sais pas utiliser l'éditeur d'équation s'il y en a un)
où
k donne le maxi (yA pour f et yB pour g)
a donne le décalage sur abscisses (à droite si 0)
b contrôle la dilatation de la base de la courbe en cloche.
Finalement il y a deux approches pour tracer une courbe de ce type avec 2 "bosses" A et B et un minima C au centre.
La plus simple est de faire la somme de deux fonctions du type ci dessus (merci khivapia). La précaution à prendre pour avoir un "creux" entre A et B est que l'abscisse du point d'inflexion de la branche gauche de B soit > à l'abscisse du point d'inflexion de la branche droite de A (quand le sommet A est à gauche). Les points d'inflexion sont donnés par la dérivée seconde qui s'annule.Dans cette approche la valeur du minimum C est une conséquence des coordonnées définies pour A et B. Ce n'est déjà pas si mal.
La plus complexe serait d'imposer les coordonnées des 3 points A, B et C. C'est probablement faisable mais ça se complique sérieusement. Il faudrait pouvoir définir le minimum C en fonction des coordonnées du point d''intersection des courbes (f=g) car évidemment ces 2 points sont différents. De là on défini f puis g. A vérifier si on a du temps à perdre mais ce doit être "marrant'.
J'aurais bien aimé illustrer mes dires mais il n'y ait pas moyen de mettre des graphes en pièces jointes sur ce site. (un petit dessin vaut mieux qu'un grand discours).
Dites moi au moins comment vous faites pour utiliser un éditeur d'équation ?
Salut à tous et merci.
On utilise 2 fonctions f(x) et g(x) du type = k/e^((x/b)+a)^(2n)
(desolé mais je ne sais pas utiliser l'éditeur d'équation s'il y en a un)
où
k donne le maxi (yA pour f et yB pour g)
a donne le décalage sur abscisses (à droite si 0)
b contrôle la dilatation de la base de la courbe en cloche.
Finalement il y a deux approches pour tracer une courbe de ce type avec 2 "bosses" A et B et un minima C au centre.
La plus simple est de faire la somme de deux fonctions du type ci dessus (merci khivapia). La précaution à prendre pour avoir un "creux" entre A et B est que l'abscisse du point d'inflexion de la branche gauche de B soit > à l'abscisse du point d'inflexion de la branche droite de A (quand le sommet A est à gauche). Les points d'inflexion sont donnés par la dérivée seconde qui s'annule.Dans cette approche la valeur du minimum C est une conséquence des coordonnées définies pour A et B. Ce n'est déjà pas si mal.
La plus complexe serait d'imposer les coordonnées des 3 points A, B et C. C'est probablement faisable mais ça se complique sérieusement. Il faudrait pouvoir définir le minimum C en fonction des coordonnées du point d''intersection des courbes (f=g) car évidemment ces 2 points sont différents. De là on défini f puis g. A vérifier si on a du temps à perdre mais ce doit être "marrant'.
J'aurais bien aimé illustrer mes dires mais il n'y ait pas moyen de mettre des graphes en pièces jointes sur ce site. (un petit dessin vaut mieux qu'un grand discours).
Dites moi au moins comment vous faites pour utiliser un éditeur d'équation ?
Salut à tous et merci.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
