Définir la constante Lipschitz de la fonction f(x)=-b(x^2)
18 messages
- Page 1 sur 1
Définir la constante Lipschitz de la fonction f(x)=-b(x^2)
Bonjour à toute la communauté,
Pour des fins de calcul de loi de commande, j'ai besoin de bien définir la constante Lipschitz d'une fonction non linéaire,
la fonction en question est : f(x)=-0.1*(x^2), et cela dans un intervalle x compris entre [0,50], et j'aimerai bien savoir comment y procéder !
Merci d'avance !
Pour des fins de calcul de loi de commande, j'ai besoin de bien définir la constante Lipschitz d'une fonction non linéaire,
la fonction en question est : f(x)=-0.1*(x^2), et cela dans un intervalle x compris entre [0,50], et j'aimerai bien savoir comment y procéder !
Merci d'avance !
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Quelle est la définition d'une constante de Lipschitz associée à une fonction ?
Un petit tour sur wikipédia ne m'a pas vraiment aiguillé ?
Un petit tour sur wikipédia ne m'a pas vraiment aiguillé ?
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Bonjour,
En somme, pour x[a,b], |f(x2)-f(x1)|<= L|x2-x1| tel que L>0 est la constante de Lipschitz !
En somme, pour x[a,b], |f(x2)-f(x1)|<= L|x2-x1| tel que L>0 est la constante de Lipschitz !
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Et cette constante est unique à chaque fois ?!
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Pour le même intervalle ! normalement oui !
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Et cette constante unique est toujours existante quelque soit la fonction ?
Si mettons (prenons un cas simple), je cherche la dite constante en travaillant dans l'intervalle
en travaillant dans l'intervalle  associée à la fonction
associée à la fonction 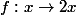
Que peut on dire de plus que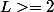 si on suit la définition que vous m'avez donné ?
si on suit la définition que vous m'avez donné ?
Si mettons (prenons un cas simple), je cherche la dite constante
Que peut on dire de plus que
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Oui là c'est clair, mais si la pente était négative(f(x)=-2x) est-ce que je pourrai dire que L=-2, sachant que par la définition que j'ai trouver le L doit être positif !!!
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Bonjour,
Il y a forcément un ou des éléments faux dans ce que nous avons écrit.
Soit
1/ La définition est incomplète et/ou inexacte
2/ K n'est pas défini pour toutes les fonctions
PS: A la question : "K est il toujours unique ?" Il est faux de répondre oui si celui ci est défini par une inégalité. Ainsi dans mon exemple K appartient à l'intervalle [2;+inf]
Il y a forcément un ou des éléments faux dans ce que nous avons écrit.
Soit
1/ La définition est incomplète et/ou inexacte
2/ K n'est pas défini pour toutes les fonctions
PS: A la question : "K est il toujours unique ?" Il est faux de répondre oui si celui ci est défini par une inégalité. Ainsi dans mon exemple K appartient à l'intervalle [2;+inf]
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Voici la définition :
http://www.math-info.univ-paris5.fr/~av ... ode15.html
On voit bien que dans cette dernière k est dans R^+, donc k>0.
http://www.math-info.univ-paris5.fr/~av ... ode15.html
On voit bien que dans cette dernière k est dans R^+, donc k>0.
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Re,
Après lecture de votre document, il est clair que n'est pas unique.
n'est pas unique.
Concernant votre fonction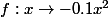
J'obtiens pour tous les couples) de l'intervalle
de l'intervalle 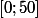
-f(y)|=|-0.1x^2-(-0.1y^2)|=|0.1(y^2-x^2)|)
Si>0 :alors |f(x)-f(y)|=0.1(y^2-x^2))
Si<0 :alors |f(x)-f(y)|=0.1(x^2-y^2))
Vous reconnaissez alors des identités remarquables connus et vous pouvez facilement conclure
Après lecture de votre document, il est clair que
Concernant votre fonction
J'obtiens pour tous les couples
Si
Si
Vous reconnaissez alors des identités remarquables connus et vous pouvez facilement conclure
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
@anthony_unac
Il vaut mieux éviter d'utiliser pour un abscisse.
pour un abscisse.
Il vaut mieux éviter d'utiliser
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Salut,
donc :
f(x2)-f(x1)=-bx2^2+bx1^2
=b[x1^2-x2^2]
=b[(x1-x2)(x1+x2)]
sachant que x appartient à [0 50] :
|f(x2)-f(x1)|<=b*50*|x1-x2|
Donc L=b*50
sachant que |.| définie la norme euclidienne !
Est-je péché quelque part ?
donc :
f(x2)-f(x1)=-bx2^2+bx1^2
=b[x1^2-x2^2]
=b[(x1-x2)(x1+x2)]
sachant que x appartient à [0 50] :
|f(x2)-f(x1)|<=b*50*|x1-x2|
Donc L=b*50
sachant que |.| définie la norme euclidienne !
Est-je péché quelque part ?
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Oui, c'est ça à un détail près.
Tu as mis un 50? il faut justifier. C'est quoi la valeur maxi de (x1+x2)?
Tu as mis un 50? il faut justifier. C'est quoi la valeur maxi de (x1+x2)?
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Oui, la valeur max est 50 m/s, donc j'ai résonné sur le fait que je travaille sur la plage [0 50] tel que x1=0, x2=50,
Vrai au faux ???
Vrai au faux ???
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Mais c'est 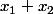 qu'on souhaite majorer et non pas et non pas |x1-x2|
qu'on souhaite majorer et non pas et non pas |x1-x2|
Re: Définir la constante Lipschitz de la fonction f(x)=-b(x^
Sinon on peut utiliser le théorème des accroissements finis pour montrer que la constante est égale au sup de la valeur absolue de f'(x) sur [0,50].
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
