Qu'en pensez vous ? voilà un phénomène assez étrange .... Chez moi, il fait toujours beau le 17 janvier !
En effet, entre 2012 et 2019, j'ai relevé quotidiennement la production électrique de l'installation photovoltaïque sur mon toit. Voici, classées de manière croissante, les productions (en kWh) quotidiennes entre les 7 et 27 janvier des 8 années :
- Code: Tout sélectionner
0,133
0,398
0,454
0,476
0,577
0,607
0,633
0,67
0,67
0,75
0,809
0,857
0,86
0,862
0,869
0,9
0,918
0,942
1,002
1,015
1,029
1,03
1,032
1,064
1,072
1,091
1,134
1,169
1,184
1,185
1,196
1,197
1,21
1,214
1,218
1,26
1,274
1,293
1,312
1,316
1,319
1,34
1,341
1,354
1,375
1,389
1,401
1,415
1,44
1,465
1,467
1,485
1,515
1,529
1,532
1,548
1,554
1,565
1,569
1,63
1,665
1,667
1,693
1,762
1,789
1,805
1,834
1,846
1,969
1,985
2,043
2,07
2,116
2,12
2,232
2,276
2,352
2,471
2,62
2,734
2,766
2,801
2,843
2,879
2,886
2,948
2,967
2,998
3,016
3,191
3,211
3,224
3,243
3,363
3,371
3,6
3,612
3,68
3,827
3,861
3,882
3,907
3,907
3,919
3,92
3,938
4,137
4,31
4,426
4,432
4,448
4,464
4,73
4,743
4,757
4,777
4,988
5,02
5,026
5,212
5,22
5,235
5,282
5,293
5,319
5,349
5,409
5,417
5,546
5,55
6,103
6,12
6,132
6,274
6,376
6,476
6,587
6,684
6,772
6,85
7,078
7,256
7,257
7,29
7,354
7,371
7,418
7,571
7,629
7,632
7,722
7,917
7,929
8,135
8,171
8,282
8,365
8,372
8,377
8,583
8,707
8,81
8,818
8,829
8,981
9,143
9,202
9,251
Cela représente 168 données : 8 nombres (car 8 ans) sur 21 jours (du 7 au 27 janvier).
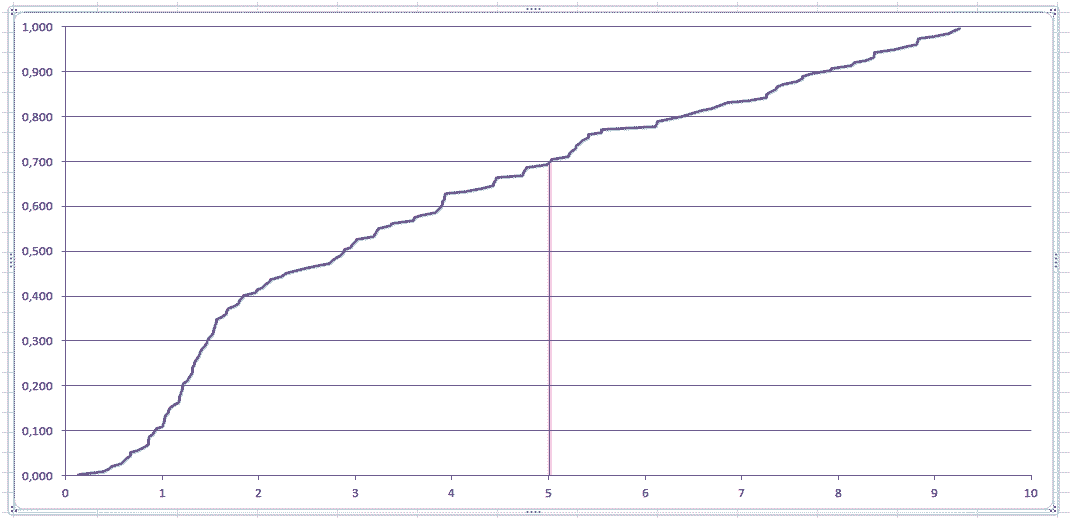
Voici la répartition des 168 nombres : en abscisse une production X (l'une des 168 listées au-dessus), en ordonnée le pourcentage Y des productions inférieures à X :
Voici en particulier les résultats du 17 janvier pendant les 8 années :
- Code: Tout sélectionner
5,026
8,171
8,981
6,376
6,12
9,202
7,418
8,372
On voit que le minimum est de 5,026
Si l'on replace ceci dans la répartition des 168 productions sur la période de janvier étudiée sur 8 ans, on voit que cette valeur 5.026 est à environ une hauteur des 30% des meilleures productions réelles : seulement 30% des productions quotidiennes sont supérieures (car 70% sont inférieures
Or, si on s'amuse à calculer la probabilité (avec les hypothèses qui conviennent) qu'un tel événement se réalise, à savoir que ce minimum sur 8 résultats, soit dans les 30% meilleures productions, on obtient la probabilité de 0.3^8 , à savoir 1 / 15000 environ. C'est extrêmement faible, même par rapport à 1 / 365 (qui représenterait un phénomène qui se réaliserait une fois par an en moyenne).
Ma question : comment expliquer un tel phénomène d'une probabilité aussi faible ?
Est-ce que le 17 janvier est un jour "divin" ?



