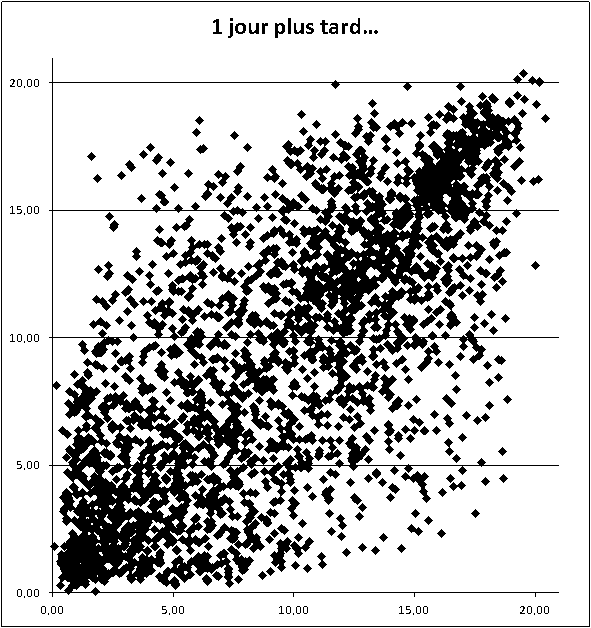
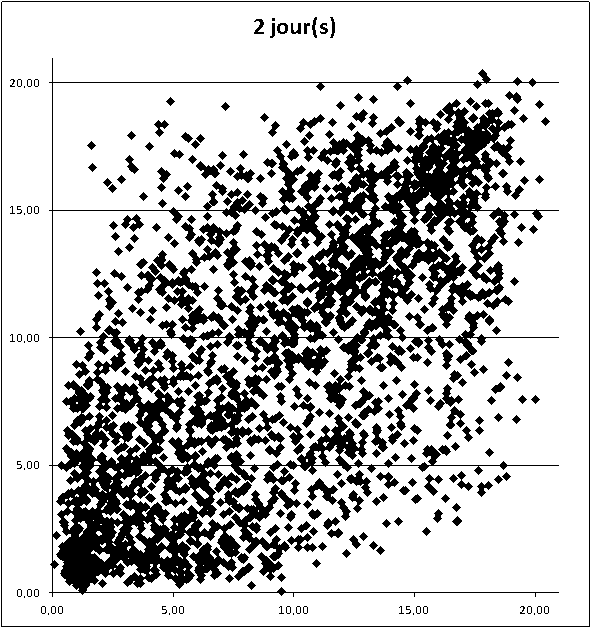
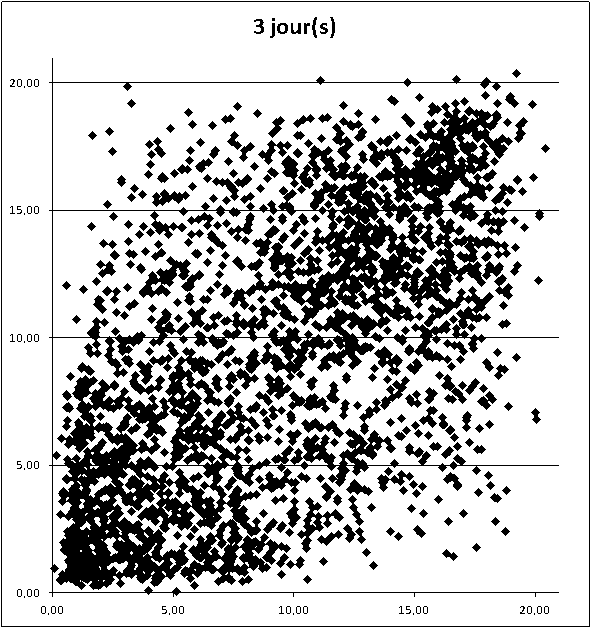
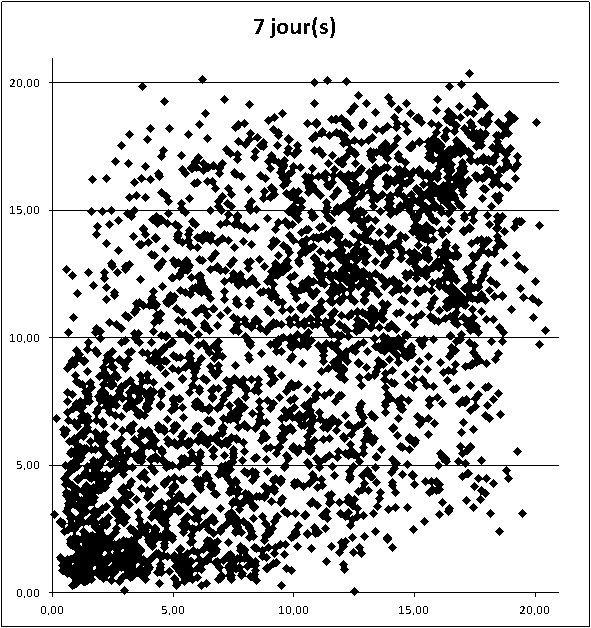
beagle a écrit:je redis ne pas aimer l'utilisation de jours complétement interchangeables vues les probas liées,
oui, c'est vrai que les journées sont liées, mais chaque production fait part entière de l'ensemble des productions possibles. Ce n'est pas parce que les variables X_i sont liées qu'elles ne suivent pas de loi de probabilité (qui , elle, est inconnue).
beagle a écrit:Mais sur une petite simulation plus réduit il m'a semblé que cela accentuait les extremes: on augmente à la fois les grosses réussites et les zeros partout sur deux ans par exemple.
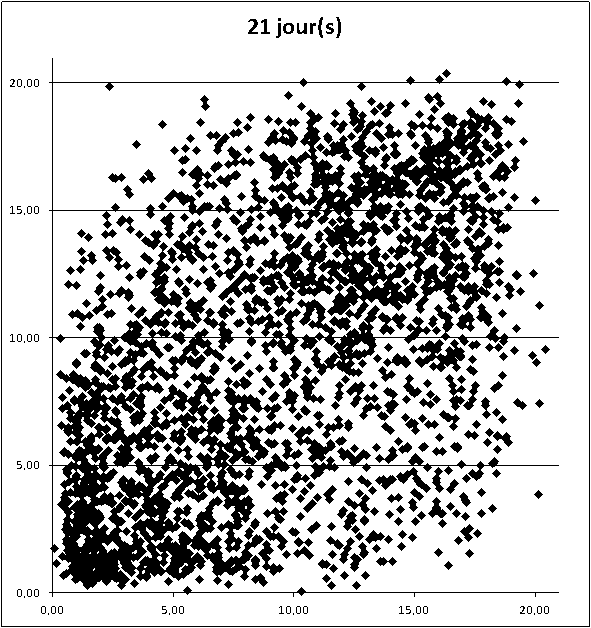
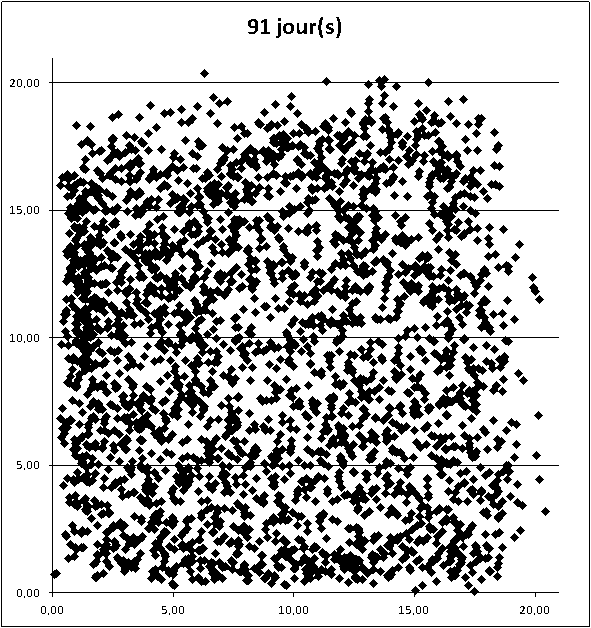
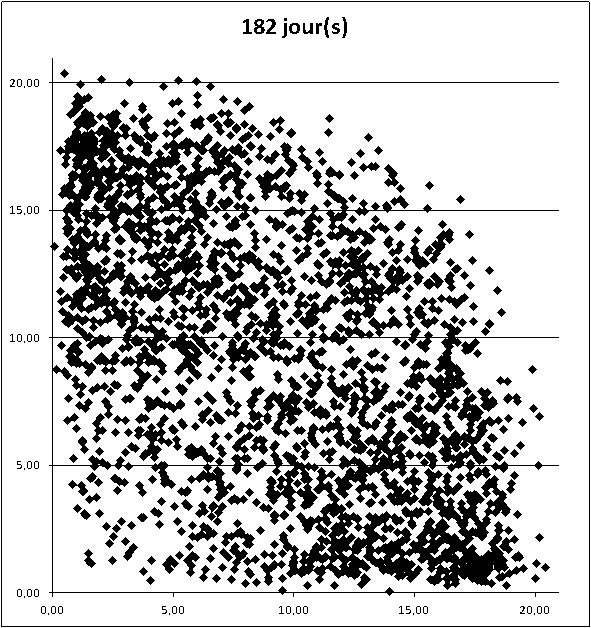
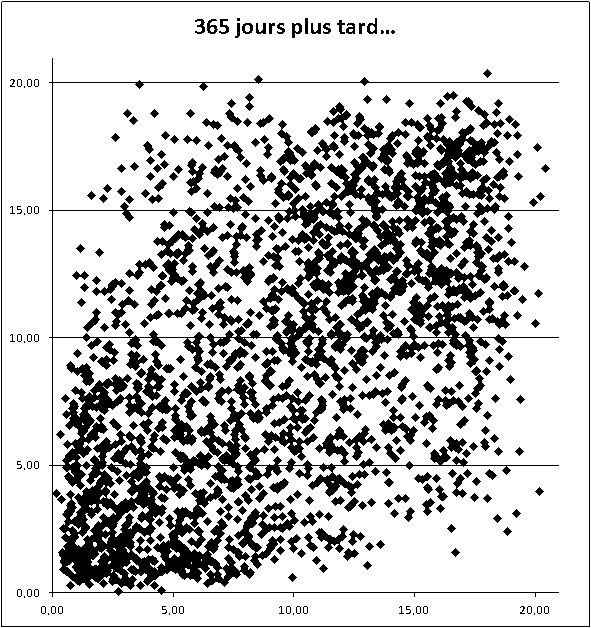
La distance que j'ai présentée ce matin ne donne pas l'avantage au minimum, ou au maximum, ou autre, car toutes les données sont prises en compte avec la même importance (c'est les variables U[i] centrées réduites)
Ce que mesure la "distance" D au-dessus, c'est un éloignement du tirage d'un jour fixé à un "tirage moyen"
(du coté du plus petit, ou du plus grand, ou au milieu...).
cela irait aussi? avec le fait que par exemple la ligne 3 deuxième jour est le pendant catastrophique du grand gagnant.
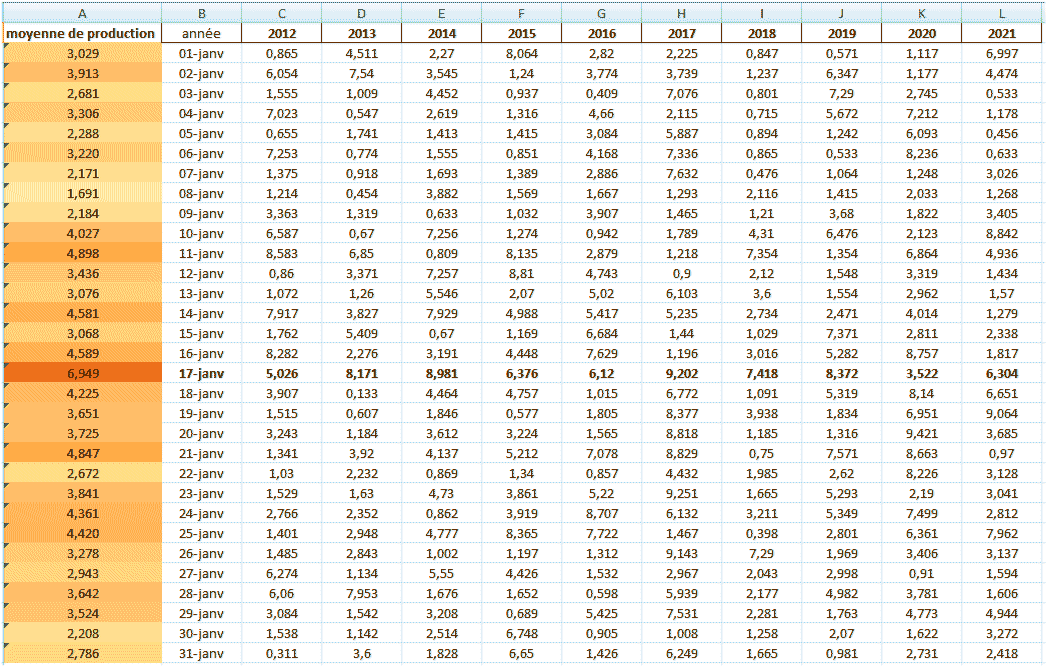
oui, mais pour étudier un jour, il faut connaitre ses jours voisins (j'ai fixé le voisinage à 10 jours). Or la tableau que j'ai donné ne présente pas toutes les données voisines du 8 janvier... donc tu ne peux pas conclure réellement. Il te faudrait un complément de données, que j'ai sur mon pc évidemment. Si je regarde le 8 janvier (avec les données des années 2011 à 2019), j'ai le tirage de boules T* = [20, 24, 63, 81, 96, 117, 146, 164] , et alors la distance au "tirage moyen" est D* = 1.74 . Comment interpréter ce 1.74 ? c'est plus grand que 1, donc le 3 janvier a l'air "assez loin du tirage moyen" , mais est-ce exceptionnel ? C'est là que je regarde l'ensemble des distances pour tous les jours de l'année, et je vois que 1.74 est la 21ème plus grande distance sur l'année, donc une journée comme ça est assez commune, je trouve. Le 14 janvier a un D* = 1.89 (qui est la 15ième plus grande distance sur l'année), donc un peu plus excentré...