Borne inf d'un ensemble
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2007, 12:53
par Joker62 » 24 Avr 2007, 12:53
Allez un exo sympathique pour Sandrine ou pour tous les autres d'ailleurs

Il m'a surpris et me surprend toujours, c'est pour ça que je vous le propose

Démontrer que

existe et le déterminer.
Si besoin d'une indication y'a pas de souci.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Avr 2007, 16:47
par Imod » 24 Avr 2007, 16:47
Bonjour Joker .
Une solution qui manque vraiment d'élégance :
On note
=(x^2-ax-b)^2=x^4-2ax^3+(a^2-2b)x^2+2abx+b^2)
Une primitive de

est donnée par :
F(x) =
x^3+abx^2+b^2x)
.
En notant I(a,b) l'intégrale proposée :
=\frac{1}{5}-\frac{1}{2}a+\frac{1}{3}(a^2-2b)+ab+b^2)
=b^2+(a-\frac{2}{3})b+(\frac{1}{3}a^2-\frac{1}{2}a+\frac{1}{5}))
Pour

fixé
)
est minimun quand

( parabole ) . Alors :
=\frac{1}{3}[\frac{a^2}{4}-\frac{a}{2}+\frac{4}{15}])
Donc
)
est minimum quand
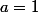
alors
=I(1,-\frac{1}{6})=\frac{1}{180})
.
Aux erreurs de calcul près .
Imod
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 24 Avr 2007, 16:52
par serge75 » 24 Avr 2007, 16:52
Existence par non vide et minoré par 0.
Indication de calcul autre que la méthode de Imod : considérer ceci comme un problème de projection sur C([0,1],R) muni du produit scalaire usuel, en projetant l'application x->x² sur l'ensemble des fonctions affines.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2007, 16:54
par Joker62 » 24 Avr 2007, 16:54
Ouahhhh :)
Excellent aussi en fait ;)
Et donc oui c'est bien 1/180 la réponse :)
En fait, ce qui m'a frappé dans cet exo, c'est qu'à première vue, on dirait un problème d'analyse, et que la façon dont on l'a résolu était basé sur de l'algèbre pur et dur ! :)
En fait, on munissait l'ensemble des fonctions continues par le produit scalaire intégrale de 0 à 1 f(t)g(t) dt
Et donc il suffit de prendre F le sous espace des fonctions polynomiales à coeff réels, de degrés inférieur ou égale à 1
On fait le projeté orthogonale de f(x) : x -> x², sur F et voilà on arrive au même résultat.
Mais j'avoue, la version analyse est pas mal aussi :)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2007, 16:55
par Joker62 » 24 Avr 2007, 16:55
Bon ben vous conaissez tout ! S'pas marrant lol
 par sandrine_guillerme » 24 Avr 2007, 17:53
par sandrine_guillerme » 24 Avr 2007, 17:53
Joker62 a écrit:Allez un exo sympathique pour Sandrine
C'est gentil ça

La prochaine fois, j'aurais aimé un exo d'algèbre... !
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2007, 18:02
par Joker62 » 24 Avr 2007, 18:02
Beuh c'est un exo d'algèbre aussi
C'est pour ça que je l'ai posté, car à première vue, on croit qu'il s'agit d'un problème d'analyse :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
 existe et le déterminer.
existe et le déterminer. existe et le déterminer.
existe et le déterminer.