Deux camions et un pendule :)

Bonsoir,

Voici un autre exercice, que cette fois-ci je n'ai pas réussi à résoudre tout seul :

Nous avons deux camions, sur le premier camion une colonne est posée avec au bout un fil, à ce fil est attaché une boule de masse . La masse du fil et la colonne sont négligeables. Ce camion avance à une vitesse V. A un instant donné, ce camion "rentre" dans un deuxième camion et reste collé avec. Le deuxième camion a une masse m.

Si l'on sait que R est la longueur du fil, calculer la vitesse initiale minimale V (du premier camion), tel que la boule effectue un mouvement circulaire autour du point P. On suppose que M, m >> , qu'il n'y a pas de frottements, et que la tension dans le fil est T.

========================================================================

Ce que j'ai commencé à faire, c'est calculer la vitesse commune du camion 1 et 2 après l'impact, je trouve U = , ensuite j'ai du mal à faire le lien avec la masse et le fil.

Question : quand le camion avance au début avec une vitesse V, la masse est dans quel état ? Je veux dire, si on regarde le dessin ci-joint, le fil est "soulevé" d'un angle disons ce qui me paraît étrange aucune force ne s'applique sur la masse vers la droite il me semble ?

Merci d'avance pour votre aide. (Si vous pouviez me montrer la voie).

Salut,

Exact, si le camion arrive à vitesse v constante, nous pouvons supposer que l'angle alpha est égal à 0 (par rapport à un axe vertical descendant Oz) tout en négligeant les frottements de l'air. C'est comme si t'es dans une voiture. Quand elle accélère, t'es collé contre ton siège, quand elle avance à vitesse constante, ya "rien" qui se passe et lorsqu'elle décélère, tu es projeté vers l'avant.
Par contre, si le camion heurte le deuxième véhicule, il y aura une décélération brutale, qui engendrera un mouvement de la boule au niveau du pendule.
Je pense que l'on écrit alors le PFD et en utilisant quelques théorèmes énergétiques, on devrait s'en sortir... à voir !

Kikoo <3 Bieber a écrit:Salut,

Exact, si le camion arrive à vitesse v constante, nous pouvons supposer que l'angle alpha est égal à 0 (par rapport à un axe vertical descendant Oz) tout en négligeant les frottements de l'air.
Par contre, si le camion heurte le deuxième véhicule, il y aura une décélération brutale, qui engendrera un mouvement de la boule au niveau du pendule.
Je pense que l'on écrit alors le PFD et en utilisant quelques théorèmes énergétiques, on devrait s'en sortir... à voir !

Bonsoir,

Merci pour ta réponse. On est d'accord pour le début. Au moment du choc, le pendule part avec une vitesse V-U. U étant la vitesse commune aux deux camions après le choc.

U =

Bon ensuite, effectivement en utilisant l'énergie ça peut marcher, seulement je ne sais que faire de la tension T donné dans l'énoncé..

Un avis ?

Merci bien

Je pense qu'il faut que tu trouves l'expression de la tension avec le PFD. Le problème, c'est que tu te retrouveras avec du theta (angle formé par le pendule) et du "theta point", donc tu devras passer par le TEC pour régler le problème, ou un truc de ce type. Je m'y pencherai demain ;)
Bonne nuit !

Kikoo <3 Bieber a écrit:Je pense qu'il faut que tu trouves l'expression de la tension avec le PFD. Le problème, c'est que tu te retrouveras avec du theta (angle formé par le pendule) et du "theta point", donc tu devras passer par le TEC pour régler le problème, ou un truc de ce type. Je m'y pencherai demain
Bonne nuit !

Thx ,

Je vais aussi tenter de suivre ce chemin là.

Bonne nuit !

Re,

En ne tenant pas compte de l'info sur la tension, j'aboutis à ceci :

Salut,

La tension peut normalement te servir.
En effet, on sait que pour une mouvement circulaire uniforme, l'accélération centripète vaut v²/R (ce v ici n'a rien à voir avec le v de ton exercice).
Or, d'après le PFD, cette accélération fois la masse m vaut T + la projection du poids.

Quand on est au sommet de la trajectoire, on a donc v²/R = g + T/m donc T = m*v²/R - mg.

Or, T étant une tension dans un fil, T ne peut pas être négatif. La condition est donc T >=0 ce qui se réécrit v²/R >= g donc v >= racine(g*R).

Benjamin a écrit:Salut,

La tension peut normalement te servir.
En effet, on sait que pour une mouvement circulaire uniforme, l'accélération centripète vaut v²/R (ce v ici n'a rien à voir avec le v de ton exercice).
Or, d'après le PFD, cette accélération fois la masse m vaut T + la projection du poids.

Quand on est au sommet de la trajectoire, on a donc v²/R = g + T/m donc T = m*v²/R - mg.

Or, T était une tension dans un fil, T ne peut pas être négatif. La condition est donc T >=0 ce qui se réécrit v²/R >= g donc v >= racine(g*R).

Oui oui tout à fait, elle me sert en faite à justifier comment j'arrive à l'expression de la vitesse critique racine(g*R).

Admettons que le pendule est à la verticale (pour des raisons d'équilibre il ne peut être positionnée différemment). Après le choc, admettons qu'il soit animé d'une vitesse v_1.

1. Quelle est sa vitesse lorsqu'il est monté (rotation de 180 degrés) ?
2. Quelles sont les deux forces qui agissent sur la masse ?
3. Laquelle est toujours présente ?
4. Laquelle sert à ce que la masse reste accrochée au fil ?
5. Quelle est la condition sur l'accélération (ou la force) pour que la masse suive un mouvement circulaire ?

Une fois que tu as répondu à ces questions, peut-être que tu pourras traduire la condition minimale pour avoir un mouvement circulaire (condition sur la vitesse de la masse, qui ensuite doit être traduite en termes de vitesse du camion)

EDIT: devancé

Vie89 a écrit:Re,

En ne tenant pas compte de l'info sur la tension, j'aboutis à ceci :

La réponse finale me semble correcte ... mais pour y arriver, on doit tenir compte que le fil reste tendu, donc de la tension du fil.

Ma façon de faire (qui aboutit à la même réponse finale que la tienne) :

MV = (M+m).V1 (avec V la vitesse du camion M avant impact et v1 la vitesse des camions après impact (référentiel terrestre))

V1 = M/(M+m) . V

V - V1 = V - M/(M+m) . V

V - V1 = V.(M+m-M)/(M+m)

V - V1 = V.m/(M+m)

Donc si on prend, après le choc, un référentiel lié aux camions (qui alors est galiléen puisque V1 = cte dans un référentiel terrestre), la masse µ est animée en t = 0 (moment du choc) d'une vitesse Vo = V.m/(M+m)

Lorsque le fil est vertical avec la masse µ en haut (pourvu qu'elle y arrive), on a :

Energie cinétique au point bas + travail du poids de la masse µ = Energie cinétique au point haut.

(1/2).µ.Vo² - 2µgR = (1/2).µ.Vh² avec vh la vitesse de la masse µ au point haut (référentiel lié aux camions).

vh² = Vo² - 4gR

Et pour que le tour se poursuive, fil tendu, il faut que : µ.vh²/R >= µ.g

(Vo² - 4gR)/R >= g

Vo² >= 5gR

Vo >= racinecarrée[5gR]

Vo min = racinecarrée[5gR]
*****
V - V1 = Vo
V = V1 + racinecarrée[5gR]
V = M/(M+m) . V + racinecarrée[5gR]
V(1 - M/(M+m)) = racinecarrée[5gR]
V(m/(M+m)) = racinecarrée[5gR]

V = [(M+m)/m].racinecarrée[5gR]
vitesse du camion avant collision (référentiel terrestre).

:zen:

J'aboutis également à la même réponse. Cependant, ma question à Vie89 est la suivante : pourquoi se met-on dans un référentiel lié au camion après le choc ?

Mathusalem a écrit:J'aboutis également à la même réponse. Cependant, ma question à Vie89 est la suivante : pourquoi se met-on dans un référentiel lié au camion après le choc ?

Bonsoir tout le monde,

Bon j'ai vu que mon résultat était apparemment bon donc c'est déjà ça, je crois avoir saisis pour la tension, pour ce qui est de ta question Mathusalem, tu as raison de la poser !
Intuitivement j'ai posé le V-U pour le pendule, mais en voyant le détail de Black Jack par exemple, je ne suis plus sûr d'avoir compris à 100%.

Disons que après le choc, les deux camions partent à la vitesse commune U, et que cette vitesse commune est dans le sens opposée à celle de V ?

Merci de m'éclairer si je me trompe. Car au final le plus important n'est pas d'avoir le bon résultat..

Lorsque les deux camions entrent en collision, tu peux calculer leur vitesse commune en négligeant la masse du pendule. Tu trouves une vitesse

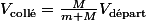
La force de contact n'a agit que sur le camion, et non sur le pendule, ainsi la vitesse du pendule reste non modifée. Donc sa vitesse est .

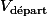
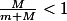
On peut se convaincre par le fait que que la vitesse du pendule est supérieure à la vitesse des camions collés. Ainsi, le poteau tenant le pendule a une vitesse moindre que le pendule. Donc, par rapport au poteau, le pendule est animé d'une vitesse vers la droite, et donc pourra tourner autour du poteau.

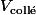
Maintenant, on pourrait faire toute l'analyse dans le référentiel terrestre où le camion a une vitesse et le pendule une vitesse .

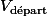
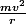
Le problème est le suivant : quand tu dis qu'une force centripète doit être de magnitude pour contraindre un objet de vitesse v à se mouvoir sur un cercle de rayon r, la vitesse v est prise relative à la vitesse du centre de rotation. C'est-à-dire que c'est valable pour un centre de rotation de vitesse 'nulle'.

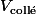
Ici, ce n'est pas le cas, le centre de rotation (le poteau) se déplace à , donc tu ne peux pas prendre la vitesse du pendule dans le référentiel terrestre pour trouver la norme de la force centripète et en déduire ta condition critique, car dans le référentiel terrestre, le pendule fait un mouvement cycloïdal (un cercle qui se déplace). Tu trouverais une force centripète trop grande.

D'où l'utilité de te mettre dans un référentiel qui se déplace à

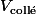
Ainsi, la vitesse du camion est nulle, et la vitesse du pendule devient .

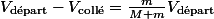
Dans ce référentiel, le pendule fait bien une rotation autour d'un centre de rotation fixe, puisque le poteu avait la vitesse du camion, (v_collé) qui dans ce référentiel est nulle.

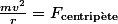
Donc, dans ce référentiel,tu peux tranquillement appliquer la relation et finir ton calcul.

J'espère que cela clarifie les choses.

Black Jack se met dans un référentiel lié au camion après le choc, en déduit la condition critique, puis revient dans le référentiel terrestre ensuite. Ce n'est pas entièrement nécessaire.

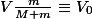
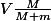
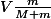
Il pourrait se passer de renommer et raisonner sur la première expression pour obtenir une condition sur V, qui ci-dessus est la vitesse de départ, donc la vitesse du camion. V est la vitesse de départ. est la vitesse du camion dans le référentiel terrestre après collision. est la vitesse du pendule dans le référentiel lié au camion.

J'espère que cela clarifie les choses.

Sinon, essaie de faire tes calculs dans le référentiel terrestre. Applique la conservation de l'énergie mécanique pour trouver la vitesse du pendule en haut du cercle, et applique la condition critique. Tu verras que tu trouveras au final une réponse

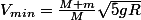
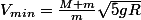
au lieu de qui est faux, car tu auras appliqué ta condition critique par la force centripète à une vitesse à laquelle tu ne peux pas l'appliquer.

Mathusalem a écrit:D'où l'utilité de te mettre dans un référentiel qui se déplace à

Ainsi, la vitesse du camion est nulle, et la vitesse du pendule devient .

Re, très bonne explication, je te remercie. Je souligne tout de même ce passage.

Quand je me place dans le référentiel du pendule, pourquoi n'ai-je pas , car intuitivement le V de départ est dans le même sens que le V collision non ? J'avais d'ailleurs fait ça au départ, et ça ne tombait pas juste bien sûr.

Merci bien

Petite astuce : Pour mettre des accents aigüs en LaTeX, tu peux faire \acute{*lettre*}

Vie89 a écrit:Re, très bonne explication, je te remercie. Je souligne tout de même ce passage.

Quand je me place dans le référentiel du pendule, pourquoi n'ai-je pas , car intuitivement le V de départ est dans le même sens que le V collision non ? J'avais d'ailleurs fait ça au départ, et ça ne tombait pas juste bien sûr.

Merci bien

Tu ne te mets pas dans le référentiel du pendule (ça serait embêtant car il n'est pas d'inertie - pourquoi?) mais dans le référentiel du camion.

Avant la collision, et le pendule et le camion vont à

Après la collision, la force n'ayant agit que sur le camion on a


Vitesse du pendule
Vitesse du camion

Maintenant, si toi tu observes le camion et le pendule depuis le sol (référentiel terrestre) tu vois un camion qui a une certaine vitesse, et un pendule qui initialement à une vitesse supérieure. Toutes les deux vitesses sont dirigées vers l'avant.

Cependant, si tu l'observes depuis une voiture qui se déplace à la vitesse du camion, le camion est immobile, et le pendule a une vitesse initiale toujours vers l'avant, mais plus petite qu'avant.

Pour fixer les idées, si tu as un mobile qui va à 5m/s et un autre qui va à 12m/s, et que tu les observes ensuite depuis une voiture qui va à 8m/s, alors tu auras l'impression que le premier mobile se déplace à (5-8) = -3 m/s (recule) et que l'autre se déplace à 12-8 = 4 m/s.

Donc, la loi c'est bien

Nouvelle vitesse = Vitesse dans le référentiel 1 - Vitesse du nouveau référentiel par rapport au référentiel 1.

Ici, clairement, la nouvelle vitesse du pendule sera



Est-ce que ça te semble logique ?

@Kikoo, en Latex, normalement \' devrait faire l'affaire Merci du conseil

Mathusalem a écrit:Tu ne te mets pas dans le référentiel du pendule (ça serait embêtant car il n'est pas d'inertie - pourquoi?) mais dans le référentiel du camion.

Avant la collision, et le pendule et le camion vont à

Après la collision, la force n'ayant agit que sur le camion on a


Vitesse du pendule
Vitesse du camion

Maintenant, si toi tu observes le camion et le pendule depuis le sol (référentiel terrestre) tu vois un camion qui a une certaine vitesse, et un pendule qui initialement à une vitesse supérieure. Toutes les deux vitesses sont dirigées vers l'avant.

Cependant, si tu l'observes depuis une voiture qui se déplace à la vitesse du camion, le camion est immobile, et le pendule a une vitesse initiale toujours vers l'avant, mais plus petite qu'avant.

Pour fixer les idées, si tu as un mobile qui va à 5m/s et un autre qui va à 12m/s, et que tu les observes ensuite depuis une voiture qui va à 8m/s, alors tu auras l'impression que le premier mobile se déplace à (5-8) = -3 m/s (recule) et que l'autre se déplace à 12-8 = 4 m/s.

Donc, la loi c'est bien

Nouvelle vitesse = Vitesse dans le référentiel 1 - Vitesse du nouveau référentiel par rapport au référentiel 1.

Ici, clairement, la nouvelle vitesse du pendule sera



Est-ce que ça te semble logique ?

@Kikoo, en Latex, normalement \' devrait faire l'affaire Merci du conseil

TOUT A FAIT. C'est très clair, merci beaucoup. Je me suis emmêlé les pinceaux en écrivant, je ne voulais pas dire référentiel du pendule.
J'ai déjà fais d'autres exos de ce type, mais là j'avais du mal à faire le lien entre les 2 "parties" du problème. Bref, c'est maintenant bien clair.
Je n'hésiterai à partager avec vous d'autres problèmes si besoin est.

Encore merci Mathusalem, et merci à tous les autres également !

A bientôt :lol3:

Le point le plus important c'est que tu fais ce changement de repère pour analyser un mouvement circulaire (le centre du cercle - le camion, est immobile) et non un mouvement cycloïdal (le centre du cercle se déplace - à la vitesse du camion).

Mathusalem a écrit:Le point le plus important c'est que tu fais ce changement de repère pour analyser un mouvement circulaire (le centre du cercle - le camion, est immobile) et non un mouvement cycloïdal (le centre du cercle se déplace - à la vitesse du camion).

C'est noté, je vais pouvoir refaire ça au propre clairement.

Merci bien