Second degré - substitution pour résoudre un quatrième degré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 29 Sep 2012, 23:56
par upium666 » 29 Sep 2012, 23:56
Bonjour à tous et à toutes !
On a :
=x^4-mx^2+m-1)
où

est l'inconnue et

un paramètre réel.
La question est la suivante :
Pour quelles valeurs de

l'équation
=0)
admet-elle quatre solutions distinctes ?
(En utilisant des notions relatives aux fonctions du second degré seulement)
J'ai pensé à pose
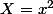
Cela nous donnera :
=0\Leftrightarrow X^2-mX+m-1=0 \\ \Delta = m^2-4m+4 = (m-2)^2)
Et après ?
-
low geek
- Membre Relatif
- Messages: 318
- Enregistré le: 02 Jan 2011, 19:09
-
 par low geek » 30 Sep 2012, 00:05
par low geek » 30 Sep 2012, 00:05
Hey!
pour que f(x) admette 4 solutions distinctes il faut que delta >0 (pour que ton
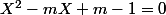)
avec X1 et X2 distincts.
donc tu dois résoudre (m-2)² >0 ce qui n'est pas compliqué : R/ {2}

-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 30 Sep 2012, 00:13
par upium666 » 30 Sep 2012, 00:13
low geek a écrit:Hey!
pour que f(x) admette 4 solutions distinctes il faut que delta >0 (pour que ton
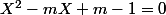)
avec X1 et X2 distincts.
donc tu dois résoudre (m-2)² >0 ce qui n'est pas compliqué : R/ {2}

Je pense que tu es tombé dans le piège :
Il faut une deuxième condition qui est :
X1 et X2 positifs ! :lol3:
Cordialement.
-
low geek
- Membre Relatif
- Messages: 318
- Enregistré le: 02 Jan 2011, 19:09
-
 par low geek » 30 Sep 2012, 00:31
par low geek » 30 Sep 2012, 00:31
Exact. Du coup il faut écrire les deux solutions et résoudre les deux inéquations pour trouver le bon intervale.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Sep 2012, 06:40
par chan79 » 30 Sep 2012, 06:40
upium666 a écrit:Bonjour à tous et à toutes !
On a :
=x^4-mx^2+m-1)
où

est l'inconnue et

un paramètre réel.
La question est la suivante :
Pour quelles valeurs de

l'équation
=0)
admet-elle quatre solutions distinctes ?
(En utilisant des notions relatives aux fonctions du second degré seulement)
J'ai pensé à pose
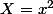
Cela nous donnera :
=0\Leftrightarrow X^2-mX+m-1=0 \\ \Delta = m^2-4m+4 = (m-2)^2)
Et après ?
Bonjour
Pas besoin de poser X=x² ici puisque 1 et -1 sont de toutes façons des solutions quel que soit m
x;)-mx²+(m-1)=x;)-1 -m(x²-1)=(x²-1)(x²+1-m)=(x-1)(x+1)(x²+1-m)
si m=1 on a 3 solutions {-1,1,0)
si m1 les solutions sont {1, -1,
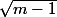
et
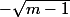
}ce qui en fait 4 sauf dans le cas m=2 où il y a seulement deux solutions {-1;1}
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
avec X1 et X2 distincts.
où
est l'inconnue et
un paramètre réel.
l'équation
admet-elle quatre solutions distinctes ?