Petit problème : équation du quatrième degré ...

par **Flori@n** » 22 Oct 2006, 20:27

Bonsoir à tous ... j'ai un exercice qui porte sur les equation symétrique du quatrième degré.

j'ai une question qui me pose problème ... bien ue ça doit être un truc tout bête ... :marteau:

(E) désigne l'équation x^4 - 4x^3 + 2x^2 - 4x + 1 = 0

Démontrer que si x (indice 0) avec est solution de (E) alors 1/x (indice 0) est solution de (E)

la je suis bloqué ... quelqu'un pourrait il m'éclairer :id:

merci d'avance

par **flaja** » 22 Oct 2006, 20:30

bonsoir,
diviser par x^2
et changer de variable X = x + 1/x

par **matteo182** » 22 Oct 2006, 20:34

Salut,
Calcule l'expression

pour

. Ensuite tu réduis tout au même dénominateur et observe alors le numérateur que tu vas obtenir. Ca s'arrange bien comme on veut.

par **Flori@n** » 22 Oct 2006, 20:40

merci ... mais ça je l'ai fait dans les questions suivantes ...

voici les questions suivantes :

a) question posant problème ( voir premier message)

b) Montrer que l'équation (E) est équivalente à l'équation :

x^2 - 4x + 2 - (4/x) + 1/(x)^2 = 0

C'est dans cette question que j'ai divisé par x^2

c) calculer (x + 1/x)^2

ça ça donne x^2 + 2 + 1/(x)^2

e) en posant X = x + 1/x, montrer que l'équation :

x^2 - 4x + 2 - (4/x) + 1/(x)^2 = 0 se ramène a une equation du second degré.

la ça me donne X^2 - 4x - (4/x) ... mais est-ce correct ?

du coup ... si on divise par x¨2 et on se donne X = x + 1/x dans les questions suivantes ..; comment faudrait il faire pour démontrer la question a) ? :marteau:

par **Flori@n** » 22 Oct 2006, 20:41

désolé matteo j'écrivais mon dernier message et je n'ai pas vu le tien avant ... je vais faire comme tu dis et je vous dis si je trouve :happy2: merci

par **Flori@n** » 22 Oct 2006, 20:48

Merci matteo, j'ai trouvé, merci ! (enfin ... tu as trouvé ... :id: re merci

)

Merci aussi flaja :id:

juste encore une toute petite question ...

pour le e) de mon exercice :
en posant X = x + 1/x, montrer que l'équation :

x^2 - 4x + 2 - (4/x) + 1/(x)^2 = 0 se ramène a une equation du second degré.

la ça me donne X^2 - 4x - (4/x) ... mais est-ce correct ? ou il y a encore autre chose ...

car après je dois résoudre l'équation du second degré, puis en déduire les solutions de l'équation (E) mais ... je suis bloqué ... (a nouveau) :S

par **matteo182** » 22 Oct 2006, 20:55

Soit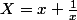

En calculant X² on trouve :

Ce que tu avais bien remarqué et donc ton équation devient :

Ce que tu as trouvé.
Mais il ne faut pas s'arrêter la, puisque on a encore du "x" dans l'équation, et on veut simplement du "X".
Il faut donc changer l'écriture :

Tu peux ici terminer en remplacant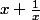

par ton X et voila c'est gagné.

par **Flori@n** » 22 Oct 2006, 21:02

Encore merci !!!! :id: :id: :id:

je vais donc revoir ça et remettre ça au propre !

Bonne soirée à vous !

Petit problème : équation du quatrième degré ...

petit problème : équation du quatrième degré ...

Qui est en ligne