Résolution équation
21 messages
- Page 1 sur 2 - 1, 2
Résolution équation
Bonjour,
Je vais rentrer en 1ère S et les devoirs de vacances s'imposent donc ! :3
Je travaille sur les suites en ce moment et j'ai du mal pour une question. Il s'agit de déduire l'expression d'une suite u en fonction d'un entier naturel n à partir d'une suite v déjà exprimée en fonction de n. Je tombe donc sur l'équation suivante : (uñ-1)/(uñ+2)=((-1/2)^n)*2/5.
Je tourne en rond... Pouvez-vous m'aider svp ?
Ps : ñ signifie indice n
Merciz
Je vais rentrer en 1ère S et les devoirs de vacances s'imposent donc ! :3
Je travaille sur les suites en ce moment et j'ai du mal pour une question. Il s'agit de déduire l'expression d'une suite u en fonction d'un entier naturel n à partir d'une suite v déjà exprimée en fonction de n. Je tombe donc sur l'équation suivante : (uñ-1)/(uñ+2)=((-1/2)^n)*2/5.
Je tourne en rond... Pouvez-vous m'aider svp ?
Ps : ñ signifie indice n
Merciz
Re: Résolution équation
Hello,
S'agit-il bien de:
^n)
et tu veux isoler Un?
S'agit-il bien de:
et tu veux isoler Un?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résolution équation
Que donne un produit en croix?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résolution équation
C'est quoi la suite  ? Elle pourrait aussi servir d'étape pour le calcul de la suite
? Elle pourrait aussi servir d'étape pour le calcul de la suite  .
.
Re: Résolution équation
Bonjour, je vais faire le produit en croix ce soir, j'essayais bêtement de tomber sur un produit nul. Quant à v, c'est Vn=(Un-1)/(Un+2).
Merci et je vous recontacte ce soir
Merci et je vous recontacte ce soir
Re: Résolution équation
bjr,
Vn=(Un -1)/(Un+2)=(Un+2 -3)/(Un+2)=1-3/(Un+2)
donc
1-Vn=3/(Un+2)
et l'inverse donne
1/(1-Vn)=(Un+2)/3 = Un/3 +2/3
soit 3[1/(1-Vn) -2/3] =Un
donc Un= 3/(1-Vn) -2 puis tu remplaces Vn par sa valeur
Vn=(Un -1)/(Un+2)=(Un+2 -3)/(Un+2)=1-3/(Un+2)
donc
1-Vn=3/(Un+2)
et l'inverse donne
1/(1-Vn)=(Un+2)/3 = Un/3 +2/3
soit 3[1/(1-Vn) -2/3] =Un
donc Un= 3/(1-Vn) -2 puis tu remplaces Vn par sa valeur
Re: Résolution équation
Bonjour, le produit en croix ne m'a pas avancé. Avec la dernière solution du forum je tombe sur Un=(5*2n+4)/(5*2n-2) si n est pair et Un=(5*2n-4)/(5*2n+2) si n est impair. Cela me paraît incohérent, n'y aurait-il pas moyen de simplifier cela ?
Merci pour votre temps
Merci pour votre temps
Re: Résolution équation
C'est malheureusement devenu... assez incompréhensible.
Peux-tu donner l'énoncé complet (et dans l'ordre...) ? Si tu le souhaites, tu peux essayer d'écrire les formules mathématiques en prenant connaissance du guide (dans la section ' guide d'utilisation')
Que veux-tu faire avec Un ? Que vient faire Vn là-dedans ?
Soit: Tu as une suite Un dont tu veux une expression explicite en passant par une suite auxiliaire Vn
Soit: Tu as déjà utilisé Vn et tu veux qu'on t'aide à simplifier la formule explicite
Soit: Autre chose ....
Peux-tu donner l'énoncé complet (et dans l'ordre...) ? Si tu le souhaites, tu peux essayer d'écrire les formules mathématiques en prenant connaissance du guide (dans la section ' guide d'utilisation')
Que veux-tu faire avec Un ? Que vient faire Vn là-dedans ?
Soit: Tu as une suite Un dont tu veux une expression explicite en passant par une suite auxiliaire Vn
Soit: Tu as déjà utilisé Vn et tu veux qu'on t'aide à simplifier la formule explicite
Soit: Autre chose ....
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résolution équation
On peut écrire la suite sous la forme (en inversant numérateur et dénominateur): ^nu_{n-1}) , En calculant la différence d'indices
, En calculant la différence d'indices -(n-1)=3) ceci nous montre que nous passons au 3ème éléments chaque fois, ceci veut dire que pour:
ceci nous montre que nous passons au 3ème éléments chaque fois, ceci veut dire que pour:
 sera calculé en fonction de
sera calculé en fonction de 
 sera calculé en fonction de
sera calculé en fonction de 
 sera calculé en fonction de
sera calculé en fonction de 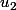
On peut considérer que ce sont 3 suites indépendantes mais qui ont la même structure. Calculons à partir du cas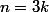 , les deux autres pourront être calculés par un changement d'indice.
, les deux autres pourront être calculés par un changement d'indice.
^{n-2}u_{n-3})
^{n-5}u_{n-6})

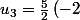^{1}u_{0})
Donc, pour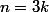 :
:
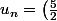^{n/3}\left (-2 \right )^{1+\hdots+(n-5)+(n-2)}u_0)
pour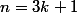 :
:
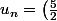^{(n-1)/3}\left (-2 \right )^{1+\hdots+(n-5)+(n-2)}u_1)
pour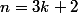 :
:
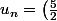^{(n-2)/3}\left (-2 \right )^{1+\hdots+(n-5)+(n-2)}u_2)
+(n-2)= ???) facile à calculer
facile à calculer
On peut considérer que ce sont 3 suites indépendantes mais qui ont la même structure. Calculons à partir du cas
Donc, pour
pour
pour
Re: Résolution équation
Bonjour, merci Razes mais c'est Vn qui vaut 2/5*(-1/2)^n
Voici l'énoncé complet et mes réponses :
On considère la suite Un avec n>=0 définie par :
U0(0=zéro..)= 3
Un+1(en indice)=2/(1+Un)
1) calculer U1 et U2. Cette suite est elle arithmétique ou géométrique ?
->U1=1/2 et U2=4/3. De plus on remarque que le quotient de deux termes consécutifs n'est pas constant, elle n'est donc pas géométrique.
2) déterminér une fonction f telle que pour tout n appartenant aux entiers naturels, Un+1(n+1 en indice)=f(Un)
Puis résoudre f(x)=x
->f(x)=2/(1+x) et les solutions de l'équation sont x=1 et x=-2
3) on considère la suite Vn avec n>=0 définie sur N par :
Vn=(Un-1)/(Un+2) ( rien n'est en indice)
a) calculer V0,V1 et V2
->respectivement on trouve 2/5, -1/5 et 1/10
b) démontrer que la suite est géo
->Vn+1(en indice)=(1-Un)/(4+2Un)
Or [(1-Un)/(4+2Un)]*(-2)=Vn
D'où (1-Un)/(4+2Un)=(-1/2)*Vn
C'est donc une suite géo de raison -1/2 et de premie terme 2/5
c)exprimer pour tout entier naturel n, Vn en fonction de n
-> Vn=V0*q^n
Vn=(2/5)*(-1/2)^n où q est la raison
d) en déduire pour tout entier naturel n, Un en fonction de n
Merci de votre aide
Voici l'énoncé complet et mes réponses :
On considère la suite Un avec n>=0 définie par :
U0(0=zéro..)= 3
Un+1(en indice)=2/(1+Un)
1) calculer U1 et U2. Cette suite est elle arithmétique ou géométrique ?
->U1=1/2 et U2=4/3. De plus on remarque que le quotient de deux termes consécutifs n'est pas constant, elle n'est donc pas géométrique.
2) déterminér une fonction f telle que pour tout n appartenant aux entiers naturels, Un+1(n+1 en indice)=f(Un)
Puis résoudre f(x)=x
->f(x)=2/(1+x) et les solutions de l'équation sont x=1 et x=-2
3) on considère la suite Vn avec n>=0 définie sur N par :
Vn=(Un-1)/(Un+2) ( rien n'est en indice)
a) calculer V0,V1 et V2
->respectivement on trouve 2/5, -1/5 et 1/10
b) démontrer que la suite est géo
->Vn+1(en indice)=(1-Un)/(4+2Un)
Or [(1-Un)/(4+2Un)]*(-2)=Vn
D'où (1-Un)/(4+2Un)=(-1/2)*Vn
C'est donc une suite géo de raison -1/2 et de premie terme 2/5
c)exprimer pour tout entier naturel n, Vn en fonction de n
-> Vn=V0*q^n
Vn=(2/5)*(-1/2)^n où q est la raison
d) en déduire pour tout entier naturel n, Un en fonction de n
Merci de votre aide
Re: Résolution équation
Pour la question 1 j'ai oublié de dire qu'elle n'était pas arithmétique puisque les différences de deux termes consécutifs variaient
Re: Résolution équation
C'est mieux d'écrire l'énoncé complet dès le départ, ça évite qu'on travaille sur des interprétations ou des erreurs.
Re: Résolution équation
Bonjour Razes, je veillerai bien à écrire pur l'énoncé la prochaine fois 
Merci pour la correction, pour d) je trouve que Un=(2Vn+1)/(1-Vn)
Mais quand je remplace Vn par 2/5*(-1/2)^n je trouve Un=(1+4/5*(-1/2)^n)/(-2/5*(-1/2)^n+1)
Est-ce que c'est simplifiable ?
Bonne journée
Merci pour la correction, pour d) je trouve que Un=(2Vn+1)/(1-Vn)
Mais quand je remplace Vn par 2/5*(-1/2)^n je trouve Un=(1+4/5*(-1/2)^n)/(-2/5*(-1/2)^n+1)
Est-ce que c'est simplifiable ?
Bonne journée
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 162 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
