Exercice sur l'arithmétique des polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
par jonses » 26 Jan 2014, 10:14
Bonjour,
J'essaye de faire un exercice sur l'arithmétique des polynômes, mais je suis bloqué : je ne vois pas comment utiliser certaines données de l'énoncé :
-
Soit
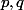
deux entiers naturels premiers entre eux.
Je dois montrer que
(X^q-1))
divise
(X^{pq}-1))
-
En fait je ne vois pas vraiment comment me servir de la donnée "
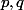
deux entiers naturels premiers entre eux "
Pour aboutir au résultat demandé, je pensais montré que toutes les racines de
)
et de
)
sont des racines de
. Mais je vois pas comment intervient cette donnée de l'énoncé.
Si quelqu'un peut m'expliquer svp.
Je vous remercie d'avance pour vos réponses.
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 26 Jan 2014, 10:37
salut
Tu as
^{q}-1\)=\(X^{p}-1\)(\ ...\ ))
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
par wserdx » 26 Jan 2014, 14:45
L'idée de montrer que les racines de l'un sont aussi racines de l'autre est presque correcte : il faut penser aussi qu'elles aient la même multiplicité (ou plus précisément que la multiplicité dans le premier soit inférieure ou égale à la multiplicité dans le second). Par exemple si p=q, les racines seront doubles dans le premier polynôme, mais pas toutes dans le second.
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 26 Jan 2014, 15:05
on peut montrer que
divise
que
divise aussi
et que le PGCD de
et de
est
-
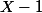
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
par jonses » 26 Jan 2014, 16:08
wserdx a écrit:L'idée de montrer que les racines de l'un sont aussi racines de l'autre est presque correcte : il faut penser aussi qu'elles aient la même multiplicité (ou plus précisément que la multiplicité dans le premier soit inférieure ou égale à la multiplicité dans le second). Par exemple si p=q, les racines seront doubles dans le premier polynôme, mais pas toutes dans le second.
Je pense que j'ai compris où intervient le fait que p et q soient premier entre eux : puisqu'il sont premier entre eux, les racines p-èmes de l'unité à l'excepté de 1 et les racines q-ème de l'unité à l'excepté de 1 sont distinctes.
chan79 a écrit:on peut montrer que
divise
que
divise aussi
et que le PGCD de
et de
est
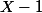
J'ai montré tout ça, mais j'ai pas réussi à aboutir avec...
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 26 Jan 2014, 17:02
jonses a écrit:Je pense que j'ai compris où intervient le fait que p et q soient premier entre eux : puisqu'il sont premier entre eux, les racines p-èmes de l'unité à l'excepté de 1 et les racines q-ème de l'unité à l'excepté de 1 sont distinctes.
J'ai montré tout ça, mais j'ai pas réussi à aboutir avec...
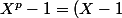 P(X))
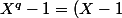 Q(X))
avec
P et Q premiers entre eux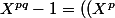^q -1)=(X^p-1)K(X)=(X-1)P(X) K(X))
^p -1)=(X^q-1)H(X)=(X-1)Q(X) H(X))
est divisible par
P(X)Q(X))
donc
, est divisible par
^2P(X)Q(X))
soit
P(X)(X-1)Q(X))
soit
(X^q -1))
à vérifier ...
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 26 Jan 2014, 20:15
Tu peut aussi simplement dire que les racines de
sont les racines p-ièmes et q-ièmes de l'unité qui sont toutes des racinees simples
sauf 1 qui est racine double.
Or ces racines sont aussi racines de
, y compris 1 qui est bien racine double donc le premier polynôme divise le second.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
