Module et argument
17 messages
- Page 1 sur 1
module et argument
Bonsoir,
On me demande de calculer pour a appartient à [0;2pi], le module et si possible, un argument de 1+sin(a)+icos(a).
j'ai fait :
z=1+sin(a)+icos(a)
|z1|²=(1+sin(a))²+(cos(a))²=2(1+sin(a)).
Je me suis arrêtée là car je ne vois pas comment en déduire le module et l'argument
merci de m'expliquer
On me demande de calculer pour a appartient à [0;2pi], le module et si possible, un argument de 1+sin(a)+icos(a).
j'ai fait :
z=1+sin(a)+icos(a)
|z1|²=(1+sin(a))²+(cos(a))²=2(1+sin(a)).
Je me suis arrêtée là car je ne vois pas comment en déduire le module et l'argument
merci de m'expliquer
pluie2 a écrit:Bonsoir,
On me demande de calculer pour a appartient à [0;2pi], le module et si possible, un argument de 1+sin(a)+icos(a).
j'ai fait :
z=1+sin(a)+icos(a)
|z1|²=(1+sin(a))²+(cos(a))²=2(1+sin(a)).
Je me suis arrêtée là car je ne vois pas comment en déduire le module et l'argument
merci de m'expliquer
Ce qu'a écrit carpate, c'est uniquement la formule générale (pour z quelconque non nul) : 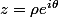 où
où  est le module de
est le module de  et
et  un argument de
un argument de  .
.
Mais il s'est un peu trompé vu que le module que tu as trouvé, c'est)}) donc il aurais du écrire
donc il aurais du écrire )}e^{i\theta}) .
.
En divisant le z (que tu connais) par le module de z (que tu as calculé), ça te permet de voir combien valent) et
et ) .
.
Mais en fait, cette méthode qui marche souvent (assez) bien n'est pas adaptée dans le cas présent : tu va tomber sur des calculs lourds et compliqués.
Ici, il y a une "astuce" :
En général, lorsque z1 et z2 sont deux complexe dont on connait le module et un argument, on a très facilement le module et un argument du produit z1 x z2 ce sont ...
Par contre il est difficile d'avoir le module et l'argument de la somme z1 + z2.... SAUF si z1 et z2 sont de même module.
Fait un dessin ou tu représente deux complexes de même module et d'arguments respectifs et
et  puis trace sur le même dessin le point z1+z2.
puis trace sur le même dessin le point z1+z2.
Quelle figure as-tu sous les yeux ? Peut tu en déduire un argument de z1+z2 ?
Application : le z de ton exercice est la somme de 1 et de cos(a)+i.sin(a) qui sont de même module...
Mais il s'est un peu trompé vu que le module que tu as trouvé, c'est
En divisant le z (que tu connais) par le module de z (que tu as calculé), ça te permet de voir combien valent
Mais en fait, cette méthode qui marche souvent (assez) bien n'est pas adaptée dans le cas présent : tu va tomber sur des calculs lourds et compliqués.
Ici, il y a une "astuce" :
En général, lorsque z1 et z2 sont deux complexe dont on connait le module et un argument, on a très facilement le module et un argument du produit z1 x z2 ce sont ...
Par contre il est difficile d'avoir le module et l'argument de la somme z1 + z2.... SAUF si z1 et z2 sont de même module.
Fait un dessin ou tu représente deux complexes de même module et d'arguments respectifs
Quelle figure as-tu sous les yeux ? Peut tu en déduire un argument de z1+z2 ?
Application : le z de ton exercice est la somme de 1 et de cos(a)+i.sin(a) qui sont de même module...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
j'ai quelques petites questions :
a) par la méthode de carpate, comment je fais pour en déduire cos(a) et sin (a) désolé malgré votre explication je ne vois pas trop, faut il que je divise z=rac(2(1+sin(a))e^ia) par p ?
b) pour votre méthode: je n'ai qu'un z et pas deux donc comment pouvoir l'utiliser ?
a) par la méthode de carpate, comment je fais pour en déduire cos(a) et sin (a) désolé malgré votre explication je ne vois pas trop, faut il que je divise z=rac(2(1+sin(a))e^ia) par p ?
b) pour votre méthode: je n'ai qu'un z et pas deux donc comment pouvoir l'utiliser ?
La méthode "de carpate" (qui marche en général bien dans des exercices "de base"), ca consiste à écrire au départ :
+i\cos(a)=\rho e^{i\theta}=\rho\Big(\cos(\theta)+i\sin(\theta) \Big))
On connait z et veut évaluer le module et un des arguments
et un des arguments  .
.
Pour le module , pas de soucis :
, pas de soucis :
)^2+\cos^2(a)}=\sqrt{2+2\sin(a)})
Et pour trouver un argument , ben on écrit que
, ben on écrit que
+i\sin(\theta)=\frac{z}{\rho}=\frac{1+\sin(a)}{\sqrt{2+2\sin(a)}}+i\frac{\cos(a)}{\sqrt{2+2\sin(a)}})
Donc on cherche tel que :
tel que :
=\frac{1+\sin(a)}{\sqrt{2+2\sin(a)}})
et
=\frac{\cos(a)}{\sqrt{2+2\sin(a)}})
Arrivé là, on pourrait dire qu'on a fini l'exo vu qu'à priori, on voit pas trop comment simplifier les fractions et qu'on voit pas du tout quel va marcher...
va marcher...
C'est pour ça que je te proposait de... faire autre chose... (dans le cas particulier de cet exercice)
b) Et concernant la méthode que je te suggérais, tu as bien deux complexes que tu ajoute : le premier, c'est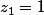 et le deuxième, c'est
et le deuxième, c'est +i\sin(a)) .
.
Donc je le (re)dit : trace sur un même dessin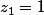 ,
, +i\sin(a)) (en prenant pour a un angle "le plus quelconque possible") ainsi que
(en prenant pour a un angle "le plus quelconque possible") ainsi que  .
.
Normalement, on "lit" directement sur le dessin un des arguments de (je pense que c'est niveau collège)
(je pense que c'est niveau collège)
On connait z et veut évaluer le module
Pour le module
Et pour trouver un argument
Donc on cherche
et
Arrivé là, on pourrait dire qu'on a fini l'exo vu qu'à priori, on voit pas trop comment simplifier les fractions et qu'on voit pas du tout quel
C'est pour ça que je te proposait de... faire autre chose... (dans le cas particulier de cet exercice)
b) Et concernant la méthode que je te suggérais, tu as bien deux complexes que tu ajoute : le premier, c'est
Donc je le (re)dit : trace sur un même dessin
Normalement, on "lit" directement sur le dessin un des arguments de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
pluie2 a écrit:Bonsoir,
On me demande de calculer pour a appartient à [0;2pi], le module et si possible, un argument de 1+sin(a)+icos(a).
merci de m'expliquer
si
on distingue trois cas pour déterminer Arg(z)
cas 1
deux fois le cosinus est positif, c'est
cas 2
le cosinus est négatif, on rajoute
cas 3
et effectivement, le cas où
dans ce cas,
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
