@Dacu,
x^4+2ix^3+3x^2+4ix+5<0
1) tu dis que x est complexe.
2) ton inéquation n'existe que si le nombre x^4+2ix^3+3x^2+4ix+5 appartient à R.
3) Première étape: tu cherches l'ensemble des x tels que x^4+2ix^3+3x^2+4ix+5 appartient à R.
3.1) tu poses x= a+ib, avec a appartient à R, b appartient à R.
3.2) tu injectes dans (3), et tu cherches a et b, tels que la partie imaginaire de x^4+2ix^3+3x^2+4ix+5 soit nulle.
qu'obtiens-tu?
Les inéquations
32 messages
- Page 2 sur 2 - 1, 2
Certes, 3x² + 4ix + 5 est réel si x est imaginaire pur.
x imaginaire pur est une condition suffisante mais pas nécessaire pour que 3x² + 4ix + 5 soit réel.
Contre exemple : x = 2 - (2/3).i entraîne aussi que 3x² + 4ix + 5 est réel.
On peut facilement montrer que x = a - (2/3).i avec a réel quelconque conduit aussi à "3x² + 4ix + 5" réel.
Par "chance", cette voie conduit à 3x² + 4ix + 5 positif et donc il n'y a pas de solution, dans cette voie pour 3x² + 4ix + 5 < 0. (coup de bol).
N'empêche, on ne peut pas se contenter d'étudier les solutions avec x imaginaire pur, se serait risquer très largement de louper des solutions.
*****
J'aurais fait ceci :
Pour l'étude de 3x² + 4ix + 5 < 0 :
Posons : x = a+ib
3x² + 4ix + 5 = 3(a²-b²+2iab) + 4ai-4b + 5
3x² + 4ix + 5 = 3(a²-b²)-4b + 5 + 6iab + 4ai
3x² + 4ix + 5 = 3a² - 3b² -4b + 5 + 2i(2a + 3ab)
Pour que 3x² + 4ix + 5 soit réel alors, il faut que :
2a + 3ab = 0
soit a = 0, soit b = -2/3
1°)
Si b = -2/3
x = a - (2/3)i
3x² + 4ix + 5 = 3a² - 4/3 + 8/3 + 5 = 3a² + 19/3 ... qui ne peut pas être < 0. (mais si on avait demandé par exemple 3x² + 4ix + 5 > 0 ou bien 3x² + 4ix + 5 > 12 ou ... alors cette voie aurait donné des solutions).
2°)
Si a = 0
x = ib
3x² + 4ix + 5 = - 3b² - 4b + 5 = -(3b² + 4b - 5) ... qui est < 0 pour b dans ]- oo ; (-2 - V19)/3[ U ](-2 + V19)/3 ; +oo[
Donc x = i.b avec b dans ]- oo ; (-2 - V19)/3[ U ](-2 + V19)/3 ; +oo[ convient.
*****
Pour ne pas louper des solutions, il faut partir de x = a + ib et pas de x = i.b
Pareil évidemment pour étudier x^4+2ix^3+3x^2+4ix+5<0
:zen:
x imaginaire pur est une condition suffisante mais pas nécessaire pour que 3x² + 4ix + 5 soit réel.
Contre exemple : x = 2 - (2/3).i entraîne aussi que 3x² + 4ix + 5 est réel.
On peut facilement montrer que x = a - (2/3).i avec a réel quelconque conduit aussi à "3x² + 4ix + 5" réel.
Par "chance", cette voie conduit à 3x² + 4ix + 5 positif et donc il n'y a pas de solution, dans cette voie pour 3x² + 4ix + 5 < 0. (coup de bol).
N'empêche, on ne peut pas se contenter d'étudier les solutions avec x imaginaire pur, se serait risquer très largement de louper des solutions.
*****
J'aurais fait ceci :
Pour l'étude de 3x² + 4ix + 5 < 0 :
Posons : x = a+ib
3x² + 4ix + 5 = 3(a²-b²+2iab) + 4ai-4b + 5
3x² + 4ix + 5 = 3(a²-b²)-4b + 5 + 6iab + 4ai
3x² + 4ix + 5 = 3a² - 3b² -4b + 5 + 2i(2a + 3ab)
Pour que 3x² + 4ix + 5 soit réel alors, il faut que :
2a + 3ab = 0
soit a = 0, soit b = -2/3
1°)
Si b = -2/3
x = a - (2/3)i
3x² + 4ix + 5 = 3a² - 4/3 + 8/3 + 5 = 3a² + 19/3 ... qui ne peut pas être < 0. (mais si on avait demandé par exemple 3x² + 4ix + 5 > 0 ou bien 3x² + 4ix + 5 > 12 ou ... alors cette voie aurait donné des solutions).
2°)
Si a = 0
x = ib
3x² + 4ix + 5 = - 3b² - 4b + 5 = -(3b² + 4b - 5) ... qui est < 0 pour b dans ]- oo ; (-2 - V19)/3[ U ](-2 + V19)/3 ; +oo[
Donc x = i.b avec b dans ]- oo ; (-2 - V19)/3[ U ](-2 + V19)/3 ; +oo[ convient.
*****
Pour ne pas louper des solutions, il faut partir de x = a + ib et pas de x = i.b
Pareil évidemment pour étudier x^4+2ix^3+3x^2+4ix+5<0
:zen:
Black Jack a écrit:Certes, 3x² + 4ix + 5 est réel si x est imaginaire pur.
x imaginaire pur est une condition suffisante mais pas nécessaire pour que 3x² + 4ix + 5 soit réel.
Contre exemple : x = 2 - (2/3).i entraîne aussi que 3x² + 4ix + 5 est réel.
On peut facilement montrer que x = a - (2/3).i avec a réel quelconque conduit aussi à "3x² + 4ix + 5" réel.
Par "chance", cette voie conduit à 3x² + 4ix + 5 positif et donc il n'y a pas de solution, dans cette voie pour 3x² + 4ix + 5 0 ou bien 3x² + 4ix + 5 > 12 ou ... alors cette voie aurait donné des solutions).
2°)
Si a = 0
x = ib
3x² + 4ix + 5 = - 3b² - 4b + 5 = -(3b² + 4b - 5) ... qui est < 0 pour b dans ]- oo ; (-2 - V19)/3[ U ](-2 + V19)/3 ; +oo[
Donc x = i.b avec b dans ]- oo ; (-2 - V19)/3[ U ](-2 + V19)/3 ; +oo[ convient.
*****
Pour ne pas louper des solutions, il faut partir de x = a + ib et pas de x = i.b
Pareil évidemment pour étudier x^4+2ix^3+3x^2+4ix+5<0
:zen:
Correctement,mais mon raisonnement est beaucoup plus simple!S'il vous plaît lire mes messages !
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
tu es évidemment autorisé à développer tes pistes de réflexions.
Maintenant:
- si tu demandes de l'aide pour résoudre ton problème on t'a déjà donné toutes les billes en main
- si tu veux faire vérifier ta méthode, alors je comprends personnellement pas pourquoi faire intervernir a.
- si tu nous mets au défi de trouver les solutions de ton inéquation, tu comprendras qu'on ne te répond pas parce que ca n'éveille pas grand intérêt.
Dans tous les cas, il aurait été appréciable que tu poses clairement ta question.
Maintenant:
- si tu demandes de l'aide pour résoudre ton problème on t'a déjà donné toutes les billes en main
- si tu veux faire vérifier ta méthode, alors je comprends personnellement pas pourquoi faire intervernir a.
- si tu nous mets au défi de trouver les solutions de ton inéquation, tu comprendras qu'on ne te répond pas parce que ca n'éveille pas grand intérêt.
Dans tous les cas, il aurait été appréciable que tu poses clairement ta question.
la vie est une fête 
Dacu a écrit:Correctement,mais mon raisonnement est beaucoup plus simple!S'il vous plaît lire mes messages !
Peut-être, mais il ne mêne nulle part.
Pour ma part, en une dizaine de lignes, je trouve qu'on doit avoir : x = a + ib
avec a = racinecarrée[(b+2)*(b-1)] et b dans ]-oo ; -2,034961...[ U ]1,034961... ; +oo[
Essaie donc avec ta méthode.
:zen:
Dacu a écrit:Je le répète :
Avec mon raisonnement sont calculées rapide les solutions de l'inéquationqui peut s'écrire
où
est un nombre réel et
,et puis, il s'ensuit
et evidemment les solutions de l'inéquation
sont
et
.
Oui, avec comme remarques :
- L'usage du signe radical est réservé aux réels positifs (mais personnellement cela m'est égal).
- La méthode ne peut s'appliquer qu'à des cas particuliers.
Comment faire avec la dite méthode par exemple pour x^4 + 7ix³ - 3x² + 5ix - 2 < 0 ?
:zen:
Bonjour!
L'inéquation proposée par vous est plus difficile à résoudre même si nous supposons que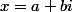 .L'inéquation de degré 4 proposé par moi que j'ai dessiné pour être en mesure de résoudre plus facilement.Comment résoudre l'inéquation de degré 4 proposé par vous avec la solution du type
.L'inéquation de degré 4 proposé par moi que j'ai dessiné pour être en mesure de résoudre plus facilement.Comment résoudre l'inéquation de degré 4 proposé par vous avec la solution du type 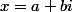 ?
?
Cordielement!
L'inéquation proposée par vous est plus difficile à résoudre même si nous supposons que
Cordielement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Dacu a écrit:Bonjour!
L'inéquation proposée par vous est plus difficile à résoudre même si nous supposons que.L'inéquation de degré 4 proposé par moi que j'ai dessiné pour être en mesure de résoudre plus facilement.Comment résoudre l'inéquation de degré 4 proposé par vous avec la solution du type
?
Cordielement!
Comme cela a été indiqué dans de nombreux messages dans ce topic.
On remplace x par a + ib dans " x^4 + 7ix³ - 3x² + 5ix - 2"
On développe le tout pour le mettre sous la forme : x^4 + 7ix³ - 3x² + 5ix - 2 = A + i.B
Avec évidemment A et B étant des fonctions réelles des réels a et b
On a alors le système suivant à résoudre :
B = 0
A < 0
Ce n'est pas forcément facile, mais on est déjà débarassé des complexes pour poursuivre.
C'est calculatoire et peut-être ennuyeux, mais ta méthode présume qu'on puisse trouver une manière "spéciale" d'écrire l'équation qui arrange bien les choses et ce n'est pas gagné d'avance (comme dans cet exemple).
Je n'ai pas essayé de voir où on aboutissait avec la méthode préconisée par beaucoup dans le cas de l'inéquation x^4 + 7ix³ - 3x² + 5ix - 2 < 0.
... Il y a en tout cas au moins la solution x = 0 qui convient. :happy2:
:zen:
32 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
