Partie fermé dans espace fonction continue et bornée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mysterion
- Membre Relatif
- Messages: 117
- Enregistré le: 30 Jan 2012, 14:15
-
 par Mysterion » 18 Fév 2013, 14:54
par Mysterion » 18 Fév 2013, 14:54
Salut,
Dans l'ensemble

des fonction de IR dans IR continue et bornée, munie de la norme infinie

, j'essaye de savoir si le sous ensemble
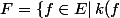=sup_{(x,y)} \frac{|f(x)-f(y)|}{|x-y|} < \infty \})
est un fermé.
Je vois deux options :
1. l'image réciproque d'un fermé d'une application continue est un fermé. Mais pour qu'elle application continue de E vers...?
2. Ou je montre que l'adhérence de F c'est F lui même. Et que pour tout f de E limite d'une suite de F,
k(f) est fini. Mais avec
)
j'avance pas.
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 18 Fév 2013, 17:56
par DamX » 18 Fév 2013, 17:56
[quote="Mysterion"]Salut,
Dans l'ensemble

des fonction de IR dans IR continue et bornée, munie de la norme infinie

, j'essaye de savoir si le sous ensemble [TEX]F=\{ f \in E | \, k(f)=sup_{(x,y)} \frac{|f(x)-f(y)|}{|x-y|} 1/n.
fn est bien continue et bornée.
Et tu as évidemment k(f) = n, la fonction limite (un créneau) n'est pas vraiment dans l'ensemble..
Damien
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 18 Fév 2013, 18:53
par Doraki » 18 Fév 2013, 18:53
Si tu veux montrer qu'il n'est pas fermé il vaut mieux choisir une suite qui converge dans E mais dont la limite n'est pas dans F (qui fait des pentes arbitrairement grandes).
Par exemple fn(x) = sin(e^x)/x pour x entre ln(pi) et ln(n*pi), et 0 ailleurs, est dans F.
Cette suite converge dans E vers la fonction f(x) = sin(e^x)/x pour x >= ln(pi) et 0 ailleurs, qui n'est pas dans F.
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 18 Fév 2013, 19:03
par DamX » 18 Fév 2013, 19:03
Doraki a écrit:Si tu veux montrer qu'il n'est pas fermé il vaut mieux choisir une suite qui converge dans E mais dont la limite n'est pas dans F (qui fait des pentes arbitrairement grandes).
Par exemple fn(x) = sin(e^x)/x pour x entre ln(pi) et ln(n*pi), et 0 ailleurs, est dans F.
Cette suite converge dans E vers la fonction f(x) = sin(e^x)/x pour x >= ln(pi) et 0 ailleurs, qui n'est pas dans F.
Oui en effet, en voulant trop simplifier, ma suite de fonctions ne convergeait pas dans E (et ne convergeait en fait Meme pas vers le créneau au sens de la norme infinie). L'idée était bien de rechercher une pente qui part à l'infini. Ton exemple est mieux.
Damien
-
Mysterion
- Membre Relatif
- Messages: 117
- Enregistré le: 30 Jan 2012, 14:15
-
 par Mysterion » 19 Fév 2013, 20:44
par Mysterion » 19 Fév 2013, 20:44
merci pour vos réponses.
En fait le problème était plus simple que ça, j'ai manqué quelques éléments. En fait F n'est pas muni de la norme infinie mais d'une autre norme spécifique, et qui rend l'espace F complet. On a donc un espace complet inclus dans un espace complet. Donc F est fermé.
Cependant j'aimerais bien savoir d'où provient cette propriété sur les ouverts:
Si tu veux montrer qu'il n'est pas fermé il vaut mieux choisir une suite qui converge dans E mais dont la limite n'est pas dans F
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Fév 2013, 21:10
par Doraki » 19 Fév 2013, 21:10
c'est la définition de ne pas être fermé dans un espace métrique E.
La limite de cette suite est point de F et tu n'as pas de voisinage de ce point qui n'intersecte pas E puisque tu as une suite de E qui converge vers F. Donc ce point n'est pas dans l'intérieur de E\F, donc E\F n'est pas ouvert donc F n'est pas fermé. (et ce sont des équivalences faciles partout)
-
Mysterion
- Membre Relatif
- Messages: 117
- Enregistré le: 30 Jan 2012, 14:15
-
 par Mysterion » 19 Fév 2013, 22:55
par Mysterion » 19 Fév 2013, 22:55
Doraki a écrit:c'est la définition de ne pas être fermé dans un espace métrique E.
La limite de cette suite est point de F et tu n'as pas de voisinage de ce point qui n'intersecte pas E puisque tu as une suite de E qui converge vers F. Donc ce point n'est pas dans l'intérieur de E\F, donc E\F n'est pas ouvert donc F n'est pas fermé. (et ce sont des équivalences faciles partout)
Ok, merci bien
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
