Bonjour
Soit E={polynomes de C[X]verifiant P'/P}.
Il est clair que les polynomes proportionnels à (X-a)^n sont dans E.
Comment montrer que tt polynome dans E est de cette forme?
Merci
Polynomes verifiant P'/P
5 messages
- Page 1 sur 1
je ne connais pas ce C[X]
mais si polynomes de C[X] sont les meme plynomes que j'ai vu en terminal
et si p'/p : p(x)=q(x)p'(x)
alors voila tt ce que je peux faire pour toi
=\bigsum_{k=0}^{n}a_kx^k)
=\bigsum_{k=0}^{n-1}(k+1)a_{k+1}x^k)
=bx+c)
si on pendre p(x)=q(x)p'(x)
alors on trouve quea_{k+1}+bka_k) pour k de {0,1,2,...,n-1}
pour k de {0,1,2,...,n-1}
donc}a_{k})
/n][1-(k-2)/n][1-(k-3)/n]...[1-1/n]}{c^{k-1}k!}a_1=a_0\frac{[n-(k-1)][n-(k-2)][n-(k-3)]...[n-1]}{c^{k}n^{k-1}k!}=a_0\frac{C_{n}^{k}}{c^{k}n^{k}})
^k)
donc=\frac{a_0}{(cn)^n}(cn+x)^n)
et puisque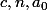 sont des valeur fixes qui ne varie pas.
sont des valeur fixes qui ne varie pas.
alors) s'ecrit ous la forme
s'ecrit ous la forme ^n)
et puisque kp(x) est aussi une solution quelque soit k
alors=B\times\frac{k}{B}(x+A)^n=k(x+A)^n)
mais si polynomes de C[X] sont les meme plynomes que j'ai vu en terminal
et si p'/p : p(x)=q(x)p'(x)
alors voila tt ce que je peux faire pour toi
si on pendre p(x)=q(x)p'(x)
alors on trouve que
etdonc b=1/n
donc
donc
et puisque
alors
et puisque kp(x) est aussi une solution quelque soit k
alors
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
