Propriété des matrices

par **Dante0** » 05 Nov 2012, 23:57

XENSECP a écrit:Non. J'aime pas donner des indications qui sont contestées alors même que tu n'as pas de pistes.

J'ai pas contesté, j'ai dit que je ne voyais pas où tu voulais en venir, en gros j'ai pas compris quoi...

par **Dante0** » 06 Nov 2012, 16:28

Up..... :cry:

par **Dante0** » 08 Nov 2012, 11:34

:help: :help::help::help:

par **Dante0** » 09 Nov 2012, 13:36

Up !! :doh: :doh: :doh:

par **guiguipelloq** » 10 Nov 2012, 11:02

Bon comme je l'ai dit, tu connais des solutions candidates pour résoudre AX=0 (celles de BAX=0)... Eh bien, essaye-les !

par **Dante0** » 10 Nov 2012, 12:47

guiguipelloq a écrit:Bon comme je l'ai dit, tu connais des solutions candidates pour résoudre AX=0 (celles de BAX=0)... Eh bien, essaye-les !

Donc en fait le nombre de solutions d'AX=0 est égal au nombre de solutions de BAX=0 ?
C'est pas plus simple de résoudre AX=0 ? Pourquoi passer par BAX=0 ?

par **guiguipelloq** » 10 Nov 2012, 13:02

Tu as un certain nombre de candidates pour AX=0 : vérifie quelles sont celles qui conviennent, et déduis-en toute les solutions de AX=0, puis compte-les.

par **Dante0** » 10 Nov 2012, 13:11

guiguipelloq a écrit:Tu as un certain nombre de candidates pour AX=0 : vérifie quelles sont celles qui conviennent, et déduis-en toute les solutions de AX=0, puis compte-les.

AX=0 a pour unique solution x=y=z=0

par **guiguipelloq** » 10 Nov 2012, 13:34

Bon ça m'a l'air bien brumeux tout ça... J'ai repris l'énoncé et je trouve une infinité de solutions pour les deux systèmes. Çe ne remet pas en cause ce qu'on a dit, mais ça pose un problème pour l'énoncé.
Donc d'ailleurs, AX=0 n'a pas que cette solution. Ses solutions sont tous les triplets (x,y,z) tels que x=z, y=-(3/2)z, z=z. Ils s'écrivent sous la forme z*(1,(-3/2),1). Par exemple; pour z=1, le triplet x=1, y=(-3/2) et z=1 fonctionne.

par **Dante0** » 10 Nov 2012, 14:09

guiguipelloq a écrit:Bon ça m'a l'air bien brumeux tout ça... J'ai repris l'énoncé et je trouve une infinité de solutions pour les deux systèmes. Çe ne remet pas en cause ce qu'on a dit, mais ça pose un problème pour l'énoncé.
Donc d'ailleurs, AX=0 n'a pas que cette solution. Ses solutions sont tous les triplets (x,y,z) tels que x=z, y=-(3/2)z, z=z. Ils s'écrivent sous la forme z*(1,(-3/2),1). Par exemple; pour z=1, le triplet x=1, y=(-3/2) et z=1 fonctionne.

Ok j'ai compris, j'ai repéré mon erreur.
Comment conclure quant au nombre de solution de AX=0 ? Une infinité apparemment non ?

par **guiguipelloq** » 10 Nov 2012, 14:14

Oui, mais bon... l'infini n'est pas un nombre, donc je trouve l'énoncé assez mal posé. Au passage, tu es en quelle classe ?

par **Dante0** » 10 Nov 2012, 14:36

guiguipelloq a écrit:Oui, mais bon... l'infini n'est pas un nombre, donc je trouve l'énoncé assez mal posé. Au passage, tu es en quelle classe ?

2e année fac d'eco.
Ce que je trouve curieux c'est qu'après avoir calculé BA on nous demande d'en déduire le nombre de solutions de AX=0, normalement ca suppose un lien logique direct donc pas besoin de calculs...

par **guiguipelloq** » 10 Nov 2012, 14:53

C'est vrai. Les solutions de BAX=0 sont également infinies mais comme on l'a dit, il peut y avoir un nb infini de candidats pour un nb fini de solutions réelles. J'ai aussi un peu de mal à comprendre. Peut-être faudrait-il déplacer le topic (ou en ouvrir un nouveau) dans la section supérieur.

par **Dante0** » 11 Nov 2012, 11:39

guiguipelloq a écrit:C'est vrai. Les solutions de BAX=0 sont également infinies mais comme on l'a dit, il peut y avoir un nb infini de candidats pour un nb fini de solutions réelles. J'ai aussi un peu de mal à comprendre. Peut-être faudrait-il déplacer le topic (ou en ouvrir un nouveau) dans la section supérieur.

Ok merci !

Qu'en est-il de ma 2e question concernant la matrice N ? Ca a l'air simple, je suis frustré de ne pas avoir réussi. :mur:

par **Backtrack** » 11 Nov 2012, 14:38

Hello ,

Ecris ton système de manière matricielle de façon à faire apparaître la matrice N . Ensuite essaie de faire apparaître N^2 ( si on fait ça c'est juste pour facilité la lecture des solutions je pense )

par **Dante0** » 11 Nov 2012, 15:33

J'arrive pas à écrire la matrice en Latex :doh:
Pourquoi calculer N² ?

par **Backtrack** » 11 Nov 2012, 19:18

Une fois que t'as écris ton système sous forme matricielle, multiplie par N de chaque coté

par **Dante0** » 11 Nov 2012, 19:47

Backtrack a écrit:Une fois que t'as écris ton système sous forme matricielle, multiplie par N de chaque coté

On me demande de calculer

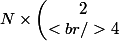
Pourquoi tu me demandes de calculer

?
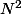
J'avais pas écrit en Latex désolé ^^' mais c'etait pas un exposant

Quand je fais ce calcul je n'arrive pas à en déduire la solution du système plus haut.. :/

par **Backtrack** » 11 Nov 2012, 20:46

Oui oui je sais mais ton système donne :

N*(x,y)=(2,4) ( avec (2,4) matrice colonne enfin on se comprend! )

Si tu multiplie par N de chaque coté :

N^2 *(x,y)=N*(2,4) ( c'est ce qu'on t'as fait calculer avant )

Et N^2 est diagonale donc t'en déduis direct x et y

par **Dante0** » 11 Nov 2012, 22:12

Backtrack a écrit:Oui oui je sais mais ton système donne :

N*(x,y)=(2,4) ( avec (2,4) matrice colonne enfin on se comprend! )

Si tu multiplie par N de chaque coté :

N^2 *(x,y)=N*(2,4) ( c'est ce qu'on t'as fait calculer avant )

Et N^2 est diagonale donc t'en déduis direct x et y

Edit : J'ai compris merci pour l'aide !

Propriété des matrices

Qui est en ligne