Somme d'une série de fonctions par comparaison à une intégra
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 05 Nov 2012, 17:54
par Wenneguen » 05 Nov 2012, 17:54
Bonjour,
je sais qu'on peut comparer une série numérique à une intégrale afin d'en déterminer la somme dans certains cas
( Cf.
http://fr.wikipedia.org/wiki/Comparaison_s%C3%A9rie-int%C3%A9grale#Principe_de_base, " Principe de base " ).
Cependant j'ai du mal à adapter la méthode dans le cas d'une série de fonctions, pourriez-vous me guider ? En particulier je travaille sur la série
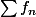
avec

sur

.
Merci de votre aide ! :we:
Edit : je crois avoir compris que ma question est plutôt stupide dans la mesure où le x joue simplement le rôle d'une constante... :marteau:
Edit 2 : Finalement non j'y arrive pas :mur:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Nov 2012, 20:02
par fatal_error » 05 Nov 2012, 20:02
slt,
Soit f telle que un=f(n). Si f est décroissante et continue sur l'intervalle [0, \infty[, alors on peut encadrer
 = \frac{1}{n+n^2x^2}\\<br />u_n = f(n))
(note f ne dépend que de n, x se comporte comme
paramètre)
donne
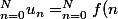 = \bigsum_{n=0}^{N} \frac{1}{n+n^2x^2} \leq u_0 + \bigint_0^N f(t)dt)
avec
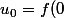 = \frac{1}{0+0})
donc déjà, tu as le droit de commencer à n=1.

en supposant que t'as les bons indices...il te reste à calculer
dt = \bigint \frac{1}{t+t^2x^2}dt = \frac{1}{x^2}\bigint \frac{1}{(t+\frac{1}{2x^2})^2 - \frac{1}{x^4}}dt...)
etc puis changement arctan et tout le tatouin.
il faut comme tu le constates également faire gaffe au cas x=0
la vie est une fête

-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 05 Nov 2012, 20:05
par Wenneguen » 05 Nov 2012, 20:05
fatal_error a écrit:slt,
 = \frac{1}{n+n^2x^2}\\<br />u_n = f(n))
(note f ne dépend que de n, x se comporte comme
paramètre)
donne
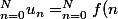 = \bigsum_{n=0}^{N} \frac{1}{n+n^2x^2} \leq u_0 + \bigint_0^N f(t)dt)
avec
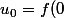 = \frac{1}{0+0})
donc déjà, tu as le droit de commencer à n=1.

en supposant que t'as les bons indices...il te reste à calculer
dt = \bigint \frac{1}{t+t^2x^2}dt = \frac{1}{x^2}\bigint \frac{1}{(t+\frac{1}{2x^2})^2 - \frac{1}{x^4}}dt...)
etc puis changement arctan et tout le tatouin.
il faut comme tu le constates également faire gaffe au cas x=0
Ok merci, ouais en fait le x change pas grand chose

D'ailleurs c'est plus simple de calculer l'intégrale par décomposition en éléments simples que par une arctan il me semble... :zen:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Nov 2012, 20:11
par fatal_error » 05 Nov 2012, 20:11
ouais je te crois ca commence à remonter un peu pour moi :cry:
la vie est une fête

-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 05 Nov 2012, 20:26
par Wenneguen » 05 Nov 2012, 20:26
En fait j'y arrive toujours pas x) Comme primitive je trouve -ln(1+x^2*t)+ln(t) et en la faisant varier de 1 à l'infini :
)
Le problème c'est qu'en testant avec maple la somme des 500 premiers termes pour x=2 par exemple, je trouve un truc différent de
)
:triste:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Nov 2012, 20:56
par fatal_error » 05 Nov 2012, 20:56
ya pas écrit que yavait l'égalité mais l'inégalité.
A mon avis (si tu calcules u1 tu dois avoir genre 1/5)
tu devrais avoir ta somme de 200 termes comprise entre
ln(5/4) et 1/5+ln(5/4)
la vie est une fête

-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 05 Nov 2012, 21:11
par Wenneguen » 05 Nov 2012, 21:11
fatal_error a écrit:ya pas écrit que yavait l'égalité mais l'inégalité.
A mon avis (si tu calcules u1 tu dois avoir genre 1/5)
tu devrais avoir ta somme de 200 termes comprise entre
ln(5/4) et 1/5+ln(5/4)
Donc pas moyen de trouver la valeur exacte de la fonction somme de la série ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Nov 2012, 21:21
par fatal_error » 05 Nov 2012, 21:21
de cette manière je pense pas, mais ya ptet moyen avec les sommes de riemann ou fourier
la vie est une fête

-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Nov 2012, 21:40
par Pythales » 05 Nov 2012, 21:40
fatal_error a écrit:de cette manière je pense pas, mais ya ptet moyen avec les sommes de riemann ou fourier
La série est sommable si x=1
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
