Soient leurs affixes respectives a, b et c. On a
Montrer que "ABC équilatéral" est équivalent à
Bonne chance, vous en aurez besoin.
Soient a,b,c de module 1 et on suppose que. Montrer que l'un des trois complexe vaut 1.
Montrer qu'un triangle équilatéral ABC vérifie avec ses affixes l'égalité suivante :avec
Kikoo <3 Bieber a écrit:Non, le magicien c'est mon colleurUn jeune homme très gentil.
:p Je ferai le reste avec plaisir mon Benekire.
benekire2 a écrit:Le triangle abc est équilatéral si et seulement si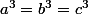
Matt_01 a écrit:D'où ca sort ?
C'est faux dans le cas général, donc tu utilises déjà l'hypothèse de normes égales.
En fait faudrait savoir d'où on part pour la définition de l'équitéral, celle avec les angles permet rapidement d'établir tes égalités, mais c'est moins évident avec les distances.
Kikoo <3 Bieber a écrit:au plan d'Argand-Cauchy.
Kikoo <3 Bieber a écrit:Par truandage tu supposes magie/trucage non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :